Экзаменационные вопросы

1. Основные операции алгебры логики. Функциональная полная система логических элементов. Примеры.

Базовыми элементами, которыми оперирует алгебра логики, являются высказывания. Высказывания строятся над множеством {B, , , , 0, 1}, где B — непустое множество, над элементами которого определены три операции:

отрицание (унарная операция),

конъюнкция (бинарная),

дизъюнкция (бинарная),

а также константы — логический ноль 0 и логическая единица 1.

Дизъю́нкт — пропозициональная формула, являющаяся дизъюнкцией одного или более литералов (например ). Конъюнкт — пропозициональная формула, являющаяся конъюнкцией одного или более литералов (например ).

2. Способы задания булевых функций: СДНФ и СКНФ булевых функций

Способы задания булевых функций

Способы задания булевых функций не отличаются от способов задания обычных функций анализа. К таковым способам задания стандартно относятся:

1) Табличный;

2) Графический;

3) Аналитический.

(1) Табличный способ задания

Пусть w=f(x1,x2,…,xn) — булева функция n аргументов. Область определения данной функции можно рассматривать и как множество упорядоченных наборов (или векторов, или двоичных наборов) D={x1,x2,…,xn | xi ∈ {0,1}, i=1,2,…,n}, на каждом из которых функция принимает одно из двух значений: w ∈ {0,1}. Количество таких наборов (x1,x2,…,xn), согласно правилу прямого произведения, равно |D|=

В качестве примера рассмотрим табличное представление булевой функции трех аргументов w=f(x,y,z), где w,x,y,z ∈ {0,1}. Область определения функции — это множество двоичных наборов D={(x,y,z), | x,y,z ∈ {0,1}}. Их число есть |D|=2^3=8, а количество таких функций равно 2^|D|=2^2^3=256. Значения функции f(x,y,z) удобно представить в виде табл. 1.3, где перечислены всевозможные наборы из нулей и единиц длины 3 и для каждогонабора указано значение функции fi ∈ {0,1} на этом наборе.

В таблицах, аналогичных табл. 1.3 обычно употребляется расположение наборов, соответствующих порядку естественного роста двоичных чисел 0,1,…2^n-1, в

примере n=3.

Определение. Таблицы значений булевых функций, подобные табл. 1.3, называются таблицами истинности булевых функций. Название таблиц происходит от интерпретации значений 1 — истина (TRUE), 0 — ложь (FALSE).

(2) Графический способ задания

Рассмотрим графическое представление булевой функции трех аргументов w=f(x,y,z), заданной таблично (табл. 1.3). Заметим, что множество наборов области определения функции D={(x,y,z) , | x,y,z ∈ {0,1}} является множеством координат точек вершин единичного трехмерного куба (рис. 1.2). Очевидный способ графического представления булевой функции — это отметить каким-то образом вершины куба, в которых функция принимает значение 1. Именно так на рис. 1.2 и сделано. В соответствии с таблицей значений (табл. 1.3) отмечены вершины, в которых булева функция равна 1.

Замечание. Очевидно, что область определения булевой функции n аргументов w=f(x1,x2,…,xn) составляется из наборов координат точек вершин единичного n-мерного куба.

(3) Аналитический способ задания

Приведем таблицы истинности, обозначения и названия булевых функций одного и двух аргументов. В табл. 1.4 представлены все (их 2^2^1=4) функции одного аргумента, в табл. 1.5 — все функции двух аргументов (их 2^2^2=16).

Таблица 1.4

x 0 1 Обозначение Название

0 0 0 0 Нуль, const 0

1 0 1 x Повторение x

2 1 0 ¬x, x Отрицание x, не x

3 1 1 1 Единица, const 1

Функции 0 и 1 называются соответственно тождественным нулем и тождественной единицей. Иногда эти функции 0 и 1 рассматривают как функции, зависящие от пустого множества переменных.

Таблица 1.5

x

у 0 0 1 1

0 1 0 1 Обозначение Название

0 0 0 0 0 0 Нуль, const 0

1 0 0 0 1 x•y,x∧y,x&y Конъюнкция

2 0 0 1 0 yx,x•y Запрет по x

3 0 0 1 1 x Повторение x

4 0 1 0 0 x, x•y Запрет по y

5 0 1 0 1 y Повторение y

6 0 1 1 0 x⊕y Сумма по модулю 2

7 0 1 1 1 x∨y Дизъюнкция

8 1 0 0 0 x↓y Стрелка Пирса

9 1 0 0 1 x~y Эквивалентность

10 1 0 1 0 ¬y, y Отрицание y

11 1 0 1 1 y→x, y⇒x, y⊃x Импликация от y к x

12 1 1 0 0 ¬x, x Отрицание x

13 1 1 0 1 x→y, x⇒y, x⊃y Импликация от x к y

14 1 1 1 0 x|y Штрих Шеффера

15 1 1 1 1 1 Единица, const 1

Функции одного и двух аргументов, представленные в таблицах 1.4 и 1.5, называются элементарными.

Символы ¬, |, ↓, ∧, , ∨, →, ⊕, ~, участвующие в обозначениях элементарных функций, называются логическими связками (операциями) или функциональными символами.

СДНФ

Поскольку между множеством аналитических представлений и множеством схем, реализующих булеву функцию, существует взаимнооднозначное соответствие, отыскание канонической форм представления булевой функции является начальным этапом синтеза схемы, ее реализующей. Наиболее широкое распространение получила совершенная дизъюнктивная нормальная форма (СДНФ). Прежде чем перейти к е¨ рассмотрению, приведем определение конституанты единицы: конституанта единицы - функция f(x1, x2, ... xn) принимающая значение 1 только на единственном наборе.

Конституанта единицы записывается как логическое произведение n различных булевых переменных, некоторые из них могут быть с отрицаниями. Ели вспомнить, что дизъюнкция равна 1, когда хотя бы одна из переменных принимает значение 1, то можно легко выразить любую булеву функцию как дизъюнкцию конституант единицы, соответствующих тем наборам, на которых функция равна 1.

Эта форма и есть СДНФ. Заметим, что наборы, на которых функция f принимает значение 1, часто называются единичными, остальные - нулевыми наборами. Выписывать в СДНФ имеет смысл только конституанты единицы, соответствующие единичным наборам.

Для функции T = {0, 1, 3, 4, 5, 7, 8, 9, 11, 12, 13, 15, 16, 17, 19, 20, 21, 23, 24, 25, 26, 27, 28, 29, 31}

СДНФ будет выглядеть следующим образом:

СКНФ

Другая известная форма носит название совершенной конъюнктивной нормальной формы (СКНФ). Она строится аналогично СДНФ.

Конституанта 0 – функция f(x1, x2, … xn) принимающая значение 0 только на единственном наборе.

Конституанта нуля записывается в виде элементарной дизъюнкции всех переменных. Каждому набору соответствует своя конституанта 0. СКНФ представляется как конъюнкция конституант нуля, соответствующих нулевым наборам функции.

Для функции T = {0, 1, 3, 4, 5, 7, 8, 9, 11, 12, 13, 15, 16, 17, 19, 20, 21, 23, 24, 25, 26, 27, 28, 29, 31}

СКНФ будет выглядеть следующим образом

3. Важнейшие аксиомы и теоремы алгебры логики. Реализация булевых функций в заданном базисе логических элементов. Учет ограничений на реализацию.

Преобразование формул ЛВ производят, как правило, для достижения следующих целей:

1) для получения более простого аналитического выражения, описывающего комбинационную схему (КС), вследствие чего синтезируемая КС также имеет меньшую конструктивную сложность;

2) для преобразования формулы ЛФ к регулярному виду, используемому для регуляризации и сравнения КС;

3) для получения СДНФ и СКНФ ЛВ.

В основе правил преобразований логических функций лежат законы, аксиомы и теоремы булевой алгебры.

Законы булевой алгебры

1 Закон коммутативности:                                

2 Закон ассоциативности:

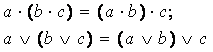
3 Закон дистрибутивности (распределительный закон):

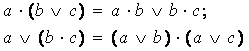
Аксиомы и теоремы булевой алгебры

1    , если   ;  , если   ;

2    ;  ;

3    ;  ;

4    ;  ;

5    ;  ;

6    ;  ;

7    ;  ;

8    ;  ;

9    ;  ;

10   ;  ;

11   ;