№1 История возникновения и развития натурального числа. Натур числа используемые для счета в практической деятельности появились на самых ранних этапах развития цивилизации. Термин «натуральное число» в первые употребил римский ученый и гос деятель А. Боэцкий (480-524). В XIXв внимание ученых было обращено на построение и логическое обоснование математических теорий натурального числа, те тех теорий, кот лежат в основе вычислений с натуральными с натуральными числами. Отвлеченное понятие натурального числа( те числа, не связанного с пересчетом конкретных предметов) появляется и закрепляется вместе с развитием письменности и введением для обозначения чисел определенных символов. После того как понятие натуральное число сформировалось, числа стали самостоятельными объектами и появилась возможность изучать их как математические объекты. Наука, кот стала изучать числа и действ над ними наз арифметикой. Расширение кажд числ множества историч было связ всегда 2мя факторами: 1практ деят-ть людей 2потребности самой математики.

№2Аксеометрический метод-способ построения научной теории, при котором в ее основу кладут аксиомы, из кот все ост утвержд этой теории(предметы законы св-ва) вводится чисто логическим путем, посредством докозательств. Аксиомы –высказывание некот теории принимаемое при дудуктивном построении этой теории без докозательства. Аксиоматическое построение множества целых неотрицательных чисел Z₀ . Множество Z₀ = N U {0}. 0 можно ввести изменив 1. И 4ю аксиомы Пеано следующим образом: 1) в множестве Z₀ существует элемент, непосредственно не следующий не за каким элементом этого множества. Называют его нулем и обозначают символом 0. 4) Пусть мно-во М есть подмножество множества Z₀ и известно что : а) 0 М б)из того что а€М, следует что а^,€М. Тогда множество М совпадает с мн Z₀ . Аксиома 2я и 3я остаются без изменения 2)для каждого элемента а из Z₀ существует единств элемент а^’ непосредственно следующий за а. 3)для каждого элемента из Z₀ существует не более 1го элемента, за кот не посредственно следует а. Cв-ва сложения и умножения целых неотриц чисел принимают вид: для сложения:1) ( ₀ ) [а+0=а] 2) ( ,b Z₀)[a+b^’=(a+b)’] для умножения 1) ( ₀ )[a*0=0], 2) ( ,b Z₀)[a*b’=a*b+a] определения операций вычитания и деления целых неотрицательных чисел аналогичны соответвующим определениям операций для натуральных чисел. При этом невозможно : значение 0:0 не определено, а частное а:0 при а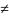 0 не существует. Все теоремы, доказанные для натуральных чисел, остаётся в силе для целых неотрицательных чисел.

№3 Математическая индукция- метод доказательства математических утверждений, основанный на принципе матем индукции, в основе которого лежит аксиома 4 Пеано. Доказательство методом математичесокй индукции утверждения А(n) состоит из двух частей: 1) базис индукции- доказывают, что утверждение А(n) истинно для n=1 т. е. доказывают истинность высказывания А(1). 2) индуктивный переход- предполагают что утверждение А(n) истинно для n=k и исходя из этого предположения доказывают что утверждение А(n) истинно и для n= k +1 то есть истинность высказывания А(k)=А(k+1). В этом случае К называют параметром индукции, А(k+1)- индуктивным предположением. Если А(1)^А(k)=> А(k+1)-тистинное высказывание, то делают вывод о том , что утверждение А(n)истинно для любого натурального числа т. математическая индукция широко используется при доказательстве неравенств, делимости чисел, нахождении суммы числовых последователей и т.п. доказательство методом математической индукции можно начинать не только с доказательства истинности утверждения А(n) считается доказанным для всех натуральных чисел n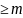 . Принцип математической индукции- если утверждение А(n) с натуральной переменной n истинно для n=1 и из того что оно истиннл для n=k (k- произвольное натуральное число) следует что оно истинно и для следующего числа n=k^’, то утверждение А(n) истинно для любого натурального числа т. Доказательство: Пусть М есть множество натуральных чисел, для которых верно данное утверждение. Тогда из условия теоремы имеем: а) 1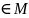 б) k => k^’ отсюда на основании четвертой аксиомы Пеано заключаем что М=N т. е. утверждение А(n) истинно для любого натурального числа n.

№4 сложение натуральных чисел алгебраическая операция,определенная на мно-ве N натуральных чисел и обладающая свойствами (аксиомами): 1)( [а+1=а^’] 2) )(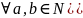 ^’] Число а+b называется суммой чисел а и b а сами числа слагаемыми. Пользуясь определением операции сложения можно составить таблицу сложения однозначных натуральных чисел. Таблицу составляют в следующей последовательности: сначала устанавливают как прибавлять к любому однозначному натуральному числу единицу, затем как прибавлять число два, потои –три , четыре и т.д. а) 1+1=1^’=2 ( на основании свойства 1-определения сложения) аналогично 2+1= 2^’=3? 3+1=3^’=4 и т.д. б)1+2=1+1^’=(1+1)^’=2^’=3^’( на основании свойства 2-определение сложения) , аналогично 2+2=2+1^’=(2+1)^’=3^’=4 и т.д. в) 1+3=1+2^’=(1+2)^’=3^’=4 ( на основании свойства 2-определения сложения) продолжая этот процесс получают всю таблицу сложения. Сложение натуральных чисел существует и единственно. Доказательство: докажем единственность. Если в множетсве N существует операция удовлетворяющая свойствам сложения 1 и 2, то она единственна. Предположим что во множестве N существуют две операции слодения, удовлетворяющие свойствам 1и 2. Обозначим одну из них знаком +, а другую знаком + в кружочке.Тогда для операции + имеем: 1) а+1=а^’ 2)а+b^’=(а+b)^’ а для операции + в кружочке соответственно: 1) а+в кружочке 1=а^’ 2) a+ в кружочке b^’=(a+ в кружочке b)^’ выберем некоторое число а и докажем что при этом а и любом b выполняется равенство: а+b=a+в кружочке b . Докозательство.проведем методом мат индукции. Справедливость равенства ( а+b= a+в кружочке b) при b=1 очевидна. Предположим, что равенство справедливо для некоторог произвольно выбранного натурального числа b. Исходя из предложения , докажем справедливость равенства (a+b=a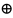 b) для числа b‘. В самом деле, по 2-му свойству, для операции «+» имеем: a+b’=(a b)’. 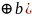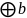По определению: (a+b’)=(a b)’; по второму св-ву для операции : (а ^’=a ^’ значит а+b^’=a b^’ на основании доказанного и принципа мат индукции заключаем, что равенство а+b=а b справедливо для любого числа b.так как при доказательстве число а выбрано произвольно, то равенство а+b=а b верно при любых натуральных числах а и b => операции + и на множестве N совпадают, и единственность сложения доказана. Докажем существование- в множетсве N существует операция удовлетворяющая свойствам сложения 1 и 2. Воспользуемся методом мат индукции. Докажем что при а=1 и любом в сложение можно производить по правилу: 1+b=b^’ пусть b=1 тогда по правилу => 1+1=1^’ , а это означает, что выполняется певое свойство сложения а+1=а^’ при а=1. Предположим что сложение по правилу удовлетворяет свойствам 1 и 2 для некоторого произвольно выбранного натурального числа b.

№5 коммуникативный закон сложения ( а+b=b+a] докозательство: проведем методом мат индукции . пусть b произвольно выбранное натуральное число. Покажем что 1+b =b+1 доказательство последнего равенства проведем индукцией по числу b. Пусть b=1 тогда равенство 1+1=1+1 очевидно. Предположим что равенство справедливо для некоторго произвольно выбранного числа b. Используя предположение докажем справедливость равенства для b^’ т.е. покажем что 1+b^’=b^’+1 по второму cв-ву сложения имеем 1+b^’=(1+b^’)= (b+1)^’=(b^’)^’ итак 1+b^’=(b^’)^’ а по первому свойству сложения b^’+1= ( b^’)^’ => 1+b^’= b^’+1 и справедливость равенства 1+b=b+1/ предположим что а+b=b+a для некоторго произвольно выбранного а. опираясь на предположение докажем справедливость равенства для а^’ т.е. покажем что а^’+b= b+a_’ по предположению а+b=b+a но тогда по второй аксиоме Пеано (а+b)^’=(b+a)^’ в свою очередь (а+b)^’=а^’+b, а (b+a)^’=b+a^’ по второму cв-ву операции сложения => а^’+b= b+a^’ . На основании доказанного и принципа мат индукции заключаем сто операция сложения натуральных чисел обладает свойством коммуникативности. Ассоциативный закон сложения (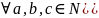 (а+b)+c=a+(b+c)] Доказательство: пусть а и b - натуральные числа , выбранные произвольно. Справедливость теолремы докажем методом мат индукции по переменной с. Проверим справедливость равенства при с=1 на основании свойств слродения имеем (а+b)+1=(a+b)^’=a+(b+1). Предположим что равенство справедливо для некоторог произвольно выбранного натурального числа с. Исходя из предположения докажем справедливость равенства для числа с^’ т.е. покажем что (а+b)+с^’=a+(b+c)^’. Повторому свойству операции сложения можем записать (а+b)+с^’=((а+b)+c)^’ . Попредположению((а+b)+c)^’ =(a+(b+c))^’. Далее по второму свойству операции слоджения (a+(b+c))^’=а+(b+c)^’=a+(b+c)^’. Итак (а+b)+с^’=а+(b+c^’) . все условия метода математической индукции выполнены и значит равенство справедливо для любого натурального числа с. А поскольку числа а и b были выбраны произвольно то ассоциативный закон сложения выполняется для любых натуральных чисел.

№6 умножение натуральных чисел- алгебраическая операция, определенная на множестве N натуральных чисел и обладающая свойствами( аксиомами): 1) ( [а*1=а] 2) )( ]. Число ab называется произведением чисел. Пользуясь определение опрации умножения можно составить таблицу умножении однозначных натуральных чисел. Таблицу составляют в следующей последовательности: сначала устанавливают как умножить любое однозначное натуральное число на единицу, затем как умножить число на два , потом на три, на четыре ит.д. а) 1*1=1 ( на основании свойства 1) определения умножения б) 1*2= 1*1^’+1=1+1=2( на основании свойства 2) определения умножения. в) 1*3=1*2+1=2+1=3 ( на основании свойства 2)определения сложения . Продолжая этот процесс получают всю таблицу умножения. Умножение натуральных чисел существует и оно единственно.

№7 1)коммуникативный закон умножения ( a*b=b*a] 2)Правый дистрибутивный закон умножения относительно сложения ( (b+c)a=ba+ca] 3)левый дистрибутивный закон умножения относительно сложения ( a(b+c)=ab+ac] 4)ассоциативный закон умножения ( (ab)c=a(bc)]

№8 разность натуральных чисел а и b – натуральное число с=а-b, удовлетворяющее условию b+c=а. Операция нахождения разности натуральных чисел а и b называется вычитанием из числа а числа b, число а называется уменьшаемым число b – вычитаемым. Таким образом вычитание это операция обратная сложению. Для любых натуральных чисел а b с справедливы следующие свойства: 1) правило вычитания числа из суммы. Чтобы вычесть число из суммы достаточно вычесть это число их одного из слагаемых суммы( если это возможно) и к полученному результату прибавить другое слагаемое т.е (a+b)-c={_{(b-c)+а ,если b больше с} ^{(a-c)+иб если а больше с} 2)правило вычитания суммы из числа. Чтобы вычесть из числа сумму чисел достаточно вычесть из этого числа последовательно каждое слагаемое одно за другим, т.е. а-(b+c)=(a+b)+с 3)правило вычитания числа из разности : (а-b)-c=a-(b+c)=a-b-c 4) правило вычитания разности из числа . Если а то а-(b-c)=(a-b)+с 5) правило прибавления разности к числу: а+(b-c)= (a+b)-c

№9 упорядочить множество N можно задав на нем отношение «меньше».Считают что число а меньше числа b тогда и только тогда когда существует такле натуральное число с, что а+с=b. В этом случае еще говорят что b больше а. Следствие 1. 1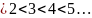 Следствие 2. Число 1- наименьшее число в N, то есть ( Отношение «меньше» на множестве N обладает следующими свойствами: 1) антирефлексивность- любое натуральное число не вступает в отношение «меньше» с самим собой, т.е. ( 2) ассиметричность – если а то неверно что b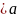 то есть ( а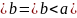 3) транзитивность- если а , b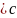 то а то есть( а . Введенное на множестве N бинарное отношение «меньше» в силу доказанного обладает свойствами ассиметричности, транзитивности и связанности , то есть является отношением строгого линейного порядка, а множество N- линейно упорядоченным множеством.

№10 1) теорема Архимеда- для любых натуральных чисел а и b существует натуральное число n, что nb . 2) принцип наименьшего числа- любое непустое подмножество натуральных чисел содержит наименьшее число. 3) принцип наибольшего числа- если М- непустое множество натуральных чисел и существует такое число b, что для любого числа х выполняется неравенство х , то в множестве М есть наибольшее число. 4) Свойство дискретности множества N – для любого а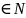 не существует натурального числа n такого что а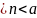 5) множество натуральных чисел N : а) бесконечное б) дискретное в) линейно упорядоченное г) счетное д) в нем имеется наименьшее число е) в нем выполняются принципы наименьшего и наибольшего числа и свойство Архимеда.

№11 частное натуральных чисел а b- натуральное число с=a*b, удовлетворяющие условию b*c=a. Операция нахождения частного натуральных чисел называется делением числа а на число b. Таким образом деление операция обратная умножению.Условия существования частного: для того чтобы существовало частное двух натуральных чисел а и b необходимо чтобы b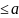 . Если частное существует то оно единственно. Эта теорема выражает необходимое условие существования частного двух натуральных чисел. Однако это условие не является достаточным. Так 25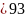 , но частное 93/25 не существует на множестве натуральных чисел.

№12 Число- одно из основных понятийматематики, возникшее впервые в связи с потребностями счета предметов. Построение системы целых неотрицательных чисел на основе теориимножества связано с именем Г.Кантора. В этой теории которую называют количественной теорией, основопологающим являются понятия конечного и взаимно однозначного соответствия. С теоретико- множественных позиций натуральное число рассматривается как число элементов конечного множества.Число 0 тоже имеет теоретико- множественное истолкование. Оно соответствует пустому множеству. Так как одному и тому же множеству соответствует только одно число, то вся совокупность конечных множеств распадается на классы равночисленных(эквивалентных) множеств. Поэтому натуральным числом называют общее свойство(инвариант) класса непустых эквивалентных множеств. Так число 5 – то общее свойство, которым обладают множества, содержащие пять пальцев, пять вершин пятиконечной звезды и т.п. Каждый класс определяется любым своим представлением. например отрезком натурального ряда.

№13 2 натуральных числа наз равными если соответсвующие им множества эквивалентны, в противном случае числа наз не равными, те если а=n(A), b=n(B) то а <=>b A~B a b  A~B. Отношение, равенства целых не отриц чисел обладает сл св-ми: 1)рефлексивность- любое цел неотриц число равно самому себе, те а=а 2) семметричность-если число а=числу b то и число b=a 3)транзитивность 2чила равные 3му равны между собой. Отношение равенства целых неотриц чисел явл отношением жквивалентности. Отношение «меньше» тоже имеет теоретико-множественное истолкование. Если мн-во А равномощно собственному подмножеству мн-ва B и n(A)=a n(B)=b говорят что число а меньше числа b в этой же ситуации говарят что b>a. Отношение «меньше» на множ целых неотриц чисел обладает сл св-ми:1)для люб отлич от 0 числа а справедливо неррав-во 0<a 2)антирефлексивность люб цел неотриц число не вступает в отношение «меньше»с самим собой те (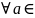 Z₀ )[(a<a)] 3)ассиметричность если a<b то не верно что b<a те ( Z₀ )[a<b=>b<a] 4) транзитивность- если a<b, b<c то a<c те (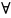 a,b,c Z₀ ) [a<b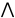 b<c=>a<c].

№14сложение целых неотриц чисел связано с операц объединения не пересекающихся конечных множеств. Сумма целых неотриц чисел а и b- число элементов в объеденении не пересекающихся множеств A и B таких, что n(A)=a n(B)=и те a+b=n(AUB), где a=n(A) b=n(B) A B= пустое множество. Для любых целых неотриц чисел аи b всегда существует единственное целое неотриц число с явл-ся их суммой ,те сумма любых 2х целых неотриц чисел сущ-ет и единственна. Определение суммы 2х целых неотриц чисел легко распростр на люб конеч число слогаемых. Действительно, при опред суммы 3х слогаемых а1,а2,а3 естественно поступить сл образом а1+а2+а3=(а1+а2)+а3 те сначало найти сумму 2х первых слогаемых и к получ результату прибывать 3е слогаемое. Предположем что определена сумма n слогаемых а1,а2…аn тогда сумма n+1 слогаемых нах-ся по правилу(а1+а2+…+аn+1)=(a1+a2+…+an)+an+1.

№15 законы и св-ва арифметических операций на мн-ве Z₀ практически полностью совпадают с аналогичными св-ми и законами арифметических операций на мн-ве N. Используя теоретика множественную трактовку докажем основные законы которым удоволетворяют арифм операции на множестве неотриц чисел. Для люб ЦНЧ a,b,c справедливы след законы арифм операций: 1)коммуникативность: a+b=b+a. Докозательство: построимтакие конеч множества A и B, что n(A)=a, n(B)=b и A непустое множ-во. Для люб множ-в справедлив каммуникативный закон объединения. Равные конечные мн-ва имеют равные численности те n(AUB)=n(BUA). По определению суммы ЦНЧ n(AUB)=n(A)+n(B)=a+b n(BUA)=n(B)+n(A)=b+a,=>a+b=b+a. верно для люб ЦНЧ.2) ассациативности (a+b)+c=a+(b+c). Камутативный и ассициативный законы сложения распростр-ся на люб конеч число слогаемых

№16вычитание ЦНЧa и b связ с выделением из мн-ва A(a=n(A)) подмножества B(b=n(B)). Разность ЦНЧ а и b- число элементов в дополнения мно-ва А при условии что n(A)=a, n(B)=b, B A, те a-b=n(AUB). Разность ЦНЧ a и b сущ-ет и единственна <=> b a, те ( Z₀ )(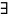 !c Z₀) [c=a-bb

№17 В количественной теории рассматривают различные подходы к определению произведения ЦНЧ. Так , взяв за основу понятие суммы, имеем след определение. Произведение ЦНЧ a и b- ЦНЧ a и b, кот удов сл условиям:1) ab=a+a+a+..+a(b раз) при b>1 2)a*1=a при b=1 3)a*0=0 при b=0 . Данное определение имеет сл теоретико-множ обоснование. Пустьданы в попарно непересекающихся мн-в А1,А2,…Аb, каждое из кот содержит а элементов. Тогда их объединение содержит a*b элементов. Существование и единственность произведения ЦНЧ при таком подходе вытекает из существования и единственности суммы. Для вывода законов умн-я, а так же законов связывающих умножение с другими операциями над ЦНЧ более удобен другой подход к определению произведения. Он связан с декартовым произведением мн-в. Произв ЦНЧ а и b – число элементов декартова произведения множ-в А и B, где n(A)=a, n(B)=иб те a*b=n(A*B), где а=n(A), b=n(B). Для любых ЦНЧ а и b всегда сущ-ет единственное ЦНЧ с, являющ их произведением, те произведение любых 2х ЦНЧ сущ-ет единственно.

№18 Используя теоретико-множественную трактовку докажем основные законы, которым удовлетворяют арифметичесике операции на множестве целых неотриц чисел. Для любых ЦНЧ а b и с справедливы след законы арифметических операций: 1) коммунитативности а* b=b*a 2) ассоциативности (а* b) *c=a(b*c) 3) дистрибутивности. Правый и левый дистрибутивные законы умножения относительно сложения: (а+ b)c=ac+bc ; с(а+b)=ca+cb Правый и левый дисрибут законы умножения относительно вычитания: (a-b)c=ac-bc c(a-b)=ca-cb. Докажем справедливость дистрибутивного закона умножения относительно сложения. Для этого построим конечные мн-ва A,B,C удоволетворяющ сл усл: n(A)=a n(B)=b n(С)=с и B C=Ø. Поскольку для люб мн-в имеет место дистрибутивность декартова произведения относительно объединения, то он выполняется и для построенных нами мн-в, те A*(BUC)=(A*B)U(A*C). Из равенства конечных множеств вытекает равенство их численностей. Это означает что n(A*(BUC))=n((A*B)U(A*C)). Но n(a*(BUC))=a(b*c) и n((A*B)U(A*C))=a*b+a*c и тд. Доказательство ост законов пров анологично. Заметим что коммутативный закон и ассоциативный умн-я справедливыдля люб конеч числа множитлей.

№19деление чисел связано с разбиением конечных мн-в равно численные попарно непересекющиеся подмнож-ва. При этом рещ-ся 2 задачи: нахождение числа элементов в каждом подмн-ве(деление на части) и нахождения числа таких подмножеств(деление по содержанию). Пусть а=n(A) и мн-во А разбито на папарно пересекающ равномощные подмнож-ва. Частным чисел а и b наз-число подмножеств в этом разбиении, если b- число элементов каждого подмножества в разбиении множ А; -число элементов в каждой подмножестве, если b-число подмножеств в разбиении множества. Если даны числа a и b, такие что a=n(A),b=n(B),a>b, и мн-во А можно разбить на n подмножеств, равномощных множеству В, то говорят , что число а больoше b в n раз, а число b меньше числа а в n раз. Невозможность деления на 0 также имеет свое теоретико- множественное истолкование. Если a 0, a b=0, то невозможность деления а на b вытекает из невозможности представления непустого конечного множества А(n(A)=a) в виде объединения пустых подмножеств.

№20система счисления- язык для наименования, записи чисел и выполнения действий над ними. Понятие системы счисления тесно связано с нумерацией- способ знаково- символического модулирования натуральных чисел. Различают: 1) устную номерацию- способ названия любого натурального числа с пом-ю определённых слов-имён числительных. 2) письменную нумерацию-способ обозначения любого натурального числа с пом-ю определённых знаков. Системы счисления делятся на: 1)позиционная система счисления, в котрой один и тот же знак может обозначать различные числа в зависимости от места (позиции) занимаемого этим знаком в записи числа. Позиционная система счисления характеризуется основанием (базисом)- количеством знаков или символов, используемых для изображения числа в разрядах данной системы счисления. Существует множество позиционных систем счисления . так как за основание системы счисления можно принять любое целое число р 2. Если р=2, то система наз-ся двоичной; если р=3 троичной и т.д. Основное достоинство позиционной системы счисления – простота выполнения арифметич опер-й , огр кол во символов необх для записи любых чисел. Позиц сист счисления- это система в кот каждый знак(и совакупности знаков принитой в донной системе для обозначения чисел) всегда обозначает одно и тоже число, независ от места занимаемого этим знаком записи числа. Одним из недостатков не позиц сист счисл явл в потребности введении новых знаков для записи больших чисел. Др не достатком явл ложность выполн арифм операций

Алгоритм умножения многозначного чнсла на

многозначное.

1. Записываем множитель х и под ним

2. второй множитель у.

3. Умножаем число х на цифру единиц

4. числа у и записываем результат

Под числом у.

З. Умножаем число х на цифру с

ледующего разряда числа у и

записы­ваем результат, сдвинув его

на один разряд влево относительно

пре­дыдущего результата.

4. Пункт 3 повторяем до тех пор. пока

5. будет найдено произведение числа х

6. на цифру старшего разряда у.

№21 десятичн запись натур числа S- представление числа S в виде S=a_n*10ⁿ+a_n-1*10^n-1+…+a1*10+a₀ где коэффициенты a_n и a_n-1…a₁ и а₀ принимают значение 0,1,2,3,4,5,6,7,8,9 и а_n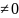 . Наибольшее распростронение получило 10-ная сист записи чисел напоминание о ней появл в 3 веке до н э а в совр мире она сложилась в 6 веке н э в индии. Сумму a_n*10ⁿ+a_n-1*10^n-1+…+a1*10+a₀ принято записывать в крат форме так : a_n* a_n-1…a₁a₀ черта с верху позволяет отличить эту запись от произв чисел a_n* a_n-1…a₁a₀ если в место букв пишутся цифры то черта не ставится. Числа изоображеные одной цифрой наз-ся однозначными 2мя цифрами 2значные, 3 цыфрами 3хзначные и тд . натур числа в кот все цифры кроме первой(слева) нули, наз-ся круглыми. Понятия числа и его запись не тождественны, поэтому сущ-е и единственность 10й записи натур числа нада доказать.

№22 ВЫПОЛНЕНИЕ АРИФМЕТИЧЕСКИХ ОПЕРАЦИЙ. Операции над чис­лами в позиционных системах счисления выполняются по определенным пра­вилам, которые принято называть алгоритмами. Надо лишь иметь соответству­ющие таблицы сложения и умножения однозначных чисел в р-ичной системе счисления. Таблица сложения играет большую роль в практике вычисления, т.к. сложение многозначных чисел сводится к поразрядному сложению однозначных чисел. Таблицу сложения однозначных чисел в десятичной системе (р = 10) со­ставляют и заучивают на память в начальной школе. На рис. 9.3 приведены табли­цы сложения и умножения для двоичной и для пятеричной систем счисления.

Замечание. В дальнейшем для удобства формулировок алгоритмов будем употреблять термин "цифра" вместо "однозначное число, изображаемое цифрой".

+	0		1
0	0		1
1	1		10
X		0		1
0		0		0
1		0		1

а) в двоичной системе счисления

+	0	1	2	3	4		X	0	1	2	3	4
0	0	1	2	3	4		Р	Q	0	Q	о	0
1	1	2	3	4	10		1	0	1	2	3	4
2	2	3	4	10	11		2	0	2	4	11	13 .
3	3	4	10	11	12		3	0	3	11	14	22
4	4	10	11	12	13		4	0	4	13	22	31

б) в пятеричной системе счисления , Рис. 9.3. Таблицы сложения и умножения однозначных чисел

В основе алгоритмов выполнения арифметических операций над многознач->1ми числами лежат следующие теоретические положения:

- способ записи чисел в десятичной системе счисления;

- коммутативный и ассоциативный законы сложения и умножения; правила вычитания числа из суммы и суммы из числа;

дистрибутивные законы умножения относительно сложения и вычитания; таблица сложения однозначных чисел.

Алгоритм сложения многозначных чисел.

I. Записываем второе слагаемое под первым так, чтобы соответствую­щие разряды находились друг под другом. 2 Складываем цифры первого разряда.

3. Если сумма меньше р, записываем ее в соответствующий разряд отве­та. Если сумма больше или равна р, то представляем ее в виде р + с, где с - однозначное число; записываем с в соответствующий разряд отве­та и прибавляем 1 к цифре следующего разряда первого слагаемого.

4 Переходим к следующему разряду. Складываем цифры этого разряда.

5 Пункты 3 и 4 повторяем до тех пор, пока будет найдена сумма цифр старших разрядов. При этом если сумма окажется больше или равна р, то приписываем впереди обоих слагаемых нули, увеличиваем нуль пе­ред первым слагаемым на 1 и выполняем сложение 1 +0 = 1.

Гак, в двоичной системе:

+ 1010111.

в пятеричной системе:

№ 23 Если цифра вычитаемого больше цифры уменьшаемого и цифры, стоящие в следующих старших разрядных уменьшаемого,равно 0, то берем первую отличную от нуля цифру в уменьшаемом(после те­кущего разряда), уменьшаем ее на 1, все цифры в младших разрядах увеличиваем на р - 1, а цифру в текущем разряде на р. Затем нахо­дим разность этого числа и соответствующей цифры вьiчитаемого, записав ее в соответствующий разряди искомого числа; 4) Переходим к следующему разряду. Вычитаем цифры этого разряда. 5) Пункты 3 И 4 повторяем до тех пор, пока не будет найдена разность цифр старших разрядов

№ 24 Алгоритм умножения многозначного числа ЩI однозначное.

1. Зрписываем второе число под первым.

2. Умножаем цифры разряда единиц числа х на число у.

3. Если произведение меньше р, его записываем в соответствующий разряд ответа.

Есть-произведение цифр соответствующего разряда-числа х на чис­ло у больше или равно р, то представляем его в виде pq + с, где с ­однозначное число; записываем с в соответствующий разряд ответа и запоминаем q.

4. Переходим к следующему разряду. Умножаем цифру этого разряда на число У, прибавляем к полученному произведению число q.

5. Пункты 3 и 4 повторяем до тех пор, пока будет найдено произведе­ние цифры старшего разряда числа х на число у.

Полученные произведения складываем

№25 Алгоритм деления многозначных чисел. Обобщением различных случа­ев деления целого неотрицательного числа х на натуральное число у является следующий алгоритм деления "уголком".

1Если х < у, то частное q = О, остаток r = х.

2Если х = у, то частное q = 1, остаток r = О.

З. Если х > У и число разрядов в числах х и у одинаково, То 'частное q находим перебором, последовательно умножая у на 1, 2, 3, ... , q - 1.

4. Если х > у и число разрядов в числе х больше, чем в числе у, то записываем делимое х и справа от него делитель У, который отделя­ем от х уголком. Выделяем в числе х столько старших разрядов, сколько разрядов в числе у или, если необходимо, на один разряд больше, но так, чтобы ОIIИ образовали число d,. большее или равное у. Перебором находим частное q, чисел d, и у, последовательно умно­жая у на 1, 2, З, .... , q, -1. Записываем q, под уголком (ниже у). Умно­жаем у на q, и записываем произведение под числом хтак, чтобы младший разряд числа yq, был написан под младшим разрядом вы­деленного числа d,. Проводим черту под yq, и находим разность г, = d, - yq,. Записываем под числоГ1 под числом yq,.

5. Приписываем справа к г, старший разряд из неиспользованных раз­рядов делимого Х и сравниваем полученное число (обозначим его d₂) с числом у.

6. Если d_2> у, то перебором находим частное % чисел d₂ и у, последо­вательно умножая у на 1, 2, З, ... , % :.. 1. Записываем q2 после q,. Умножаем у на % и записываем произведение под числом d₂ так, что­бы младший разряд числа yq2 был написан под младшим разрядом числа d₂. Проводим черту под yq2 и находим разность г, = d₂ - у%. Записываем разность г, под числом yq2' Переходим к пункту 5.

Если d₂ < у, то приписываем еще столько следующих разрядов (сколь­ко необходимо), чтобы получить число d2 большее или равное у. в этом случае записываем после q, такое же число нулей. Если при использовании младшего разряда числа х окажется, что d 2< у, то тогда частное чисел d2 и у равно нулю. Деление заканчиваем. Неполное

частное будет записано под уголком, остаток г =d2 В противном случае перебором находим частное q2 чисел d2 и у, последовательно умножая у на 1,2,3, ... , q2 -1. Частное % записываем после нулей. Умножаем у на q2 и записываем произведение под числом"х так, что­бы младший разряд числа eq2 был написан под младшим разрядом числа d2. Проводим черту под yq2 и находим разность г, = d2 - yq2' Записываем разность г, под числом yq2' Переходим к пункту 5.

Теорема 9.9 Число цифр частного двух натур-х чисел или равно разности между числом цифр делимого и числом цифр делителя или на еденицу больше этой разности.