Теорема Гюйгенса-Штейнера

Основная статья: Теорема Штейнера

Момент инерции твёрдого тела относительно какой-либо оси зависит не только от массы, формы и размеров тела, но также от положения тела по отношению к этой оси. Согласнотеореме Штейнера (теореме Гюйгенса-Штейнера), момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела J_c относительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела m на квадрат расстояния d между осями:

Если   — момент инерции тела относительно оси, проходящей через центр масс тела, то момент инерции относительно параллельной оси, расположенной на расстоянии   от неё, равен

,

где   — полная масса тела.

Например, момент инерции стержня относительно оси, проходящей через его конец, равен:

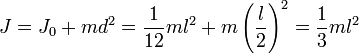
При вращении твердого тела относительно неподвижной оси каждый из его элементарных объемов массами m_i опишет окружность соответствующих радиусов r_i; при этом объем будет иметь соответствующую линейную скорость v_i. Но так как мы рассматриваем абсолютно твердое тело, то угловая скорость вращения этих объемов одинакова:   (1)  Кинетическую энергию вращающегося тела найдем как сумму кинетических энергий его элементарных объемов:   или    Используя выражение (1), получаем    где J_z - момент инерции тела относительно оси z. Таким образом, кинетическая энергия вращающегося тела   (2)  Из сравнения формулы (2) с выражением для кинетической энергии поступательно движущегося тела (T=mv²/2), мы видим, что момент инерции является мерой инертности тела при вращательном движении. Формула (2) справедлива для тела вращающегося вокруг неподвижной оси.  В качеcтве примера напишем формулу для плоского движения тела, например цилиндра, скатывающегося с наклонной плоскости без скольжения. Его энергия движения складывается из энергии поступательного движения и энергии вращения:    где m - масса катящегося тела; v_c - скорость центра масс тела; J_c - момент инерции тела относительно оси, проходящей через его центр масс; ω - угловая скорость тела.

Центр инерции и его движение. Определение

Положение центра масс (центра инерции) системы материальных точек в классической механике определяется следующим образом:

где

 — радиус-вектор центра масс,

 — радиус-вектор i-й точки системы,

 — масса i-й точки.

Для случая непрерывного распределения масс:

где:

 — суммарная масса системы,

 — объём,

 — плотность.

Центр масс, таким образом, характеризует распределение массы по телу или системе частиц.

[Править]Центры масс однородных фигур

• У отрезка — середина.

• У многоугольников (как сплошных плоских фигур, так и каркасов):

  • У параллелограмма — пересечение диагоналей.

  • У треугольника — точка пересечения медиан (центроид).

• У правильного многоугольника — центр поворотной симметрии.