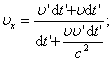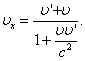- •Энтропия идеального газа. Адиабатический процесс как изоэнтропный. Изменение энтропии при изопроцессах с идеальным газом
- •Импульс, масса, кинетическая энергия в рел. Механике. Релятивистское выражение для импульса
- •Осевой момент инерции
- •Теорема Гюйгенса-Штейнера
- •Центр инерции и его движение. Определение
- •[Править]Центры масс однородных фигур
- •[Править]в механике
- •[Править]Центр масс в релятивистской механике
- •[Править]Вычисление момента
- •Кинетическая энергия. Кинетическая энергия
Распределение Больцмана.Пусть идеальный газ находится в поле консервативных сил в условиях теплового равновесия. При этом концентрация газа будет различной в точках с различной потенциальной энергией, что необходимо для соблюдения условий механического равновесия. Так, число молекул в единичном объеме n убывает с удалением от поверхности Земли, и давление, в силу соотношения P = nkT, падает. Если известно число молекул в единичном объеме, то известно и давление, и наоборот. Давление и плотность пропорциональны друг другу, поскольку температура в нашем случае постоянна. Давление с уменьшением высоты должно возрастать, потому что нижнему слою приходится выдерживать вес всех расположенных сверху атомов. Исходя из основного уравнения молекулярно-кинетической теории: P = nkT, заменим P и P0 в барометрической формуле на n и n0 и получим распределение Больцмана для молярной массы газа:
![]() где n0 и n -
число молекул в единичном объёме на
высоте h =
0 и h.
Так
как
где n0 и n -
число молекул в единичном объёме на
высоте h =
0 и h.
Так
как ![]() а
а ![]() ,
то можно представить в виде
,
то можно представить в виде
![]() (1.1).С
уменьшением температуры число молекул
на высотах, отличных от нуля, убывает.
При T =
0 тепловое движение прекращается, все
молекулы расположились бы на земной
поверхности. При высоких температурах,
наоборот, молекулы оказываются
распределёнными по высоте почти
равномерно, а плотность молекул медленно
убывает с высотой. Так как mgh–
это потенциальная энергия U,
то на разных высотах U
= mgh –
различна. Следовательно, (1.1) характеризует
распределение частиц по значениям
потенциальной энергии:
(1.1).С
уменьшением температуры число молекул
на высотах, отличных от нуля, убывает.
При T =
0 тепловое движение прекращается, все
молекулы расположились бы на земной
поверхности. При высоких температурах,
наоборот, молекулы оказываются
распределёнными по высоте почти
равномерно, а плотность молекул медленно
убывает с высотой. Так как mgh–
это потенциальная энергия U,
то на разных высотах U
= mgh –
различна. Следовательно, (1.1) характеризует
распределение частиц по значениям
потенциальной энергии:
![]() – это
закон распределения частиц по
потенциальным энергиям – распределение
Больцмана. Здесь n0 –
число молекул в единице объёма там,
где U =
0. можно
получить, что отношение концентраций
молекул в точках с U1 и
i>U2 равно:
– это
закон распределения частиц по
потенциальным энергиям – распределение
Больцмана. Здесь n0 –
число молекул в единице объёма там,
где U =
0. можно
получить, что отношение концентраций
молекул в точках с U1 и
i>U2 равно:
![]() .
.
Распределение
Максвелла.
Молекулы газа вследствие теплового
движения испытывают многочисленные
соударения друг с другом. При каждом
соударении скорости молекул изменяются
как по величине, так и по направлению.
В результате в сосуде, содержащем
большое число молекул, устанавливается
некоторое статистическое распределение
молекул по скоростям, зависящее от
абсолютной температуры Т. При этом все
направления векторов скоростей молекул
оказываются равноправными (равновероятными),
а величины скоростей подчиняются
определенной закономерности. Распределение
молекул газа по величине скоростей
называется распределением Максвелла.Если
одновременно измерить скорости большого
числа N молекул газа и выделить некоторый
малый интервал скоростей от v до v+![]() v,
то в выделенный интервал
v
попадает некоторое число
N
молекул. На графике удобно изображать
зависимость величины
v,
то в выделенный интервал
v
попадает некоторое число
N
молекул. На графике удобно изображать
зависимость величины ![]() от скорости v. При достаточно большом
числе N эта зависимость изображается
плавной кривой, имеющей максимум
при
от скорости v. При достаточно большом
числе N эта зависимость изображается
плавной кривой, имеющей максимум
при ![]() (наиболее
вероятная скорость). Здесь m - масса
молекулы,
(наиболее
вероятная скорость). Здесь m - масса
молекулы, ![]() -
постоянная Больцмана.Характерным
параметром распределения Максвелла
является так называемая среднеквадратичная
скорость
-
постоянная Больцмана.Характерным
параметром распределения Максвелла
является так называемая среднеквадратичная
скорость ![]() означает
среднее значение квадрата скорости. В
молекулярной физике доказывается, что
означает
среднее значение квадрата скорости. В
молекулярной физике доказывается, что
![]() ,где
,где ![]() -
молярная масса.Из выражения для
среднеквадратичной скорости следует,
что средняя кинетическая энергия
поступательного движения молекул газа
есть
-
молярная масса.Из выражения для
среднеквадратичной скорости следует,
что средняя кинетическая энергия
поступательного движения молекул газа
есть![]()
Необратимые
процессы. Принцип возрастания энтропии.
Примеры.
Понятие
энтропии впервые введено в 1865 г. Р.
Клаузиусом. Для определения физического
содержания этого понятия берут отношение
теплоты Q, которое получило тело в
изотермическом процессе, к температуре
Т теплоотдающего тела, называемое приведенным
количеством теплоты. Приведенное
количество теплоты, которое сообщается
телу на малом участке процесса, равно
δQ/T. Строгий формальный анализ показывает,
что приведенное количество теплоты,
которое сообщается телу в любом обратимом
круговом процессе, равно нулю: ![]() (1) Из
равенства нулю интеграла (1), взятого
по замкнутому контуру, следует, что
подынтегральное выражение δQ/T есть
полный дифференциал некоторой функции,
которая определяется только состоянием
системы и не зависит от пути, которым
система пришла в это состояние. Таким
образом,
(1) Из
равенства нулю интеграла (1), взятого
по замкнутому контуру, следует, что
подынтегральное выражение δQ/T есть
полный дифференциал некоторой функции,
которая определяется только состоянием
системы и не зависит от пути, которым
система пришла в это состояние. Таким
образом,
![]() (2) Функция
состояния, у которой дифференциал равен
δQ/T, называется энтропией и
обозначается S. Из
формулы (1) следует, что для обратимых
процессов изменение энтропии
(2) Функция
состояния, у которой дифференциал равен
δQ/T, называется энтропией и
обозначается S. Из
формулы (1) следует, что для обратимых
процессов изменение энтропии ![]() (3)
В
термодинамике доказывается, что энтропия
системы, совершающей необратимый цикл,
возрастает:
(3)
В
термодинамике доказывается, что энтропия
системы, совершающей необратимый цикл,
возрастает: ![]() (4) Выражения
(3) и (4) применяются только к замкнутым
системам, если же система обменивается
теплотой с внешней средой, то ее энтропия
может вести себя произвольным образом.
Соотношения (3) и (4) можно представить
в виде неравенства
Клаузиуса
(4) Выражения
(3) и (4) применяются только к замкнутым
системам, если же система обменивается
теплотой с внешней средой, то ее энтропия
может вести себя произвольным образом.
Соотношения (3) и (4) можно представить
в виде неравенства
Клаузиуса
![]() (5) т.
е. энтропия
замкнутой системы может либо возрастать (в
случае необратимых процессов), либо
оставаться постоянной (в
случае обратимых процессов). Если
система совершает равновесный переход
из состояния 1 в состояние 2, то, согласно
(2), изменение энтропии
(5) т.
е. энтропия
замкнутой системы может либо возрастать (в
случае необратимых процессов), либо
оставаться постоянной (в
случае обратимых процессов). Если
система совершает равновесный переход
из состояния 1 в состояние 2, то, согласно
(2), изменение энтропии
![]() (6) где
подынтегральное выражение и пределы
интегрирования определяются через
величины, которые характеризуют
рассматриваемый процесс. Формула (6)
определяет энтропию лишь с точностью
до аддитивной постоянной (слагаемого).
Физический смысл имеет не сама энтропия,
а разность энтропий.
Используя
выражение (6), найдем изменение энтропии
в процессах идеального газа. Taк как
dU=(m/M)CVdT,
δA=pdV=(m/M)RT(dV/V) , то
(6) где
подынтегральное выражение и пределы
интегрирования определяются через
величины, которые характеризуют
рассматриваемый процесс. Формула (6)
определяет энтропию лишь с точностью
до аддитивной постоянной (слагаемого).
Физический смысл имеет не сама энтропия,
а разность энтропий.
Используя
выражение (6), найдем изменение энтропии
в процессах идеального газа. Taк как
dU=(m/M)CVdT,
δA=pdV=(m/M)RT(dV/V) , то
![]() или
или ![]() (7)
т.
е. изменение энтропии ΔS1→2 идеального
газа при переходе его из cоcтояния 1 в
cоcтояние 2 не
завиcит от вида процеccа перехода
1→2. Так
как для адиабатического процесса δQ =
0, то ΔS = 0 и, следовательно, S=const, т.
е. адиабатический
обратимый процесс протекает при
постоянной энтропии.
Поэтому его часто называют изоэнтропийным
процессом.
Из формулы (7) следует, что при изотермическом
процессе (T1=
T2)
(7)
т.
е. изменение энтропии ΔS1→2 идеального
газа при переходе его из cоcтояния 1 в
cоcтояние 2 не
завиcит от вида процеccа перехода
1→2. Так
как для адиабатического процесса δQ =
0, то ΔS = 0 и, следовательно, S=const, т.
е. адиабатический
обратимый процесс протекает при
постоянной энтропии.
Поэтому его часто называют изоэнтропийным
процессом.
Из формулы (7) следует, что при изотермическом
процессе (T1=
T2)
![]() при
изохорном процессе (V1 =
V2)
при
изохорном процессе (V1 =
V2)
![]() Энтропия
обладает свойством аддитивности:
энтропия системы равна сумме энтропий
тел, которые входят в систему. Свойством
аддитивности обладают также внутренняя
энергия, масса, объем (но таким свойством
не обладают температура и давление). Более
глубокий смысл энтропии показывается
в статистической физике: энтропия
связывается с термодинамической
вероятностью состояния
системы. Термодинамическая
вероятность W
состояния системы — это число способов,
с помощью которых может быть реализовано
данное состояние макроскопической
системы, или число микросостояний,
которые осуществляют данное макросостояние
(по определению, W≥1, т. е. термодинамическая
вероятность не есть вероятность в
математическом смысле (последняя ≥1
!!!)). Cогласно
Больцману, энтропия cиcтемы и
термодинамическая вероятность связаны
между собой следующим образом:
Энтропия
обладает свойством аддитивности:
энтропия системы равна сумме энтропий
тел, которые входят в систему. Свойством
аддитивности обладают также внутренняя
энергия, масса, объем (но таким свойством
не обладают температура и давление). Более
глубокий смысл энтропии показывается
в статистической физике: энтропия
связывается с термодинамической
вероятностью состояния
системы. Термодинамическая
вероятность W
состояния системы — это число способов,
с помощью которых может быть реализовано
данное состояние макроскопической
системы, или число микросостояний,
которые осуществляют данное макросостояние
(по определению, W≥1, т. е. термодинамическая
вероятность не есть вероятность в
математическом смысле (последняя ≥1
!!!)). Cогласно
Больцману, энтропия cиcтемы и
термодинамическая вероятность связаны
между собой следующим образом: ![]() (8) где
k — постоянная Больцмана. Таким образом,
энтропия определяется логарифмом числа
микросостояний, с помощью которых может
быть осуществлено данное макросостояние.
Значит, энтропия может рассматриваться
как мера вероятности состояния
термодинамической системы. Формула
Больцмана (8) позволяет дать энтропии
следующее статистическое толкование: энтропия
является мерой неупорядоченности
системы.
Действительно, чем больше число
микросостояний, которые реализуют
данное макросостояние, тем больше
энтропия. В состоянии равновесия —
наиболее вероятного состояния системы
— число микросостояний максимально,
при этом также максимальна и энтропия. Так
как реальные процессы необратимы, то
можно говорить, что все процессы в
замкнутой системе ведут к увеличению
ее энтропии —принцип
возрастания энтропии.
При статистическом толковании энтропии
это означает, что процессы в замкнутой
системе идут в направлении увеличения
числа микросостояний, другими словами,
от менее вероятных состояний к более
вероятным, до тех пор пока вероятность
состояния не станет максимальной.
(8) где
k — постоянная Больцмана. Таким образом,
энтропия определяется логарифмом числа
микросостояний, с помощью которых может
быть осуществлено данное макросостояние.
Значит, энтропия может рассматриваться
как мера вероятности состояния
термодинамической системы. Формула
Больцмана (8) позволяет дать энтропии
следующее статистическое толкование: энтропия
является мерой неупорядоченности
системы.
Действительно, чем больше число
микросостояний, которые реализуют
данное макросостояние, тем больше
энтропия. В состоянии равновесия —
наиболее вероятного состояния системы
— число микросостояний максимально,
при этом также максимальна и энтропия. Так
как реальные процессы необратимы, то
можно говорить, что все процессы в
замкнутой системе ведут к увеличению
ее энтропии —принцип
возрастания энтропии.
При статистическом толковании энтропии
это означает, что процессы в замкнутой
системе идут в направлении увеличения
числа микросостояний, другими словами,
от менее вероятных состояний к более
вероятным, до тех пор пока вероятность
состояния не станет максимальной.
Второй Закон Термодинамики, как и Первый (Закон сохранения энергии) установлен эмпирическим путем. Впервые его сформулировал Клаузиус: "теплота сама собой переходит лишь от тела с большей температурой к телу с меньшей температурой и не может самопроизвольно переходить в обратном направлении".Другая формулировка: все самопроизвольные процессы в природе идут с увеличением энтропии. (Энтропия - мера хаотичности, неупорядоченности системы).Рассмотрим систему из двух контактирующих тел с разными температурами. Тепло пойдет от тела с большей температурой к телу с меньшей, до тех пор, пока температуры обоих тел не выровняются. При этом от одного тела к другому будет передано определенное количество тепла dQ. Но энтропия при этом у первого тела уменьшится на меньшую величину, чем она увеличится у второго тела, которое принимает теплоту, так как, по-определению, dS=dQ/T (температура в знаменателе!). То есть, в результате этого самопроизвольного процесса энтропиясистемы из двух тел станет больше суммы энтропий этих тел до начала процесса. Иначе говоря, самопроизвольный процесс передачи тепла от тела с высокой Т к телу с более низкой Т привел к тому, что энтропия системы из этих двух тел увеличилась!Заметим, что, рассматривая эту систему из двух тел, мы подразумевали, что внешнего теплопритока в нее или теплооттока из нее нет (для простоты, чтобы не пудрить себе мозги) - то есть, считали ее изолированной (или замкнутой). Отсюда еще одна формулировка Второго Закона Термодинамики: "При прохождении в изолированной системе самопроизвольных процессов энтропия системы возрастает". Или: "Энтропия изолированной системы стремится к максимуму" - так как самопроизвольные процессы передачи тепла всегда будут происходить, пока есть перепады температур.А что будет, если наша система из двух тел будет неизолирована (незамкнута) и, допустим, в нее поступает тепло? Ясно, что ее энтропия будет увеличиваться еще больше, так как при получении телом тепла энтропия его увеличивается (dS=dQ/T).Но для простоты формулировки этот момент обычно не упоминают и поэтому формулируют Второй Закон термодинамики именно для изолированных систем. Хотя, как мы видим, он действует точно также и для открытых систем в случае поступления в них тепла. И представьте, эти идиоты эволюционисты уперлись в общепринятую формулировку Второго Закона термодинамики для изолированных систем, утверждая, что, мол, если система открыта, то Второй Закон Термодинамики не действует! Это какими же тупыми и безмозглыми надо быть, что даже мозгами чуть-чуть лень пошевелить, чтобы понять такую простую истину, что дляоткрытой системы с подведением тепла энтропия растет даже быстрее, чем для изолированной!
Циклы
и тепловые машины. Цикл Карно и его КПД.
Оптимальность цикла Карно.
Цикл Карно́ — идеальный термодинамический
цикл. Тепловая машина Карно, работающая
по этому циклу, обладает максимальным
КПД из всех машин, у которых максимальная
и минимальная температуры осуществляемого
цикла совпадают соответственно с
максимальной и минимальной температурами
цикла Карно. Состоит из 2 адиабатических
и 2 изотермических процессов.
Описание цикла Карно
 Цикл
Карно в координатах P и V
Цикл
Карно в координатах P и V
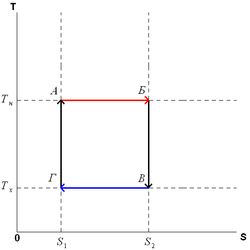 Цикл
Карно в координатах T и S. Пусть тепловая
машина состоит
из нагревателя с температурой
Цикл
Карно в координатах T и S. Пусть тепловая
машина состоит
из нагревателя с температурой ![]() ,
холодильника с температурой
,
холодильника с температурой ![]() и рабочего
тела.
Цикл Карно состоит из четырёх
стадий:Изотермическое
расширение (на
рисунке — процесс A→Б). В начале
процесса рабочее тело имеет температуру
,
то есть температуру нагревателя. Затем
тело приводится в контакт с нагревателем,
который изотермически (при постоянной
температуре) передаёт ему количество
теплоты
и рабочего
тела.
Цикл Карно состоит из четырёх
стадий:Изотермическое
расширение (на
рисунке — процесс A→Б). В начале
процесса рабочее тело имеет температуру
,
то есть температуру нагревателя. Затем
тело приводится в контакт с нагревателем,
который изотермически (при постоянной
температуре) передаёт ему количество
теплоты ![]() .
При этом объём рабочего тела
увеличивается.Адиабатическое
(изоэнтропическое) расширение (на
рисунке — процесс Б→В). Рабочее тело
отсоединяется от нагревателя и продолжает
расширяться без теплообмена с окружающей
средой. При этом его температура
уменьшается до температуры
холодильника.Изотермическое
сжатие (на
рисунке — процесс В→Г). Рабочее
тело, имеющее к тому времени температуру
,
приводится в контакт с холодильником
и начинает изотермически сжиматься,
отдавая холодильнику количество
теплоты
.
При этом объём рабочего тела
увеличивается.Адиабатическое
(изоэнтропическое) расширение (на
рисунке — процесс Б→В). Рабочее тело
отсоединяется от нагревателя и продолжает
расширяться без теплообмена с окружающей
средой. При этом его температура
уменьшается до температуры
холодильника.Изотермическое
сжатие (на
рисунке — процесс В→Г). Рабочее
тело, имеющее к тому времени температуру
,
приводится в контакт с холодильником
и начинает изотермически сжиматься,
отдавая холодильнику количество
теплоты ![]() .
Адиабатическое
(изоэнтропическое) сжатие (на
рисунке — процесс Г→А). Рабочее тело
отсоединяется от холодильника и
сжимается без теплообмена с окружающей
средой. При этом его температура
увеличивается до температуры
нагревателя.При изотермических процессах
температура остаётся постоянной, при
адиабатических отсутствует теплообмен,
а значит, сохраняется энтропия:
.
Адиабатическое
(изоэнтропическое) сжатие (на
рисунке — процесс Г→А). Рабочее тело
отсоединяется от холодильника и
сжимается без теплообмена с окружающей
средой. При этом его температура
увеличивается до температуры
нагревателя.При изотермических процессах
температура остаётся постоянной, при
адиабатических отсутствует теплообмен,
а значит, сохраняется энтропия:
![]() при
при ![]() .Поэтому
цикл Карно удобно представить в
координатах T и S (температура и энтропия).
.Поэтому
цикл Карно удобно представить в
координатах T и S (температура и энтропия).
Энтропия идеального газа. Адиабатический процесс как изоэнтропный. Изменение энтропии при изопроцессах с идеальным газом
Изоэнтропные
процессы — это обратимые адиабатические
процессы, ным примером такого процесса
является горение топлива в камере
сгорания ракетного двигателя с его
последующим истечением через сопло.
Энтропия системы является функцией ее
состояния, определенная с точностью
до произвольной постоянной. Процесс
горения и расширения газа можно считать
адиабатическим, так скорость тепловыделения
гораздо больше скорости и обратимым
ввиду совершения системой реактивной
работы, близкой к максимальной.
. Согласно второму
началу термодинамики,
при обратимом адиабатическом
процессе энтропия постоянна, ![]() ,
а при необратимом – возрастает.
Обратимый адиабатический процесс,
называется также изоэнтропийным,
изображается на диаграмме
состояния адиабатой (изоэнтропой).
Если система совершает равновесный
переход из состояния 1 в состояние 2, то
изменение энтропии
,
а при необратимом – возрастает.
Обратимый адиабатический процесс,
называется также изоэнтропийным,
изображается на диаграмме
состояния адиабатой (изоэнтропой).
Если система совершает равновесный
переход из состояния 1 в состояние 2, то
изменение энтропии
|
|
|
(6.2.1) |
Таким образом, по формуле (6.2.1) можно определить энтропию лишь с точностью до аддитивной постоянной, т.е. начало энтропии произвольно. Физический смысл имеет лишьразность энтропий. Исходя из этого, найдем изменения энтропии в процессах идеального газа. Так как при Т = const,
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(6.2.2) |
Таким образом, изменение энтропии ΔS1-2 идеального газа при переходе его из состояния 1 в состояние 2 не зависит от вида перехода 1 - 2. Каждый из изопроцессов идеального газа характеризуется своим изменением энтропии, а именно:
изохорический:
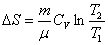 ,
т.к.
,
т.к. 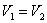 ;
;изобарический:
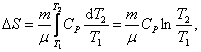 т.к. Р1 =
Р2;
т.к. Р1 =
Р2;изотермический:
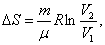 т.к.
т.к. 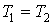 ;
;адиабатический:
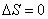 ,
т.к.
,
т.к. 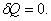
Отметим,
что в последнем случае адиабатический
процесс называют изоэнтропийным
процессом,
т.к. ![]() .
.
 Энтропия.
Примеры.
Энтропия – это одна из функций состояния
термодинамической системы. Функция
состояния – это такая величина, значения
которой однозначно определяются
состоянием системы, а изменение функции
состояния при переходе системы из
одного состояния в другое определяется
только начальным и конечным состояниями
системы и не зависят от пути
перехода.Например, внутренняя энергия
U
– функция
состояния. Внутренняя энергия идеального
газа равна
Энтропия.
Примеры.
Энтропия – это одна из функций состояния
термодинамической системы. Функция
состояния – это такая величина, значения
которой однозначно определяются
состоянием системы, а изменение функции
состояния при переходе системы из
одного состояния в другое определяется
только начальным и конечным состояниями
системы и не зависят от пути
перехода.Например, внутренняя энергия
U
– функция
состояния. Внутренняя энергия идеального
газа равна
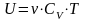 ,
и её изменение определяется только
начальной и конечной температурами:
,
и её изменение определяется только
начальной и конечной температурами:
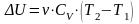 .
Величина
.
Величина
 – это молярная теплоёмкость идеального
газа при постоянном объёме. Количество
теплоты Q
и работа A
не являются функциями состояния: они
зависят от пути перехода системы из
начального состояния в конечное.
Например, пусть идеальный газ переходит
из состояния 1 в состояние 2, совершив
последовательно сначала изобарный
процесс, затем – изохорный (рис.1, а).
Тогда совершённая за весь процесс
работа равна
– это молярная теплоёмкость идеального
газа при постоянном объёме. Количество
теплоты Q
и работа A
не являются функциями состояния: они
зависят от пути перехода системы из
начального состояния в конечное.
Например, пусть идеальный газ переходит
из состояния 1 в состояние 2, совершив
последовательно сначала изобарный
процесс, затем – изохорный (рис.1, а).
Тогда совершённая за весь процесс
работа равна
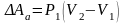 .
Пусть теперь из 1 в 2 идеальный газ
переходит, сначала совершив изохорный
процесс, а затем изобарный (рис.1, b).
Работа при таком переходе равна
.
Пусть теперь из 1 в 2 идеальный газ
переходит, сначала совершив изохорный
процесс, а затем изобарный (рис.1, b).
Работа при таком переходе равна
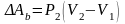 .
Очевидно,
.
Очевидно,
 .
Величина работы оказалась разная, хотя
начальное и конечное состояние одинаковы.
Поскольку по первому закону термодинамики
количество теплоты, сообщённое системе,
идёт на приращение внутренней энергии
и на работу системы против внешних сил:
.
Величина работы оказалась разная, хотя
начальное и конечное состояние одинаковы.
Поскольку по первому закону термодинамики
количество теплоты, сообщённое системе,
идёт на приращение внутренней энергии
и на работу системы против внешних сил:
 ,
то теплота, полученная системой в
процессах a
и
b,
тоже будет разной, то есть теплота также
не является функцией состояния.
,
то теплота, полученная системой в
процессах a
и
b,
тоже будет разной, то есть теплота также
не является функцией состояния.
С точки зрения
математики, малые приращения величин,
не являющихся функциями состояния, не
будут полными дифференциалами, и для
них нужно использовать обозначения: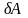 и
и
 .
Оказывается, что для теплоты интегрирующим
множителем является обратная температура:
.
Оказывается, что для теплоты интегрирующим
множителем является обратная температура:
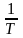 ,
и величина, равная отношению полученной
системой теплоты к абсолютной температуре,
является полным дифференциалом – это
приведённая теплота:
,
и величина, равная отношению полученной
системой теплоты к абсолютной температуре,
является полным дифференциалом – это
приведённая теплота:
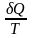 .
По определению Клаузиуса, функция
состояния системы, дифференциал которой
равен приведённой теплоте, является
энтропией:
.
По определению Клаузиуса, функция
состояния системы, дифференциал которой
равен приведённой теплоте, является
энтропией:
 .
(1) Свойства
энтропии:
1) Энтропия – функция состояния системы,
то есть в замкнутой системе в обратимом
процессе, когда система возвращается
в исходное состояние, полное изменения
энтропии равно нулю:
.
(1) Свойства
энтропии:
1) Энтропия – функция состояния системы,
то есть в замкнутой системе в обратимом
процессе, когда система возвращается
в исходное состояние, полное изменения
энтропии равно нулю: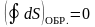 .
(2). 2) Энтропия аддитивна, то есть энтропия
системы равна сумме энтропий всех её
частей. 3) Энтропия замкнутой системы
не убывает:
.
(2). 2) Энтропия аддитивна, то есть энтропия
системы равна сумме энтропий всех её
частей. 3) Энтропия замкнутой системы
не убывает:
 ,
(3). причём
,
(3). причём
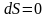 для обратимых процессов и
для обратимых процессов и
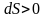 для необратимых. Соотношение (3) называется
неравенством
Клаузиуса
и представляет собой одну из формулировок
второго
начала термодинамики:
энтропия
замкнутой системы остаётся постоянной,
если в ней происходят только обратимые
процессы, и возрастает в случае
необратимых процессов.
Рассмотрим замкнутую систему, состоящую
из двух тел с температурами
для необратимых. Соотношение (3) называется
неравенством
Клаузиуса
и представляет собой одну из формулировок
второго
начала термодинамики:
энтропия
замкнутой системы остаётся постоянной,
если в ней происходят только обратимые
процессы, и возрастает в случае
необратимых процессов.
Рассмотрим замкнутую систему, состоящую
из двух тел с температурами
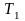 и
и
 .
Пусть
– количество теплоты, полученное вторым
телом от первого
.
Пусть
– количество теплоты, полученное вторым
телом от первого
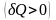 .
Тогда количество теплоты, полученное
первым телом, отрицательно и равно
.
Тогда количество теплоты, полученное
первым телом, отрицательно и равно
 .
Полное приращение энтропии системы
двух тел в процессе теплопередачи равно
сумме изменений энтропий двух тел:
.
Полное приращение энтропии системы
двух тел в процессе теплопередачи равно
сумме изменений энтропий двух тел:
 .
(4) Процесс теплопередачи может быть
обратим лишь в случае, если температуры
тел равны:
.
(4) Процесс теплопередачи может быть
обратим лишь в случае, если температуры
тел равны:
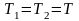 .
При неравенстве температур обратный
процесс невозможен: теплота
сама собой от холодного к нагретому
идти не может
– это ещё одна формулировка второго
начала термодинамики. Тогда из (4)
получим:
.
При неравенстве температур обратный
процесс невозможен: теплота
сама собой от холодного к нагретому
идти не может
– это ещё одна формулировка второго
начала термодинамики. Тогда из (4)
получим:
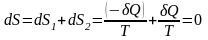 .
(5) Процесс передачи теплоты от первого
тела ко второму будет необратимым, если
.
(5) Процесс передачи теплоты от первого
тела ко второму будет необратимым, если
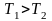 .
Тогда
.
Тогда
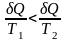 ,
и из (4)
,
и из (4)
 .
(6)
.
(6)
Адиабатический
процесс. Уравнение адиабаты.
Адиабатический
процесс (адиабатный
процесс)
- термодинамический
процесс,
происходящий в системе без теплообмена
с окружающей средой (![]() ),
т. е. в адиабатически изолированной
системе, состояние которой можно
изменить только путем изменения внешних
параметров. Понятиеадиабатической
изоляции является
идеализацией теплоизолирующих оболочек
или сосудов Дьюара (адиабатные оболочки).
Изменение температуры внешних тел не
оказывает влияния на адиабатически
изолированной системы, а их энергия U может
изменяться только за счет работы,
совершаемой системой (или над ней).
Согласно первому
началу термодинамики,
при обратимом адиабатическом процессе
для однородной
системы
),
т. е. в адиабатически изолированной
системе, состояние которой можно
изменить только путем изменения внешних
параметров. Понятиеадиабатической
изоляции является
идеализацией теплоизолирующих оболочек
или сосудов Дьюара (адиабатные оболочки).
Изменение температуры внешних тел не
оказывает влияния на адиабатически
изолированной системы, а их энергия U может
изменяться только за счет работы,
совершаемой системой (или над ней).
Согласно первому
началу термодинамики,
при обратимом адиабатическом процессе
для однородной
системы ![]() ,
где V - объем системы, p - давление,
а в общем случае
,
где V - объем системы, p - давление,
а в общем случае ![]() ,
где aj,
- внешние параметры, Аj - термодинамические
силы.
Согласно второму
началу термодинамики,
при обратимом адиабатическом
процессе энтропия постоянна,
,
а при необратимом - возрастает. Очень
быстрые процессы, при которых не успевает
произойти теплообмен с
окружающей средой, например,
прираспространении
звука,
можно рассматривать как адиабатический
процесс. Энтропия каждого малого
элемента жидкости при его движении со
скоростью v остается
постоянной, поэтому полная производная
энтропии s,
отнесенной к единице массы, равна
нулю,
,
где aj,
- внешние параметры, Аj - термодинамические
силы.
Согласно второму
началу термодинамики,
при обратимом адиабатическом
процессе энтропия постоянна,
,
а при необратимом - возрастает. Очень
быстрые процессы, при которых не успевает
произойти теплообмен с
окружающей средой, например,
прираспространении
звука,
можно рассматривать как адиабатический
процесс. Энтропия каждого малого
элемента жидкости при его движении со
скоростью v остается
постоянной, поэтому полная производная
энтропии s,
отнесенной к единице массы, равна
нулю, ![]() (условие
адиабатичности).
Простым примером адиабатического
процесса является сжатие (или расширение)
газа в теплоизолированном цилиндре с
теплоизолированным поршнем: при сжатии
температуpa возрастает, при расширении
- убывает. Другим примером адиабатического
процесса может служить адиабатическое
размагничивание, которое используют
в методе магнитного охлаждения. Обратимый
адиабатический процесс,
называется также изоэнтропийным,
изображается на диаграмме
состояния адиабатой (изоэнтропой).
Молярная
теплоемкость одноатомного газа при
постоянном давлении
(условие
адиабатичности).
Простым примером адиабатического
процесса является сжатие (или расширение)
газа в теплоизолированном цилиндре с
теплоизолированным поршнем: при сжатии
температуpa возрастает, при расширении
- убывает. Другим примером адиабатического
процесса может служить адиабатическое
размагничивание, которое используют
в методе магнитного охлаждения. Обратимый
адиабатический процесс,
называется также изоэнтропийным,
изображается на диаграмме
состояния адиабатой (изоэнтропой).
Молярная
теплоемкость одноатомного газа при
постоянном давлении  . На
плоскости (P, V)
адиабаты изображаются семейством
кривых PV γ =
const. Это соотношение называют уравнением
Пуассона.
Здесь
. На
плоскости (P, V)
адиабаты изображаются семейством
кривых PV γ =
const. Это соотношение называют уравнением
Пуассона.
Здесь  –
показатель адиабаты. Для одноатомного
газа y=5/3 .
–
показатель адиабаты. Для одноатомного
газа y=5/3 .
Теплоёмкость.
Теплоёмкость идеального газа.
Теплоёмкость тела
(обычно обозначается латинской
буквой C) — физическая
величина,
определяющая отношение бесконечно
малого количества
теплотыδQ,
полученного телом, к соответствующему
приращению его температуры δT:![]() Теплоемкость
идеального газа в изопроцессах:
Теплоемкость
идеального газа в изопроцессах:
Адиабатический.В
адиабатическом процессе теплообмена
с окружающей средой не происходит, то
есть ![]() .
Однако, объём, давление и температура
меняются, то есть
.
Однако, объём, давление и температура
меняются, то есть ![]() .Следовательно,
теплоемкость идеального газа в
адиабатическом процессе равна нулю:
.Следовательно,
теплоемкость идеального газа в
адиабатическом процессе равна нулю: ![]() .
.
Изотермический.
В
изотермическом процессе постоянна
температура, то есть ![]() .
При изменении объема газу передается
(или отбирается) некоторое количество
тепла. Следовательно, теплоемкость
идеального газа стремится к бесконечности:
.
При изменении объема газу передается
(или отбирается) некоторое количество
тепла. Следовательно, теплоемкость
идеального газа стремится к бесконечности: ![]()
Изохорный.В
изохорическом процессе постоянен
объем, то есть ![]() .
Элементарная работа газа равна
произведению изменения объема на
давление, при котором происходит
изменение (
.
Элементарная работа газа равна
произведению изменения объема на
давление, при котором происходит
изменение (![]() ).
Первое Начало Термодинамики для
изохорического процесса имеет вид:
).
Первое Начало Термодинамики для
изохорического процесса имеет вид:
![]() .А
для идеального газа
.А
для идеального газа![]() .Таким
образом,
.Таким
образом,
![]() ,
где
,
где ![]() —
число степеней свободы частиц газа.
—
число степеней свободы частиц газа.
Изобарный.В
изобарном процессе
(![]() ):
):
![]()
Количество теплоты. Внутренняя энергия. Первый закон термодинамики. Количество теплоты — энергия, которую получает или теряет тело при теплопередаче. Количество теплоты является одной из основных термодинамических величин. Количество теплоты является функцией процесса, а не функцией состояния, то есть количество теплоты, полученное системой, зависит от способа, которым она была приведена в текущее состояние.Внутренняя энергия тела может изменяться за счет работы внешних сил. Для характеристики изменения внутренней энергии при теплообмене вводится величина, называемая количеством теплоты и обозначаемая Q. Вну́тренняя эне́ргия тела (обозначается как E или U) — это сумма энергий молекулярных взаимодействий и тепловых движений молекулы. Внутренняя энергия является однозначной функцией состояния системы. Это означает, что всякий раз, когда система оказывается в данном состоянии, её внутренняя энергия принимает присущее этому состоянию значение, независимо от предыстории системы. Следовательно, изменение внутренней энергии при переходе из одного состояния в другое будет всегда равно разности между ее значениями в конечном и начальном состояниях, независимо от пути, по которому совершался переход.
Внутреннюю энергию тела нельзя измерить напрямую. Можно определить только изменение внутренней энергии:
![]() ,
где
,
где
![]() —
подведённая к телу теплота,
измеренная в джоулях,
—
подведённая к телу теплота,
измеренная в джоулях,
![]() [1] — работа,
совершаемая телом против внешних сил,
измеренная в джоулях. Первый
закон термодинамики:
Изменение ΔU внутренней
энергии неизолированной термодинамической
системы равно разности между количеством
теплоты Q,
переданной системе, и работой A,
совершенной системой над внешними
телами.
[1] — работа,
совершаемая телом против внешних сил,
измеренная в джоулях. Первый
закон термодинамики:
Изменение ΔU внутренней
энергии неизолированной термодинамической
системы равно разности между количеством
теплоты Q,
переданной системе, и работой A,
совершенной системой над внешними
телами.
|
Соотношение, выражающее первый закон термодинамики, часто записывают в другой форме:
|
В изотермическом процессе температура газа не изменяется, следовательно, не изменяется и внутренняя энергия газа, ΔU = 0. Первый закон термодинамики для изотермического процесса выражается соотношением
|
Количество теплоты Q, полученной газом в процессе изотермического расширения, превращается в работу над внешними телами. При изотермическом сжатии работа внешних сил, произведенная над газом, превращается в тепло, которое передается окружающим телам.
Работа, совершаемая в равновесном процессе. Тезис «работа не есть функция состояния».Равновесным состоянием называется такое термодинамическое состояние системы, которое не изменяется во времени , причем эта неизменяемость не обусловлена протеканием какого-либо внешнего процесса.При устойчивом равновесии любые состояния, смежные с ним, являются менее устойчивыми, и переход к ним из состояния устойчивого равновесия всегда связан с необходимость затраты работы извне. Все необратимые процессы происходят до тех пор, пока не установится равновесие системы, а свидетельствует о том, что работа совершается системой только в том случае, если ею не достигнуто равновесное состояние. В равновесном состоянии термодинамическая система не совершает работу над окружающей средой. Термодинамика работает с функциями состояния, однако среди ее основных понятий имеются два - работа и теплота, - которым, вообще говоря, не соответствуют функции состояния.Понятие работы перекочевало в термодинамику из механики и имеет тот же смысл. Например, при перемещении поршня в цилиндре с газом совершается работа dW, равная произведению силы F на перемещение dh: dW = F dh. Сила, действующая со стороны газа на поршень сечения s, F = ps, где р - давление газа. Таким образом, dW = ps dh = p dV, где dV - изменение объема газа в цилиндре при перемещении поршня на расстояние dh. Суммарная работа, совершенная системой при изменении объема от значения V1 до значения V2 , равна сумме всех элементарных работ на этом пути: Геометрическая интерпретация работы W имеет очень ясный смысл. На pV-графике работа, совершаемая системой, равна заштрихованной площади под кривой I на рис. 1. Если система переходит из состояния 1 в состояние 2 по другому пути, то и совершаемая работа будет другой, так что в общем случае работа, которую выполняет система, зависит от формы пути перехода между начальным и конечным состояниями. Таким образом, работа в термодинамике не является функцией состояния, а dW не есть полный дифференциал функции состояния. В этом отношении простейший случай, рассматриваемый в механике, когда работа не зависит от пути, исключителен. Подчеркнем, что, если бы работа вдоль замкнутого контура всегда была равна нулю, тепловые машины, в которых происходит превращение тепла в работу, были бы невозможны.
Термодинамические тела. Температура. Внутренняя энергия. Макропараметры. Уравнения состояний. Термодинамическое тело, посредством которого в тепловых двигателях осуществляется преобразование теплоты в работу или работы в теплоту, принято называть рабочим телом. Рабочим телом в термодинамике называется газ или иное термодинамическое тело, которое совершает круговой процесс и обменивается энергией с другими телами. Термодинамическая система — это процесс или среда, которая используется при анализе передачи энергии. Термодинамическая система — это любая зона или пространство, ограниченное действительными или воображаемыми границами, выбранными для анализа энергии и ее преобразования. Границы термодинамической системы могут быть неподвижными или подвижными. Температу́ра — скалярная физическая величина, характеризующая приходящуюся на одну степень свободы среднюю кинетическую энергию частиц макроскопической системы, находящейся в состоянии термодинамического равновесия. Вну́тренняя эне́ргия тела (обозначается как E или U) — это сумма энергий молекулярных взаимодействий и тепловых движений молекулы. Внутренняя энергия является однозначной функцией состояния системы. Это означает, что всякий раз, когда система оказывается в данном состоянии, её внутренняя энергия принимает присущее этому состоянию значение, независимо от предыстории системы. Следовательно, изменение внутренней энергии при переходе из одного состояния в другое будет всегда равно разности между ее значениями в конечном и начальном состояниях, независимо от пути, по которому совершался переход.
Внутреннюю энергию тела нельзя измерить напрямую. Можно определить только изменение внутренней энергии: , где — подведённая к телу теплота, измеренная в джоулях, [1] — работа, совершаемая телом против внешних сил, измеренная в джоулях. Эта формула является математическим выражением первого начала термодинамики. Макропараметры — это параметры, характеризующие систему в целом (давления, объёма и температуры). Например, объем V, давление p, средняя скорость молекул , температура T, концентрация n и т.д. Значения этих параметров могут быть установлены с помощью измерительных приборов.
Уравнение
состояния, связывает давление р, объём
V и температуру Т физически однородной
системы в состоянии равновесия
термодинамического: f (p, V, Т) = 0. Это
уравнение называется термическим
Уравнение состояния, в отличие от
калорического Уравнение состояния,
определяющего внутреннюю энергию
системы U как функцию какого-либо двух
из трёх параметров р, V, Т. Термическое
Уравнение состояния позволяет выразить
давление через объём и температуру р
= p (V, Т) и определить элементарную работу
dA = = pdV при бесконечно малом расширении
системы dV. Уравнение состояния является
необходимым дополнением к термодинамическим
законам, которое делает возможным их
применение к реальным веществам. Оно
не может быть выведено с помощью одних
только законов термодинамики, а
определяется или рассчитывается
теоретически на основе представлений
о строении вещества методами статистической
физики. Из первого начала термодинамики
следует лишь существование калорического
Уравнение состояния, а из второго начала
термодинамики – связь между термическим
и калорическим Уравнение состояния
![]()
откуда
вытекает, что для идеального газа
внутренняя энергия не зависит от объёма
![]() = 0. Термодинамика показывает, что для
вычисления как термического, так и
калорического Уравнение состояния,
достаточно знать любой из потенциалов
термодинамических в виде функции своих
параметров. Например, если известна
Гельмгольцева энергия F как функция Т
и V, то Уравнение состояния находят
дифференцированием:
= 0. Термодинамика показывает, что для
вычисления как термического, так и
калорического Уравнение состояния,
достаточно знать любой из потенциалов
термодинамических в виде функции своих
параметров. Например, если известна
Гельмгольцева энергия F как функция Т
и V, то Уравнение состояния находят
дифференцированием:
![]() .
Примерами Уравнение состояния для
газов может служить Клапейрона уравнение
для идеального газа pu = RT, где R – газовая
постоянная, u – объём 1 моля газа.
.
Примерами Уравнение состояния для
газов может служить Клапейрона уравнение
для идеального газа pu = RT, где R – газовая
постоянная, u – объём 1 моля газа.
Колебания. Гармонические колебания. Квазиупругая сила. Колеба́ния — повторяющийся в той или иной степени во времени процесс изменения состояний системы около точки равновесия. Например, при колебаниях маятника повторяются отклонения его в ту и другую сторону от вертикального положения; при колебаниях в электрическом колебательном контуре повторяются величина и направление тока, текущего через катушку.
Колебания почти всегда связаны с попеременным превращением энергии одной формы проявления в другую форму. По физической природе
Механические, Электромагнитные, Смешанного типа — комбинации вышеперечисленных
По характеру взаимодействия с окружающей средой: Вынужденные, Свободные (или собственные). Автоколебания .Параметрические, Случайные. Гармоническое колебание — явление периодического изменения какой-либо величины, при котором зависимость от аргумента имеет характер функции синуса или косинуса. Например, гармонически колеблется величина, изменяющаяся во времени следующим образом:
![]() Или
Или
![]() ,
где х —
значение изменяющейся величины, t время,
остальные параметры — постоянные: А —
амплитуда колебаний, ω —
циклическая частота колебаний,
,
где х —
значение изменяющейся величины, t время,
остальные параметры — постоянные: А —
амплитуда колебаний, ω —
циклическая частота колебаний, ![]() —
полная фаза колебаний,
—
полная фаза колебаний, ![]() —
начальная фаза колебаний. Обобщенное
гармоническое колебание в дифференциальном
виде
—
начальная фаза колебаний. Обобщенное
гармоническое колебание в дифференциальном
виде
![]() Квазиупругая
сила направленная к центру О сила F,
величина которой пропорциональна
расстоянию r от центра О до точки
приложения силы; численно F = cr, где с —
постоянный коэффициент. Тело, находящееся
под действием К. с., обладает потенциальной
энергией П = 1/2cr2. Название «К. с.» связано
с тем, что аналогичным свойством обладают
силы, возникающие при малых деформациях
упругих тел (так называемые силы
упругости). Для материальной точки,
находящейся под действием К. с., центр
О является положением устойчивого
равновесия. Выведенная из этого положения
точка будет совершать около О линейные
Гармонические колебания или описывать
эллипс (в частности, окружность).
Квазиупругая
сила направленная к центру О сила F,
величина которой пропорциональна
расстоянию r от центра О до точки
приложения силы; численно F = cr, где с —
постоянный коэффициент. Тело, находящееся
под действием К. с., обладает потенциальной
энергией П = 1/2cr2. Название «К. с.» связано
с тем, что аналогичным свойством обладают
силы, возникающие при малых деформациях
упругих тел (так называемые силы
упругости). Для материальной точки,
находящейся под действием К. с., центр
О является положением устойчивого
равновесия. Выведенная из этого положения
точка будет совершать около О линейные
Гармонические колебания или описывать
эллипс (в частности, окружность).
Дифференциальное уравнение гармонич. колебаний. Гармонический осциллятор. Дифференциальное уравнение свободных затухающих колебаний линейной системы
![]() ,где
s — колеблющаяся величина, описывающая
тот или иной физический процесс, δ =
const — коэффициент затухания, (ω0 —
циклическая частота свободных
незатухающих колебаний той же
колебательной системы, т. е. при δ =0 (при
отсутствии потерь энергии) называется
собственной частотой колебательной
системы. Гармонический
осциллятор (в классической механике)
— это система, которая при смещении из
положения равновесия испытывает
действие возвращающей силы F
, пропорциональной смещению x
(согласно закону Гука):
,где
s — колеблющаяся величина, описывающая
тот или иной физический процесс, δ =
const — коэффициент затухания, (ω0 —
циклическая частота свободных
незатухающих колебаний той же
колебательной системы, т. е. при δ =0 (при
отсутствии потерь энергии) называется
собственной частотой колебательной
системы. Гармонический
осциллятор (в классической механике)
— это система, которая при смещении из
положения равновесия испытывает
действие возвращающей силы F
, пропорциональной смещению x
(согласно закону Гука):
![]()
Где k — коэффициент жёсткости системы.
Если F — единственная сила, действующая на систему, то систему называют простым или консервативным гармоническим осциллятором. Свободные колебания такой системы представляют собой периодическое движение около положения равновесия (гармонические колебания). Частота и амплитуда при этом постоянны, причём частота не зависит от амплитуды.
Энергия гармонических колебаний. При колебании в момент максимума отклонения хм скорость и потому кинетическая энергия равна нулю, а максимальна потенциальная энергия (положения). При колебании она превращается в кинетическую, увеличивая скорость до максимума, а при уменьшении скорости Ек снова превращается в Еп. Полная механическая энергия равна сумме кинетической и потенциальной, в любой точке, и равна максимума любой из них, для пружиныE=mv2/2+kx2/2=mvo2/2=kxo2/2.Она также пропорциональна квадрату частоты колебаний.Для маятника кинетическая энергия та же, а потенциальная растет с подъемом Еп=mgH, максимальна при Нmax,mgHmax=mvmax2/2. Скорость и кинетическая энергия максимальны в момент прохождения положения равновесия (х=Н=0). Т.о. разные величины достигают максимума в разные моменты, фазы .Из энергии E=mv2/2+kx2/2=mvo2/2=kxo2/2следует x2+(v√m/k)2=Хo2, в прямоугольном треугольнике с катетами х, v√ k/m и гипотенузой хо,x=xosinф – показывает изменение по закону синуса, гармонических колебаний. Аналогичные уравнения и превращения возможны для любых форм энергии, даже когда колебания не видны. В электротехнике важны электрические и электромагнитные колебания, когда электрическая энергия зарядов, конденсатора Ес=СU2/2превращается в энергию тока или его магнитного поля, катушки индуктивностиEi=LI2/2инаоборот, как в маятнике. Изменения электрических величин определяет период собственных колебаний Т= 1/v=2π/w= 2π√LC(формула Томсона).Электрическое и магнитное поле могут порождать друг друга, существовать и передаваться в пространстве без тел, как свет,излучение. Колебания тел и их излучение растут с температурой (тепловые колебания и потери). Равенство этих энергий обеспечивает сохранение, не затухание колебаний. На деле обычные колебания всегда затухают, из-за наличия сил трения, сопротивления и потерь, превращения энергии в другие формы, беспорядочную, тепловую (16.6). Это – проявление закона равнораспределения и рассеяния энергии, 2-го закона ТД.
Физический маятник — осциллятор, представляющий собой твёрдое тело, совершающее колебания в поле каких-либо сил относительно точки, не являющейся центром масс этого тела, или неподвижной оси, перпендикулярной направлению действия сил и не проходящей через центр масс этого тела. Период малых колебаний физического маятника
Если
амплитуда колебаний ![]() мала,
то корень в знаменателе эллиптического
интеграла приближенно равен единице.
Такой интеграл легко берется, и получается
хорошо известная формула малых колебаний:
мала,
то корень в знаменателе эллиптического
интеграла приближенно равен единице.
Такой интеграл легко берется, и получается
хорошо известная формула малых колебаний:
![]() .
Эта формула даёт результаты приемлемой
точности (ошибка менее 1 %) при углах,
не превышающих 4°. Следующий порядок
приближения можно использовать с
приемлемой точностью (ошибка менее
1 %) при углах до 1 радиана (≈60°)
.
Эта формула даёт результаты приемлемой
точности (ошибка менее 1 %) при углах,
не превышающих 4°. Следующий порядок
приближения можно использовать с
приемлемой точностью (ошибка менее
1 %) при углах до 1 радиана (≈60°)
![]() .
.
Затухающие
колебания. Параметры затухания.
Затухающие
колебания —
колебания, энергия которых уменьшается
с течением времени. Бесконечно длящийся
процесс вида ![]() в
природе невозможен. Свободные колебания
любого осциллятора рано или поздно
затухают и прекращаются. Поэтому на
практике обычно имеют дело с затухающими
колебаниями. Они характеризуются тем,
что амплитуда колебаний A является
убывающей функцией. Обычно затухание
происходит под действием сил сопротивления
среды, наиболее часто выражаемых
линейной зависимостью от скорости
колебаний
в
природе невозможен. Свободные колебания
любого осциллятора рано или поздно
затухают и прекращаются. Поэтому на
практике обычно имеют дело с затухающими
колебаниями. Они характеризуются тем,
что амплитуда колебаний A является
убывающей функцией. Обычно затухание
происходит под действием сил сопротивления
среды, наиболее часто выражаемых
линейной зависимостью от скорости
колебаний ![]() или
её квадрата. В акустике: затухание —
уменьшение уровня сигнала до полной
неслышимости.
Пускай
имеется система, состоящая
из пружины (подчиняющейся закону
Гука),
один конец которой жёстко закреплён,
а на другом находится тело массой m.
Колебания совершаются в среде, где сила
сопротивления пропорциональна скорости
с коэффициентом .
Тогда второй
закон Ньютона для
рассматриваемой системы запишется так
или
её квадрата. В акустике: затухание —
уменьшение уровня сигнала до полной
неслышимости.
Пускай
имеется система, состоящая
из пружины (подчиняющейся закону
Гука),
один конец которой жёстко закреплён,
а на другом находится тело массой m.
Колебания совершаются в среде, где сила
сопротивления пропорциональна скорости
с коэффициентом .
Тогда второй
закон Ньютона для
рассматриваемой системы запишется так
![]() где
где ![]() —
сила сопротивления,
—
сила сопротивления, ![]() —
сила упругости
—
сила упругости
![]() ,
, ![]() ,
то есть
,
то есть
![]() или в дифференциальной форме
или в дифференциальной форме
![]() ,где k —
коэффициент упругости в законе
Гука, c —
коэффициент сопротивления, устанавливающий
соотношение между скоростью движения
грузика и возникающей при этом силой
сопротивления.
,где k —
коэффициент упругости в законе
Гука, c —
коэффициент сопротивления, устанавливающий
соотношение между скоростью движения
грузика и возникающей при этом силой
сопротивления.
Для
упрощения вводятся следующие
обозначения: ![]() .
Величину
.
Величину ![]() называют
собственной частотой системы,
называют
собственной частотой системы, ![]() —
коэффициентом затухания. Тогда
дифференциальное уравнение принимает
вид
—
коэффициентом затухания. Тогда
дифференциальное уравнение принимает
вид
![]()
Сделав
замену ![]() ,
получают характеристическое
уравнение
,
получают характеристическое
уравнение
![]() .
Корни которого вычисляются по следующей
формуле
.
Корни которого вычисляются по следующей
формуле
![]() .
В зависимости от величины коэффициента
затухания решение разделяется на три
возможных варианта. Апериодичность
Если
.
В зависимости от величины коэффициента
затухания решение разделяется на три
возможных варианта. Апериодичность
Если ![]() ,
то имеется два действительных корня,
и решение дифференциального уравнения
принимает вид:
,
то имеется два действительных корня,
и решение дифференциального уравнения
принимает вид:
![]() В этом случае колебания с самого начала
экспоненциально затухают. Граница
апериодичности
Если
В этом случае колебания с самого начала
экспоненциально затухают. Граница
апериодичности
Если ![]() ,
два действительных корня совпадают
,
два действительных корня совпадают ![]() ,
и решением уравнения является:
,
и решением уравнения является:
![]() В
данном случае может иметь место
вре́менный рост, но потом —
экспоненциальное затухание. Слабое
затухание Если
В
данном случае может иметь место
вре́менный рост, но потом —
экспоненциальное затухание. Слабое
затухание Если ![]() ,
то решением характеристического
уравнения являются два комплексно
сопряжённых корня
,
то решением характеристического
уравнения являются два комплексно
сопряжённых корня![]() Тогда решением исходного дифференциального
уравнения является
Тогда решением исходного дифференциального
уравнения является
![]() .
Где
.
Где ![]() —
собственная частота затухающих
колебаний.
—
собственная частота затухающих
колебаний.
Константы ![]() и
и ![]() в
каждом из случаев определяются из
начальных условий:
в
каждом из случаев определяются из
начальных условий: ![]()
Вынужденные
колебания. Резонанс. Вынужденные
колебания — колебания, происходящие
под воздействием внешних сил, меняющихся
во времени.
Наиболее
простой и содержательный пример
вынужденных колебаний можно получить
из рассмотрения гармонического
осциллятора и
вынуждающей силы, которая изменяется
по закону: ![]() . —
явление резкого возрастания амплитуды вынужденных
колебаний, которое наступает при
приближении частоты внешнего
воздействия к некоторым значениям
(резонансным частотам), определяемым
свойствами системы. Увеличение
амплитуды — это лишь следствие резонанса,
а причина —
совпадение внешней (возбуждающей)
частоты с внутренней (собственной)
частотой колебательной системы. При
помощи явления резонанса можно выделить
и/или усилить даже весьма слабые
периодические колебания. Резонанс —
явление, заключающееся в том, что при
некоторой частоте вынуждающей силы
колебательная система оказывается
особенно отзывчивой на действие этой
силы.
. —
явление резкого возрастания амплитуды вынужденных
колебаний, которое наступает при
приближении частоты внешнего
воздействия к некоторым значениям
(резонансным частотам), определяемым
свойствами системы. Увеличение
амплитуды — это лишь следствие резонанса,
а причина —
совпадение внешней (возбуждающей)
частоты с внутренней (собственной)
частотой колебательной системы. При
помощи явления резонанса можно выделить
и/или усилить даже весьма слабые
периодические колебания. Резонанс —
явление, заключающееся в том, что при
некоторой частоте вынуждающей силы
колебательная система оказывается
особенно отзывчивой на действие этой
силы.
колебания
в резонансе будут описываться следующим
соотношением:
![]() .
.
Векторная
диаграмма. Сложение гармонических
колебаний. Векторная
диаграмма —
графическое изображение меняющихся
по закону синуса (косинуса) величин и
соотношений между ними при помощи
направленных отрезков — векторов. Векторные
диаграммы можно считать вариантом (и
иллюстрацией) представления колебаний
в виде комплексных
чисел.
При таком сопоставлении ось Ox соответствует
оси действительных чисел, а ось Oy - оси
чисто мнимых чисел.
Тогда
вектор длиной A,
вращающийся в комплексной плоскости
с постоянной угловой скоростью ω с
начальным углом φ0 запишется
как комплексное число
![]() а его действительная часть
а его действительная часть
![]() -есть гармоническое колебание с
циклической частотой ω и
начальной фазой φ0.
Сложение гармонических колебаний
одинаковой частоты
На практике (например, в электротехнике)
часто приходится иметь дело с колебаниями
одинаковой частоты. Любые два таких
колебания можно представить в виде:
-есть гармоническое колебание с
циклической частотой ω и
начальной фазой φ0.
Сложение гармонических колебаний
одинаковой частоты
На практике (например, в электротехнике)
часто приходится иметь дело с колебаниями
одинаковой частоты. Любые два таких
колебания можно представить в виде:
y1 = A1 sin (ωt + φ1) ; y2 = A2 sin (ωt + φ2) . Особый интерес представляет случай, когда начальная фаза первого колебания равна 0, а начальная фаза второго колебания равна π/2. Тогда y1 = A1 sin ωt ; y2 = A2 sin (ωt + π/2) . Сумма таких гармонических колебаний равна: A1 sin ωt + A2 cos ωt = \/A12 + A22 • sin (ωt + φ). (1) где угол φ определяется из условий
![]() (2).
Формула (1) показывает, что если
два гармонических колебания имеют
одинаковую частоту и фазы 0 и π/2,
то их сумма есть гармоническое
колебание той же частоты.
Амплитуда А суммарного
колебания выражается через
амплитуды A1и A2 слагаемых
колебаний по формуле A = \/A12 + A22,а
начальная фаза φ определяется
из условий (2).
(2).
Формула (1) показывает, что если
два гармонических колебания имеют
одинаковую частоту и фазы 0 и π/2,
то их сумма есть гармоническое
колебание той же частоты.
Амплитуда А суммарного
колебания выражается через
амплитуды A1и A2 слагаемых
колебаний по формуле A = \/A12 + A22,а
начальная фаза φ определяется
из условий (2).
Волны. Бегущая косинусоидальная волна. Волна́ — изменение состояния среды или физического поля (возмущение), распространяющееся либо колеблющееся в пространстве и времени или в фазовом пространстве. По своему характеру волны подразделяются на[источник не указан 247 дней]:
По признаку распространения в пространстве: стоячие, бегущие.
По характеру волны: колебательные, уединённые (солитоны).
По типу волн: поперечные, продольные, смешанного типа.
По законам, описывающим волновой процесс: линейные, нелинейные.
По свойствам субстанции: волны в дискретных структурах, волны в непрерывных субстанциях.
По геометрии: сферические (пространственные), одномерные (плоские), спиральные.
Случай одномерного однородного пространства (или одномерной однородной среды)[2] — наиболее прост.
В
этом случае все виды гармонических
волн сводятся к: синусоидальным
(косинусоидальным) бегущим волнам:
![]()
Плоская волна. Волновой вектор. Волновая поверхность и фазовая скорость. плоская волна — плоскости равных фаз перпендикулярны направлению распространения волны и параллельны друг другу; Волны, зависящие от одной пространственной координаты. Описание. В плоской волне всем точкам среды, лежащим в любой плоскости, перпендикулярной направлению распространения волны, в каждый момент времени соответствуют одинаковые смещения и скорости частиц среды. Таким образом, все величины, характеризующие плоскую волну, являются функциями времени и только одной координаты, например, х, если ось Ох совпадает с направлением распространения волны. Волновое уравнение для продольной плоской волны имеет вид: д2j/дx2 = (1/c2)д2j/дt2. (1) Его общее решение выражается следующим образом: j = f1(ct - x)+f2(ct + x), (2), где j - потенциал или другая величина, характеризующая волновое движение среды (смещение, скорость смещения и т.д.); с - скорость распространения волны; f1 и f2 - произвольные функции, причем первое слагаемое (2) описывает плоскую волну, распространяющуюся в положительном направлении оси Ох, а второе - в противоположном направлении. Волновой вектор — вектор, направление которого перпендикулярно фазовому фронту бегущей волны, а абсолютное значение равно волновому числу. Волновой вектор обычно обозначается латинской буквой k и измеряется в обратных
сантиметрах.Волновое
число связано с длиной
волны λ
соотношением:
![]() .
Волновая поверхность - воображаемая
поверхность, до всех точек которой свет
из данного источника доходит одновременно.
Фазовая скорость – это скорость
распространения фазы волны.
Основная
формула, определяющая фазовую скорость
(монохроматической) волны в одномерном
пространстве или фазовую скорость
вдоль волнового вектора для волны в
пространстве большей размерности:
.
Волновая поверхность - воображаемая
поверхность, до всех точек которой свет
из данного источника доходит одновременно.
Фазовая скорость – это скорость
распространения фазы волны.
Основная
формула, определяющая фазовую скорость
(монохроматической) волны в одномерном
пространстве или фазовую скорость
вдоль волнового вектора для волны в
пространстве большей размерности:
![]() .
Итак, скорость
распространения фазы есть скорость
распространения волны. Т.е. υ в уравнении
волны есть фазовая скорость. Для
синусоидальной волны скорость переноса
энергии равна фазовой скорости.
.
Итак, скорость
распространения фазы есть скорость
распространения волны. Т.е. υ в уравнении
волны есть фазовая скорость. Для
синусоидальной волны скорость переноса
энергии равна фазовой скорости.
В общем случае волновое уравнение записывается в виде
![]() ,
,
где ![]() — оператор
Лапласа,
— оператор
Лапласа, ![]() —
неизвестная функция,
—
неизвестная функция, ![]() —
время,
—
время, ![]() —
пространственная переменная,
—
пространственная переменная, ![]() — фазовая
скорость.
— фазовая
скорость.
В одномерном случае уравнение называется также уравнением колебания струны и записывается в виде
![]() .
.
Энергия
волны. Интенсивность. Сферическая
волна. Распространение
механической волны, представляющее
собой последовательную передачу
движения от одного участка среды к
другому, означает тем самым передачу
энергии. Эту энергию доставляет источник
волны, когда он приводит в движение
непосредственно прилегающий к нему
слой среды. От этого слоя энергия
передается следующему слою и т. д. Таким
образом, распространение волны создает
в среде поток энергии, расходящийся от
источника.
Интенси́вность — скалярная физическая
величина,
количественно характеризующая мощность,
переносимую волной в
направлении распространения. Численно
интенсивность равна усреднённой
за период
колебаний волны
мощности излучения, проходящей через
единичную площадку,
расположеннуюперпендикулярно направлению
распространения энергии. В математической
форме это может быть выражено следующим
образом:
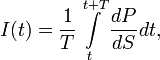
где T —
период волны, dP —
мощность, переносимая волной через
площадку dS.
Интенсивность волны связана со
средней плотностью
энергии w в
волне и скоростью распространения
волны u следующим
соотношением:
![]() сферическая волна
— поверхностью равных фаз является сфера;
Волны, возбуждаемые точечным источником.
Описание
сферическая волна
— поверхностью равных фаз является сфера;
Волны, возбуждаемые точечным источником.
Описание
Для сферической волны потенциал j и другие величины, характеризующие волновое движение среды (смещение, скорость смещения) зависят только от времени и расстояния r от некоторой точки пространства, называемой центром волны. Сферические волны возбуждаются в однородной и изотропной среде точечным источником - колеблющимся телом, размеры которого малы по сравнению с расстоянием до рассматриваемых точек среды.
Волновое уравнение для продольной сферической волны: (1/r2)д(r2дj/дr)/дr = (1/c2) д2j/дt2. (1) Общее решение (1) имеет вид: j = (1/r)f1(ct - r)+(1/r)f2(ct + r), (2) где f1 и f2 - произвольные функции, причем первое слагаемое (2) описывает потенциал для расходящейся сферической волны, а второе - потенциал для сферической волны, сходящейся к центру.При распространении сферической волны ее волновые поверхности (геометрическое место точек среды, в которых фаза волны в рассматриваемый момент времени имеет одно и то же значение) представляют собой систему концентрических сфер.
Стоячая волна. Стоячая волна это возникающий в результате колебательный процесс. Практически стоячие волны возникают при отражении волн от преград. Падающая на преграду волна и бегущая ей навстречу отраженная волна, налагаясь друг на друга, дают стоячую волну. Уравнение стоячей волны Напишем уравнения двух плоских волн, распространяющихся вдоль оси х в противоположных направлениях:
 Сложив
вместе эти уравнения и преобразовав
результат по формуле для суммы косинусов,
получим уравнение
стоячей волны:
Сложив
вместе эти уравнения и преобразовав
результат по формуле для суммы косинусов,
получим уравнение
стоячей волны:
![]() Преобразовав
это уравнение, получим упрощенное
уравнение стоячей волны:
Преобразовав
это уравнение, получим упрощенное
уравнение стоячей волны:
![]()
Сложение скоростей. Преобразования Галилея. Абсолютное время в классич. Механике и идея дальнодействия.
В
классической механике: V=υ+υ'
Скорость
движения тела относительно неподвижной
системы отсчёта равна векторной сумме
скорости этого тела относительно
подвижной системы отсчета и скорости
самой подвижной системы отсчета
относительно неподвижной системы.
В релятивистской механике формула
сложения скоростей: V=υ+υ'/1+(υυ'/c2)
Где для обеих формул υ и υ' - составляющие
скорости V - результирующая скорость.
с - скорость света в вакууме. Если
ИСО S движется относительно
ИСО S' с
постоянной скоростью ![]() вдоль
оси
вдоль
оси ![]() ,
а начала
координат совпадают
в начальный момент времени в обеих
системах, то преобразования Галилея
имеют вид:
,
а начала
координат совпадают
в начальный момент времени в обеих
системах, то преобразования Галилея
имеют вид:
![]()
![]()
![]()
![]() или,
используя векторные обозначения,
или,
используя векторные обозначения,
![]() (последняя
формула остается верной для любого
направления осей координат). Как видим,
это просто формулы для сдвига начала
координат, линейно зависящего от времени
(подразумеваемого одинаковым для всех
систем отсчета).
(последняя
формула остается верной для любого
направления осей координат). Как видим,
это просто формулы для сдвига начала
координат, линейно зависящего от времени
(подразумеваемого одинаковым для всех
систем отсчета).
Из
этих преобразований следуют соотношения
между скоростями движения точки и её
ускорениями в обеих системах отсчета:
![]()
![]() Преобразования Галилея являются
предельным (частным) случаем преобразований
Лоренца для
малых скоростей
Преобразования Галилея являются
предельным (частным) случаем преобразований
Лоренца для
малых скоростей ![]() (много
меньше скорости света).
Физические
тела движутся во времени и пространстве.
Через их движения проявляются свойства
времени и пространства. Время и
пространство определяют самый характер
движений, изучаемых классической
механикой.Вот что классическая механика
говорит нам о свойствах времени.1. Время
существует само по себе н своим
существованием не обязано чему бы то
ни было в мире. 2. Ходу времени подчиняются
все тела природы, все физические явления.
Но сами эти тела и явления не оказывают
никакого воздействия на ход времени.
3. Все моменты времени между собой
равноправны и одинаковы: время однородно.
4. Ход времени всюду и везде в мире
одинаков. 5. Ход времени одинаково
равномерен в прошлом, настоящем и
будущем.6. Время простирается от
настоящего неограниченно назад в
прошлое и неограниченно вперед в
будущее.7. Время обладает одним измерением.
8. Промежутки времени отмеряются,
складываются и вычитаются, как отрезки
евклидовой прямой. Согласно
концепции дальнодействия, тела действуют
друг на друга без материальных
посредников, через пустоту, на любом
расстоянии. Такое взаимодействие
осуществляется с бесконечно большой
скоростью (но подчиняется определённым
законам). Примером силы, считавшейся
одним из примеров непосредственного
действия на расстоянии, можно считать
силу всемирного
тяготения в
классической теории гравитации Ньютона.
(много
меньше скорости света).
Физические
тела движутся во времени и пространстве.
Через их движения проявляются свойства
времени и пространства. Время и
пространство определяют самый характер
движений, изучаемых классической
механикой.Вот что классическая механика
говорит нам о свойствах времени.1. Время
существует само по себе н своим
существованием не обязано чему бы то
ни было в мире. 2. Ходу времени подчиняются
все тела природы, все физические явления.
Но сами эти тела и явления не оказывают
никакого воздействия на ход времени.
3. Все моменты времени между собой
равноправны и одинаковы: время однородно.
4. Ход времени всюду и везде в мире
одинаков. 5. Ход времени одинаково
равномерен в прошлом, настоящем и
будущем.6. Время простирается от
настоящего неограниченно назад в
прошлое и неограниченно вперед в
будущее.7. Время обладает одним измерением.
8. Промежутки времени отмеряются,
складываются и вычитаются, как отрезки
евклидовой прямой. Согласно
концепции дальнодействия, тела действуют
друг на друга без материальных
посредников, через пустоту, на любом
расстоянии. Такое взаимодействие
осуществляется с бесконечно большой
скоростью (но подчиняется определённым
законам). Примером силы, считавшейся
одним из примеров непосредственного
действия на расстоянии, можно считать
силу всемирного
тяготения в
классической теории гравитации Ньютона.
Постулаты Энштейна. Преобразование Лоренца. Относительность одновременности.
Постулаты Эйнштейна :
1. Принцип относительности.
2. Независимость скорости света от скорости источника.
Первый постулат (принцип) указывает на инвариантность законов природы и уравнений их описывающих при переходе из одной инерциальной системы отчета в другую. То есть все ИСО не различимы по своим свойствам, ни какими опытами нельзя выделить ни одну из них как предпочтительную.
Второй постулат (принцип) утверждает, что скорость света в вакууме одинакова во всех направлениях и не зависит от скорости движения источника света. Отсюда следует, что она должна быть предельной и одинаковой во всех инерциальных системах отчета.
Преобразование Лоренца. Лоренц установил связь между координатами и временем события в системах отсчета k и k,' основываясь на тех экспериментальных фактах, что:
все инерциальные системы отсчета физически эквивалентны;
скорость света в вакууме постоянна и конечна во всех инерциальных системах отсчета и не зависит от скорости движения источника и наблюдателя.
Таким образом, при больших скоростях движения сравнимых со скоростью света, Лоренц получил:
|
(8.3.2) |
|
где β = v/c. Это и есть знаменитые преобразования Лоренца. Истинный физический смысл этих формул был впервые установлен Эйнштейном в 1905 г. в СТО. В теории относительности время иногда называют четвертым измерением. Точнее говоря, величина ct, имеющая ту же размерность, что и x, y, z, ведет себя как четвертая пространственная координата. В теории относительности ct и x проявляют себя с математической точки зрения сходным образом. Полученные уравнения связывают координаты и время в подвижной k' и неподвижной k системах отсчета. Отличие состоит только в знаке скорости υ, что и следовало ожидать, поскольку система k' движется относительно k слева направо со скоростью υ, но наблюдатель в системе k' видит систему k, движущуюся относительно него справа налево со скоростью минус υ. При малых скоростях движения (v << c) или при бесконечной скорости распространения взаимодействий (c = ∞, теория дальнодействия) преобразования Лоренца переходят в преобразования Галилея (принцип соответствия).
любая "относительность" означает, что величина или явление зависит от системы отсчета. В частности "относительность одновременности" означает, что события, которые в одной ИСО одновременны, в другой ИСО могут происходить неодновременно. Единое «настоящее», то есть часы, синхронно идущие в различных точках пространства, можно ввести только в рамках конкретной инерциальной системы отсчёта. Однако, этого нельзя сделать одновременно для двух различных систем отсчёта.
Преобразование
длин отрезков и временных промежутков.
Рассмотрим теперь два наиболее важных
следствия специальной теории
относительности - сокращение длины
(лоренцево сокращение длины) и замедление
течения времени. Стержень
длинойl в K «упирается»
в начало координат О и заканчивается
в х (рис.![]() ).
Чему равна длина стержня в K'?
Наблюдатель в K' производит
это измерение, определяя время, за
которое начало его системы О' проходит
вдоль стержня. Этот интервал времени
отсчитывается им от момента, когда
начала координат О и О' совпадают,
т.е. t1 =
0 и
).
Чему равна длина стержня в K'?
Наблюдатель в K' производит
это измерение, определяя время, за
которое начало его системы О' проходит
вдоль стержня. Этот интервал времени
отсчитывается им от момента, когда
начала координат О и О' совпадают,
т.е. t1 =
0 и ![]() .
В момент, когда начало О',
двигаясь со скоростью
.
В момент, когда начало О',
двигаясь со скоростью ![]() ,
достигает конца стержня, часы в
системе K показывают
t2 ,
а в системе K' -
,
достигает конца стержня, часы в
системе K показывают
t2 ,
а в системе K' - ![]() .
Наблюдатель K видит,
что начало строения прошло путь l со
скоростью v,
так что t2 = l/v.
Интервал времени, измеренный в K',
.
Наблюдатель K видит,
что начало строения прошло путь l со
скоростью v,
так что t2 = l/v.
Интервал времени, измеренный в K',
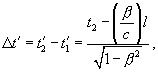 (1.4.6)
(1.4.6)
как
это следует из (1.4.4)
и условий ![]() .
Учитывая, что t2 =
l/v, мы получим
.
Учитывая, что t2 =
l/v, мы получим
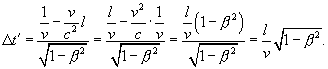 (1.4.7)
(1.4.7)
Умножая это выражение слева и справа на v и замечая, что v*∆t равно l' - длине с точки зрения наблюдателя в K', мы получим теперь, чему же равна длина отрезка l' в движущейся системе K':
![]() (1.4.8)
(1.4.8)
Соотношение (1.4.8) означает, что наблюдатель K', движущийся относительно стержня, увидит его более коротким по сравнению с тем, что видит наблюдатель K, покоящийся относительно стержня. На забываем, конечно, что это справедливо лишь для , близких к скорости света .
При таких скоростях будет происходить и замедление течения времени. Не останавливаясь на деталях этого доказательства, заметим, что оказывается время в движущейся системе тоже изменяется:
![]() (1.4.9)
(1.4.9)
Интервал времени t', отсчитываемый по часам в системе K', оказывается с точки зрения наблюдателя в системе K продолжительнее интервала t, отсчитанного по его собственным часам. Отсюда мы можем сделать вывод, что для любого наблюдателя движущиеся относительно него часы идут медленнее таких же, но покоящихся в его системе часов.
Преобразование скоростей в рел. Механике
Внутри корабля перемещение dx' за время dt' равно dx' = υ' dt' . Найдем dx и dt с точки зрения наблюдателя на Земле, исходя из преобразований Лоренца:
![]() dy = dy',
dz = dz',
dy = dy',
dz = dz',
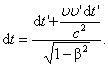 Так как
Так как ![]() ,
то
,
то
|
|
(8.4.8) |
|
Эта формула выражает правило сложения скоростей в релятивистской кинематике.
Интервал. События как точки пространственно-временного континиума. Интервал в теории относительности — расстояние между двумя событиями в пространстве-времени, являющееся обобщением евклидового расстояния между двумя точками. пространство и время определяются теми процессами, событиями, которые в них возникают и существуют. Поэтому самое простое представление о реальности — это представление о том, что мир есть множество (континуум) событий, которое имеет четыре измерения: три из них пространственные, а четвертое — время. Хотя время — это такая же координата, как и любая из трех пространственных, но все же она характеризует континуум с точки зрения направленности его изменений, в то время как пространственные координаты характеризуют сосуществование его событий. Вселенная является трёхмерным или пространственным континуумом.Чтобы полностью описать какое-то событие нужно как минимум указать время и место где оно произошло, место укажет нам пространственный континуум, а добавив время мы получим пространственно-временной континуум. пространство и время определяются теми процессами, событиями, которые в них возникают и существуют. Поэтому самое простое представление о реальности – представление о том, что мир есть множество (континуум) событий, которое имеет четыре измерения: три из них пространственные, а четвертое – время.

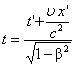 ,
,
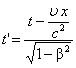 ,
,