36. Касательная плоскость и нормаль к поверхности. Геометрический смысл.

Уравнение F(x,y,z)=0 задает поверхность в трехмерном пространстве. Точка М (x₀,y₀,z₀) принадлежит этой поверхности, если для её координат выполняется неравенство F(x₀,y₀,z₀)=0.

Чтобы найти уравнения касательной плоскости и нормали (перпендикуляра к касательной плоскости) к поверхности в заданной точке М, прежде всего, следует найти частные производные функции F в этой точке:

, , (предполагается, что хотя бы одно из чисел А, В и С отлично от 0).

Тогда уравнения касательной плоскости и нормали к поверхности будут иметь вид:

Уравнение касательной:

Нормали:

Геометрический смысл: частные производные 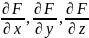равны тангенсу угла наклона касательной к поверхности.

37.Производная по направлению.

z=f(M) с направляющими косинусами {cosα; cosβ}.

Тогда если z диффиринцируемая функция, то можно найти производную от z по направлению вектора .

Производная по направлению нужна дл того, чтобы оценить скорость изменения функции в направлении .

38. Градиент. Направление градиента.

Градиентом функции z=f(M) называется вектор .

Самая большая производная по направлению достигается в направлении градиента функции, т е в .

39. Частные производные высших порядков. Дифференциалы высших порядков.

Частная производная:

Частные производные второго порядка:

Частные производные n-го порядка:

Дифференциал высших порядков: =

40.Экстремум функции двух переменных. Необходимые и достаточные условия существования экстремума.

z=f(x,y) определена на {M}, дифференцируема и

1. Если ∆>0 и в стационарной точке – min

2. Если ∆>0 и в стационарной точке - max

3. Если ∆<0 – экстремума нет

4. Если ∆=0 – требуются дополнительные исследования.

41.Двойной интеграл. Геометрический смысл двойного интеграла.

G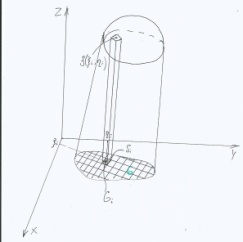 - замкнутая ограниченная область.

Разобьем область G на {G_i} i=1,2,3,…,n.

G_i не имеют общих неграничных точек.

Внутри G_i взята точка (ζ_i,η_i) i=1…n.

Рассмотрим

S_i – площадь G_i

λ- max диаметр областей G_i

Если не зависящей от разбиения G_i, то говорят,

Геометрический смысл двойного интеграла – объём цилиндрической фигуры, ограниченной снизу областью определения G, а сверху функцией z=f(x,y)

42. Основные свойства двойного интеграла.

1)

2)

3)

Необходимое условие существования двойного интеграла: если двойной интеграл существует, то функция непрерывна.

Достаточное условие: если функция непрерывна на области G, то она интегрируема.

G – замкнутая, ограниченная область.

43) Выражение двойного интеграла через повторный.

Пусть   функция двух переменных, интегрируемая по Риману на прямоугольнике  , то есть  . Тогда

где интеграл в левой части двумерный, а остальные повторные одномерные.

Доказательство: Любое разбиение   множества   получено некоторыми разбиениями   отрезка   и   отрезка  , при этом объём любого прямоугольника   определяется  , где   ― некоторые частичные отрезки разбиений. Тогда рассмотрим следующие оценки интеграла   и нижних и верхних интегральных сумм функции   и  : Тогда при интегрируемости   по  , то есть равенстве   из вышеуказанных оценок интеграл   также существует и имеет такое же значение, как и