Осевой момент инерции

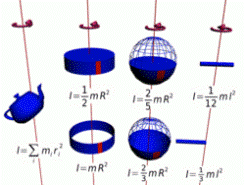
Осевые моменты инерции некоторых тел.

Моментом инерции механической системы относительно неподвижной оси («осевой момент инерции») называется величина J_a, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси:

,

где:

• m_i — масса i-й точки,

• r_i — расстояние от i-й точки до оси.

Осевой момент инерции тела J_a является мерой инертности тела во вращательном движении вокруг оси подобно тому, как масса тела является мерой его инертности в поступательном движении.

,

где:

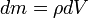•  — масса малого элемента объёма тела  ,

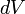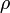•  — плотность,

•  — расстояние от элемента   до оси a.

Если тело однородно, то есть его плотность всюду одинакова, то

35 вопрос. 1. Понятие кинетического момента (или момента количества движения) тесно связано с понятием момента силы и определяется аналогичным образом.

Кинетическим моментом  материальной точки относительно некоторого центра О называется векторная величина, равная векторному произведению радиус-вектора, определяющего положение этой точки относительно центра О, на количество движения точки (рис. 3.8). 

  .

 

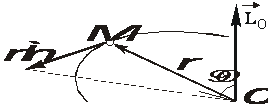
 Рис. 3.8. К определению кинетического момента точки.

Кинетическим моментом механической системы относительно центра О называется геометрическая сумма кинетических моментов всех точек системы относительно того же центра:

  , ( k = 1, 2, ..., n ).

Для определения кинетического момента системы относительно координатных осей, проходящих через центр О, спроектируем векторное равенство (3.28) на эти оси так, как это было сделано при выводе выражений (1.3) в статике: 

   (3.29) 

36 вопрос. Работа силы. Мощность.

Для характеристики действия, оказываемого силой на тело при некотором его перемещении, вводится понятие о работе силы.

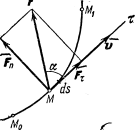
Рис.16

При этом работа характеризует то действие силы, которым определяется изменение модуля скорости движущейся точки.

Введём сначала понятие об элементарной работе силы на бесконечно малом перемещении ds. Элементарной работой силы (рис.16) называется скалярная величина:

,

где - проекция силы на касательную к траектории, направленную в сторону перемещения точки, а -бесконечно малое перемещение точки, направленное вдоль этой касательной.

Данное определение соответствует понятию о работе, как о ха­рактеристике того действия силы, которое приводит к изменению модуля скорости точки. В самом деле, если разложить силу на составляющие и , то изменять модуль скорости точки будет только составляющая , сообщающая точке касательное ускорение Составляющая же или изменяет направление вектора скорости v (сообщает точке нормальное ускорение), или, при несвободном дви­жение изменяет давление на связь. На модуль скорости составляю­щая влиять не будет, т.е., как говорят, сила «не будет про­изводить работу».

Замечая, что , получаем:

. (1)

Таким образом, элементарная работа силы равна проекции силы на направление перемещения точки, умноженной на элементар­ное перемещение или элементарная работа силы равна произведению модуля силы на элементарное перемещение и на косинус угла между направлением силы и направлением перемещения.

Если угол острый, то работа положительна. В частности, при элементарная работа .

Если угол тупой, то работа отрицательна. В частности, при элементарная работа .

Если угол , т.е. если сила направлена перпендикулярно перемещению, то элементарная работа силы равна нулю.

Найдем аналитическое выражение элементарной работы. Для этого разложим силу на составляющие , , по направлениям координатных осей (рис.17; сама сила на чертеже не показана).

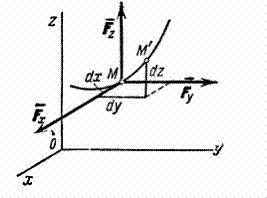
Рис.17

Элементарное перемещение слагается из перемещений , , вдоль координатных осей, где x, y, z - координаты точки М. Тогда работу силы на перемещении можно вычислить как сумму работ её составляющих , , на перемещениях , , .

Но на перемещении совершает работу только составляющая , причем её работа равна . Работа на перемещениях и вычисляется аналогично. Окончательно находим: .

Формула дает аналитическое выражение элементарной работы силы.

Работа силы на любом конечном перемещении М₀М₁ вычисляется как интегральная сумма соответствующих элементарных работ и будет равна:

или

.

Следовательно, работа силы на любом перемещении М₀М₁ равна взятому вдоль этого перемещения интегралу от элементарной работы. Пределы интеграла соответствуют значениям пере­менных интегрирования в точках М₀ и М₁.

Рис.18

Если величина постоянна ( = const), то и обозначая перемеще­ние М₀М₁ через получим: .

Такой случай может иметь место, когда действующая сила постоянна по модулю и направлению (F= const), а точка, к ко­торой приложена сила, движется прямолинейно (рис.18}. В этом случае и работа силы .

Единицей измерения работы в системе СИ является джоуль (1 дж= 1 hm).

Теорема об изменении кинетической энергии точки.

Рассмотрим точку с массой т, перемещающуюся под действием при­ложенных к ней сил из положения M₀ , где она имеет скорость , в положение М₁ , где ее скорость равна .

Для получения искомой зависимости обратимся к уравнению выражающему основной закон динамики. Проектируя обе части этого равенства на касательную к траектории точ­ки М, направленную в сторону движения, получим:

Стоящую слева величину касательного ускорения можно пред­ставить в виде

.

В результате будем иметь:

.

Умножив обе части этого равенства на ds, внесем т под знак дифференциала. Тогда, замечая, что где - эле­ментарная работа силы F_k получим выражение теоремы об изме­нении кинетической энергии в дифференциальной форме:

.

Проинтегрировав теперь обе части этого равенства в пределах, соответствующих значениям переменных в точках M₀ и M₁, найдем окончательно:

.

Уравнение выражает теорему об изменении кине­тической энергии точки в конечном виде: изменение кинетической энергии точки при некотором ее перемещении равно алгебраической сумме работ всех действующих на точку сил на том же перемещении.

41 вопрос. Явление при котором скорости точек тела за очень короткий промежуток времени тау изменяются на конечную величину ,называется ударом. Силы при действии которых происходит удар будем называть ударными силами,время за которое произошел удар будем называть временем удара.

Величина К, равная при прямом ударе тела о неподвижную преграду отношению модуля скорости тела в конце удара к модулю скорости в начале удара, называется коэффициентом восстановления при ударе К=U/V. В качестве придельных случаев рассматривают случай абсолютно упругого удара К=1,при котором кинетическая энергия полностью восстанавливается и случай абсолютно неупругого удара К=0 когда удар заканчивается в первой стадии и вся кинетическая энергия теряется.

42 вопрос. ОСНОВНЫЕ ТЕОРЕМЫ ДИНАМИКИ ПРИ УДАРЕ

ТЕОРЕМА КОЛИЧЕСТВА ДВИЖЕНИЯ: изменение количества движения системы при ударе   равно геометрической сумме внешних ударов  , полученных точками системы при ударе:

ТЕОРЕМА О ДВИЖЕНИИ ЦЕНТРА МАСС: изменение скорости центра масс системы   при ударе равно сумме внешних ударов  , приложенных к системе, деленной на массу всей системы М;

ТЕОРЕМА МОМЕНТОВ КОЛИЧЕСТВА ДВИЖЕНИЯ: изменение при ударе момента количества движения системы относительно точки (оси) равно сумме моментов внешних ударов относительно той же точки (оси):

43 вопрос. КАРНО ТЕОРЕМА в теории удара - кинетич. энергия, потерянная системой при абсолютно неупругом ударе ,равна той кинетич. энергии, к-рую имела бы система, если бы её точки двигались с потерянными скоростями:    где   - кинетич. энергии системы в начале и в конце удара соответственно, m_i - массы точек системы, v_i и u_i - их скорости в начале и в конце удара (разность v_i-u_i наз. потерянной скоростью). Назв. по имени Н. Л. С. Карно. Равенство (*) можно получить как следствие теоремы об изменении кол-ва движения при ударе и условия того, что удар является абсолютно неупругим. Помимо установления наглядного энергетич. соотношения К. т. позволяет в ряде случаев определять скорости тел после неупругого удара. С. М. Таре.

44 вопрос. Центр удара

Центр удара, точка тела, имеющего неподвижную ось вращения, обладающая тем свойством, что удар, направленный в эту точку перпендикулярно к плоскости, проходящей через ось вращения и центр масс тела, не передаётся на ось и не оказывает ударных воздействий на подшипники, в которых эта ось закреплена. Ц. у. всегда существует у тела, имеющего плоскость симметрии, перпендикулярную к оси вращения, и лежит в этой плоскости на расстоянии h = I/Ma от оси вращения, где М — масса тела, / — его момент инерции относительно оси вращения, а — расстояние центра масс тела от этой оси. Вращающиеся ударные устройства (маятниковые копры, курки охотничьих ружей и т.п.) конструируют так, чтобы точка, которой производится удар, была по отношению к оси вращения Ц. у.