
- •10) Геометрические приложения определённого интеграла: площади плоских фигур, длина кривых. Вычисление объёма тел, в том числе тел вращения.
- •11) Числовые ряды. Критерий Коши сходимости числового ряда. Следствие: необходимое условие сходимости ряда.
- •19. (Формула Коши-Адамара),
- •2 5. Определение двойного интеграла и его основные свойства.
- •Сведение двойного интеграла к повторному.
- •26. Тройной интеграл, сведение его к повторному.
- •27, Замена переменных в двойном интеграле. Пример: случай полярных координат.
- •28. Замена переменных в тройном интеграле. Примеры: случаи цилиндрических и сферических координат.
- •29. Вычисление площади гладкой поверхности, заданной параметрически и в явном виде. Элемент площади поверхности.
- •30. О пределение криволинейного интеграла первого рода, его основные свойства и вычисление.
- •Определение криволинейного интеграла второго рода, его основные свойства и вычисление. Связь с интегралом первого рода.
- •31. Формула Грина. Условия того, что криволинейный интеграл на плоскости не зависит от пути интегрирования.
- •32. О пределение поверхностного интеграла первого рода, его основные свойства и вычисление.
- •33. Теорема Гаусса-Остроградского, её запись в координатной и векторной (инвариантной) формах.
- •34. Теорема Стокса, её запись в координатной и векторной (инвариантной) формах.
- •35. Скалярное поле. Градиент скалярного поля и его свойства. Вычисление градиента в декартовых координатах.
- •Поток векторного поля через поверхность. Определение дивергенции векторного поля и её свойства. Вычисление дивергенции в декартовых координатах.
- •Соленоидальные векторные поля, условия соленоидальности.
- •Циркуляция векторного поля и ротор векторного поля. Вычисление ротора в декартовых координатах.
- •36. Оператор Гамильтона (набла), дифференциальные операции второго порядка, связь между ними.
- •37. Основные понятия, относящиеся к оду первого порядка: общее и частное решения, общий интеграл, интегральные кривые. Задача Коши, её геометрический смысл.
- •38. Интегрирование оду первого порядка с разделяющимися переменными и однородных.
- •39. Интегрирование линейных оду первого порядка и уравнений Бернулли.
- •40. Интегрирование оду первого порядка в полных дифференциалах. Интегрирующий множитель.
37. Основные понятия, относящиеся к оду первого порядка: общее и частное решения, общий интеграл, интегральные кривые. Задача Коши, её геометрический смысл.
Дифференциальным
уравнением
называется соотношение ![]() ,
в котором x
– независимая переменная, y
– искомая функция. Это обыкновенное
дифференциальное уравнение
(ОДУ) первого порядка.
,
в котором x
– независимая переменная, y
– искомая функция. Это обыкновенное
дифференциальное уравнение
(ОДУ) первого порядка.
![]() – уравнение,
разрешённое относительно производной.
– уравнение,
разрешённое относительно производной.
![]()
f(x,y) – заданная, непрерывная в некоторой области D переменных (x,y) функция.
П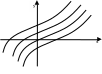 усть
усть
![]() .
График функции
.
График функции ![]() называется интегральной
кривой,
– изоклины
кривые.
называется интегральной
кривой,
– изоклины
кривые.
Пусть правая часть
уравнения (*) не зависит от y,
то есть ![]() ,
тогда
,
тогда ![]() .
.
На рисунке представлено семейство интегральных кривых, зависящих от одного параметра C.
Пусть ![]() .
Будем считать независимой переменной
y,
а x
– функция от y,
то есть
.
Будем считать независимой переменной
y,
а x
– функция от y,
то есть ![]() .
Тогда
.
Тогда ![]() .
Но если
.
Но если ![]() и это уравнение имеет корень
и это уравнение имеет корень ![]() ,
то добавляется решение, которое надо
добавить к общему семейству, зависящему
от параметра C.
,
то добавляется решение, которое надо
добавить к общему семейству, зависящему
от параметра C.
Всякая функция
вида ![]() при подстановке в (*), после чего (*)
становится тождеством, является решением
(общим
решением дифференциального уравнения
(*)).
при подстановке в (*), после чего (*)
становится тождеством, является решением
(общим
решением дифференциального уравнения
(*)).
Если C
взято равным конкретному числу, то
решение φ(x,C0)
называется частным
решением уравнения
(*). ![]() - отсюда находится значение C.
- отсюда находится значение C.
У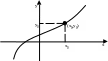 словие
Коши – когда
указано, какому x0
соответствует y0.
Задача Коши:
словие
Коши – когда
указано, какому x0
соответствует y0.
Задача Коши:
![]() – условие уравнения + условие Коши, то
есть
– условие уравнения + условие Коши, то
есть ![]() .
Задачу Коши геометрически можно
сформулировать так: среди всех интегральных
кривых уравнения (*) найти ту кривую
(рисунок слева), которая проходит через
заданную точку (x0,
y0).
.
Задачу Коши геометрически можно
сформулировать так: среди всех интегральных
кривых уравнения (*) найти ту кривую
(рисунок слева), которая проходит через
заданную точку (x0,
y0).
Пример.
Дано: ![]() и
.
Решить задачу Коши.
и
.
Решить задачу Коши.
![]()
Когда ![]() ,
то
:
,
то
:
![]()
![]()
![]() – частное решение задачи Коши.
– частное решение задачи Коши.
38. Интегрирование оду первого порядка с разделяющимися переменными и однородных.
Уравнением с
разделенными переменными
называется
дифференциальное уравнение вида: ![]() с непрерывными функциями f(х)
и g(y).
Равенство
с непрерывными функциями f(х)
и g(y).
Равенство ![]() ,
где C
— произвольная постоянная, определяет
общий интеграл
уравнения с разделёнными переменными.
,
где C
— произвольная постоянная, определяет
общий интеграл
уравнения с разделёнными переменными.
Принцип решения
таких
уравнений: ![]()
![]()
![]()
![]()
Если дано условие
Коши, то есть
и
,
то![]() .
Если
.
Если ![]() и уравнение имеет корень
,
то это решение добавляется к основному
семейству.
и уравнение имеет корень
,
то это решение добавляется к основному
семейству.
Определение
однородной функции.
Функция f(x,y)
называется однородной
функцией
своих переменных x
и y,
если, каково бы ни было число ![]() ,
выполняется следующее:
,
выполняется следующее: ![]() ,
где p
– степень
(показатель) однородности.
Например,
,
где p
– степень
(показатель) однородности.
Например, ![]() – однородная функция, степень однородности
– однородная функция, степень однородности
![]() ,
так как
,
так как ![]() .
Степень p
может быть равной нулю, если
.
Степень p
может быть равной нулю, если ![]() .
.
Уравнение
называется однородным,
если функция, стоящая в правой части,
является однородной функцией своих
переменных. Пусть f(x,y)
будет однородной функцией степени 0, то
есть
.
Пусть ![]() ,
тогда
,
тогда ![]() .
Уравнения такого типа решаются заменой
(переходом к новой функции):
.
Уравнения такого типа решаются заменой
(переходом к новой функции): ![]() .
.
![]()
![]()
![]()
![]()
![]()
![]() – общее решение.
– общее решение.
Если ![]() ,
а
,
а ![]() ,
то:
,
то: ![]()
![]()
![]()
![]()
![]()
Если ![]() ,
то уравнение
имеет корень u0,
тогда:
,
то уравнение
имеет корень u0,
тогда: ![]() – решение:
– решение:
![]() – прямая
наряду с семейством.
– прямая
наряду с семейством.
Общий вид
однородного уравнения,
если его записать в
виде дифференциалов:
![]()
![]()
То есть M(x,y) и N(x,y) должны быть однородными функциями одной и той же степени однородности.
39. Интегрирование линейных оду первого порядка и уравнений Бернулли.
ДУ первого
порядка
называется линейным,
если неизвестная функция y(x)
и её производная y’(x)
входят в уравнение в первой степени:
![]() .
P(x),
Q(x)
– непрерывные функции. Уравнение
однородное,
если Q(x)=0.
.
P(x),
Q(x)
– непрерывные функции. Уравнение
однородное,
если Q(x)=0.
Форма вариации
производной постоянной: ![]() (1),
обнуляем
правую часть
(1),
обнуляем
правую часть ![]()
![]() . Общее решение уравнения:
. Общее решение уравнения:![]() .
Находим
производную
.
Находим
производную ![]() .
Подставим y
и y’
в уравнение (1):
.
Подставим y
и y’
в уравнение (1):
![]()
![]() ,
:
,
:![]() .
.
Уравнения
Бернулли
имеют следующий вид: ![]()
Принцип решения:
![]()
![]()
Если обозначить
![]() за Z(x),
то
за Z(x),
то ![]() .
Отсюда
.
Отсюда ![]() .
Подставим это выражение выше и получим:
.
Подставим это выражение выше и получим:
![]()
Получили дифференциальное линейное уравнение, принцип решения которого рассмотрен выше.
Пример: ![]() ,
,
![]() ,
,
![]()
