1. Определение числовой функции. Способы задания функций. Числовой функцией одного переменного у=f(х) называют правило f , которое каждому значению переменной х из множества Х ставит в соответствие единственное значение переменной у из множества У.

Множество Х – область определения функции, множество У – область ее значений.Функция задана, если указано правило f.

Существуют три способа задания функции: аналитический, табличный и графический.

2. Понятие обратной функции.

Пусть задана некоторая функция у = f(х), которая каждому элементу из множества D (f) ставит в соответствие один элемент из множества Е ( f ). Если обратное соответствие есть тоже функция, то есть, каждому значению у E( f ) соответствует единственное значение х D ( f ), то ее называют обратной функцией по отношению к функции f (х).

3. Понятие сложной функции.

Если функция y зависит от переменной u, т. е. у = f (u), u U, а u, в свою очередь, является какой - либо функцией от независимой переменной х, т. е u = g (x), х Х, то переменная у называется функцией от функции (или сложной функцией) от x и записывается в виде Y = f (u), u = g (x), или y = f [g (x)].

Понятие сложной функции Пусть функция z = f(x,y) определена в некоторой окрестности точки (x0, y0) . Пусть ее аргументы x и y в свою очередь являются функциями x = x(t) , y = y(t) и определены в некоторой окрестности точки t0 , причем x(t0) = x0 , y(t0) = y0 .

Тогда в окрестности точки t0 определена сложная функция аргумента t z = f(x(t), y(t)). Аналогично определяется сложные функции любого числа переменных.

Например, если x и y — функции 2–х переменных: x = x(u,v) и y = y(u,v) , то функция z = f(x,y) является сложной функцией двух переменных u и v :

4. Числовые последовательности.

Последовательностью называется множество чисел, перенумерованных с помощью натуральных чисел и расставленных в порядке возрастания их номеров x1,x2,...xn

Числа x1,x2,...,xn — называются элементами последовательности, символ xn — общим элементом, а число n — его номером. Сокращенно последовательность обозначается символом {xn}. Счетным множеством называется множество эквивалентное множеству натуральных чисел. Следовательно любая последовательность является счетным множеством. 5.Определение предела последовательности.

Окрестностью точки x0 называется любой интервал, содержащий эту точку.δ — окрестностью точки x0 Uδ (x0) называется интервал длиной 2δ с центром в этой точке.

Число а называется пределом последовательности {xn}, если для любого ε > 0 найдется номер n0 = n0(ε) ∈ N такой, что для всех номеров n > n0 выполняется неравенство |xn — a| <ε

Число b называется пределом последовательности {xn}=x1, x2,..., xn (lim {xn} = b; n→∞)

Последовательность {xn}, имеющая конечный предел а, называется сходящейся.Последовательность, имеющая бесконечный предел или вообще не имеющая предела, называется расходящейся 6. Свойства пределов числовых последовательностей. Оператор взятия предела числовой последовательности является линейным, т. е. проявляет два свойства линейных отображений. 1)Аддитивность. Предел суммы числовых последовательностей есть сумма их пределов, если каждый из них существует. 2)Однородность. Константу можно выносить из-под знака предела. 3) Предел произведения числовых последовательностей факторизуется на произведение пределов, если каждый из них существует. 4)Предел часного числовых последовательностей есть отношение их пределов, если эти пределы существуют и последовательность-делитель не является бесконечно малой.

Свойства сохранения порядка

1)Если все элементы сходящейся последовательности, начиная с некоторого номера, не превышают некоторого числа, то и предел этой последовательности также не превышает этого числа. 2)Если некоторое число не превышает все элементы сходящейся последовательности, начиная с некоторого номера, то оно также не превышает и предела этой последовательности. 3)Если некоторое число строго превышает все элементы сходящейся последовательности, начиная с некоторого номера, то предел этой последовательности не превышает этого числа. 4)Если все элементы сходящейся последовательности, начиная с некоторого номера, строго превышают некоторое число, то это число не превышает предела этой последовательности. 5)Если, начиная с некоторого номера, все элементы одной сходящейся последовательности не превышают соответствующих элементов другой сходящейся последовательности, то и предел первой последовательности не превышает предела второй. Другие свойства 1)Сходящаяся числовая последовательность имеет только один предел. 2)Замкнутость. Если все элементы сходящейся числовой последовательности лежат на некотором отрезке, то на этом же отрезке лежит и её предел. 3)Предел последовательности из одного и того же числа равен этому числу. 4)Замена или удаление конечного числа элементов в сходящейся числовой последовательности не влияет на её предел. 5)У возрастающей ограниченной сверху последовательности есть предел. То же верно для убывающей ограниченной снизу последовательности. 6)Если у последовательности чисел существует предел , и если задана функция , определенная для каждого и непрерывная в точке , то

8. Определение ограниченной последовательности. Последовательность {xn} называется ограниченной снизу (сверху), если существует такое число C, что все члены последовательности удовлетворяют условию xn ≥ C (xn ≤ C). Последовательность, ограниченную как сверху, так и снизу, называют ограниченной.

Геометрически ограниченность последовательности означает, что все ее значения лежат на некотором отрезке. 9. Определение бесконечно малой последовательности. Последовательность {αn} называется бесконечно малой, если 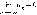Если число a – предел последовательности {xn}, то последовательность {αn}, где αn = xn – a, бесконечно малая. Примером бесконечно малой последовательности является геометрическая прогрессия {qn}, где|q|<1. 10. Свойства бесконечно малых последовательностей. Свойство 1. Произведение бесконечно малой последовательности и ограниченной последовательности есть бесконечно малая последовательность Следствие. Умножиение бесконечно малой последовательности на любое число дает бесконечно малую последовательность. Свойство 2. Сумма любого конечного числа бесконечно малых величин есть величина бесконечно малая. 11. Определение бесконечно большой последовательности. Последовательность {xn} называется бесконечно большой, если

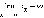
Другими словами, , если для любого δ > 0 найдется номер такой, что для любого Аналогично вводятся понятия бесконечных пределов +∞ и –∞. Примерами бесконечно больших последовательностей могут служить {n2} или {1 – n}.

13. Определение монотонных последовательностей. — это последовательность, элементы которой с увеличением номера не убывают, или, наоборот, не возрастают. Подобные последовательности часто встречаются при исследованиях и имеют ряд отличительных особенностей и дополнительных свойств. Последовательность из одного числа не может считаться возрастающей или убывающей. 14. Определение предела функции в точке. — такая величина, к которой стремится рассматриваемая функция при стремлении её аргумента к данной точке. Определение: Число b называется пределом функции y=f(x) при х → а, если, по мере того как x, приближается к а – будь то справа или слева значение f(x) неограниченно приближается к b.

15. Свойства пределов функций. Основные свойства предела функции в точке I. Если функция имеет предел при х → а, то только один. II. Если функция имеет предел при х → а, то она ограничена в некоторой окрестности точки a. III. Если существует и С-постоянная функция (число), то IV. Пусть , тогда: Если условия этих теорем не выполняются, то могут возникнуть неопределенности вида и др., которые в простейших случаях раскрываются с помощью алгебраических преобразований. 16. Правила вычисления пределов функций. Часть I. Основные способы вычисления пределов, содержащих неопределенности типа . Алгоритм решения. 1)Подставить в выражение предельное значение аргумента. 2)Определить есть или нет неопределенность. Если нет, дать ответ. 3)Если неопределенность есть, то по ее виду выбрать одно из правил устранения этой неопределенности 4)Преобразовать выражение согласно выбранному правилу, и к новой форме предела применить данный алгоритм, начиная с п.1. Правило 1. В числителе и знаменателе вынести x в максимальной степени, если это возможно. Заметим, что , а , где c - любое число. Правило 2. Числитель и знаменатель разделить одновременно на , если это возможно. Необходимо иметь в виду, что , а , где c - число, отличное от нуля.

Правило3. При вычислении пределов от иррациональных выражений, не попадающих в предыдущие правила, следует избавиться от корней, входящих в неопределенность. Возможны следующие способы: 1) замена переменной, позволяющая извлечь корни, входящие в неопределенность; 2) дополнение до формулы, позволяющей возвести корень в соответствующую ему степень; здесь используются формулы:  ; . Правило 4. При наличии неопределенности в пределе от выражения, содержащего тригонометрические функции, следует выделить в этом выражении первый замечательный предел: Можно использовать следствия этого предела: 1) 2) 3) 4) Правило 5. Вычисление предела сложнопоказательной функции Если рассматриваемый предел содержит неопределенность , то он сводится ко второму замечательному пределу: или Правило 6. Предел сложной функции: В частности, , если . Необходимо помнить свойства логарифмов : Есть пределы, которыми можно пользоваться как "табличными": ; ; 17. Определение бесконечно малой функции. Функция y=f(x) называется бесконечно малой при x→a или при x→∞, если или , т.е. бесконечно малая функция – это функция, предел которой в данной точке равен нулю. 18. Определение бесконечно большой функции. Функция называется бесконечно большой при , если .

19. Первый замечательный предел. Первым замечательным пределом называется предел

        Теорема Первый замечательный предел равен

20. Второй замечательный предел.   Вторым замечательным пределом называется предел

21. Определения односторонних пределов функции в точке. Односторо́нний преде́л в математическом анализе — предел числовой функции, подразумевающий «приближение» к предельной точке с одной стороны. Такие пределы называют соответственно левосторо́нним преде́лом (или преде́лом сле́ва) и правосторо́нним преде́лом (или преде́лом спра́ва). Пусть задана числовая функция и — предельная точка области определения M. 1)Число называется правосторонним пределом функции f при x стремящемся к a, если 2)Число называется левосторонним пределом функции f при x стремящемся к a, если