Поток векторного поля через поверхность. Определение дивергенции векторного поля и её свойства. Вычисление дивергенции в декартовых координатах.

Поток векторного поля через поверхность. Пусть в области D задано непрерывное векторное поле , . Возьмем в этом векторном поле некоторую поверхность S и выберем ее определенную сторону. Пусть – поле единичных нормалей к поверхности, соответствующее выбранной стороне. Тогда поверхностный интеграл 2-ого рода (т.к. ) называется потоком вектора A через поверхность S в указанную сторону.

П усть . Формула Гаусса-Остроградского:

Левую часть можно записать так: , , . Следовательно: , так как . Это поток вектора через замкнутую поверхность. Правую часть можно записать как дивергенцию (расходимость): .

Дивергенцией векторного поля A в точке MÎV называется производная функции по объему в этой точке: . Дивергенцию можно записать и с помощью оператора Набла: . Дивергенция в декартовых координатах: .

Свойства дивергенции:

• .

• .

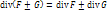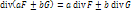Другие свойства (на лекции не разбирали, на усмотрение сдающего):

• Если u – скалярное поле, а F – векторное: .

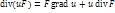• Свойство, связывающее векторные поля F и G, заданные в трёхмерном пространстве, с ротором: .

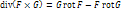• Дивергенция от ротора равна нулю: .

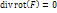Соленоидальные векторные поля, условия соленоидальности.

Пусть в некоторой области D задано непрерывное векторное поле (M)= (x,y,z). Потоком векторного поля через ориентированную кусочно-гладкую поверхность S, расположенную в области D, называется интеграл , где – единичный вектор нормали к поверхности S, указывающий на ее ориентацию, а – элемент площади поверхности S.

Векторное поле называется соленоидальным в области D, если поток этого поля через любую кусочно-гладкую несамопересекающуюся поверхность, расположенную в D и представляющую собой границу некоторой ограниченной подобласти области D, равен нулю.

Е сли дивергенция равна нулю, то есть , то поле вектора называется соленоидальным.

, поэтому поток везде, на каждом сечении трубки, одинаков.

Для того чтобы непрерывно дифференцируемое векторное поле было соленоидальным в объемно-односвязной области D, необходимо и достаточно, чтобы во всех точках D выполнялось равенство . Где дивергенцией (“расходимость”) векторного поля называется скалярная функция

Циркуляция векторного поля и ротор векторного поля. Вычисление ротора в декартовых координатах.

Циркуляцией векторного поля называется криволинейный интеграл второго рода, взятый по произвольному замкнутому контуру L:

Г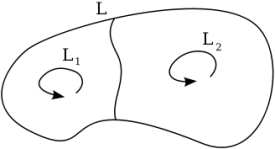 де — векторное поле (или вектор-функция), определенное в некоторой области D, содержащей в себе контур L, — бесконечно малое приращение радиус-вектора вдоль контура. Окружность на символе интеграла подчёркивает тот факт, что интегрирование производится по замкнутому контуру.

Циркуляция по контуру, ограничивающему несколько смежных поверхностей, равна сумме циркуляций по контурам, ограничивающим каждую поверхность в отдельности, то есть

– формула Стокса в векторном виде.

Вихревым вектором (вихрем) или ротором векторного поля называется вектор, имеющий координаты:

Ротор в декартовых координатах:

Если , то векторное поле называется безвихревым или потенциальном.

36. Оператор Гамильтона (набла), дифференциальные операции второго порядка, связь между ними.

Оператор набла (оператор Гамильтона) – векторный дифференциальный оператор, обозначаемый символом . Для трёхмерного евклидова пространства в прямоугольных декартовых координатах оператор набла определяется следующим образом: