
- •10) Геометрические приложения определённого интеграла: площади плоских фигур, длина кривых. Вычисление объёма тел, в том числе тел вращения.
- •11) Числовые ряды. Критерий Коши сходимости числового ряда. Следствие: необходимое условие сходимости ряда.
- •19. (Формула Коши-Адамара),
- •2 5. Определение двойного интеграла и его основные свойства.
- •Сведение двойного интеграла к повторному.
- •26. Тройной интеграл, сведение его к повторному.
- •27, Замена переменных в двойном интеграле. Пример: случай полярных координат.
- •28. Замена переменных в тройном интеграле. Примеры: случаи цилиндрических и сферических координат.
- •29. Вычисление площади гладкой поверхности, заданной параметрически и в явном виде. Элемент площади поверхности.
- •30. О пределение криволинейного интеграла первого рода, его основные свойства и вычисление.
- •Определение криволинейного интеграла второго рода, его основные свойства и вычисление. Связь с интегралом первого рода.
- •31. Формула Грина. Условия того, что криволинейный интеграл на плоскости не зависит от пути интегрирования.
- •32. О пределение поверхностного интеграла первого рода, его основные свойства и вычисление.
- •33. Теорема Гаусса-Остроградского, её запись в координатной и векторной (инвариантной) формах.
- •34. Теорема Стокса, её запись в координатной и векторной (инвариантной) формах.
- •35. Скалярное поле. Градиент скалярного поля и его свойства. Вычисление градиента в декартовых координатах.
- •Поток векторного поля через поверхность. Определение дивергенции векторного поля и её свойства. Вычисление дивергенции в декартовых координатах.
- •Соленоидальные векторные поля, условия соленоидальности.
- •Циркуляция векторного поля и ротор векторного поля. Вычисление ротора в декартовых координатах.
- •36. Оператор Гамильтона (набла), дифференциальные операции второго порядка, связь между ними.
- •37. Основные понятия, относящиеся к оду первого порядка: общее и частное решения, общий интеграл, интегральные кривые. Задача Коши, её геометрический смысл.
- •38. Интегрирование оду первого порядка с разделяющимися переменными и однородных.
- •39. Интегрирование линейных оду первого порядка и уравнений Бернулли.
- •40. Интегрирование оду первого порядка в полных дифференциалах. Интегрирующий множитель.
33. Теорема Гаусса-Остроградского, её запись в координатной и векторной (инвариантной) формах.
В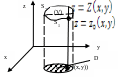 координатной форме.
Рассмотрим тело (V)
в пространстве с ограничивающей
поверхностью (S).
координатной форме.
Рассмотрим тело (V)
в пространстве с ограничивающей
поверхностью (S).
Рассмотрим некую
функцию R(x,y,z),
заданную в области (V)
и на границе, непрерывную в этой области
и на границе вместе со своими частными
производными первого порядка. Рассмотрим
интеграл ![]() .
Спроецируем тело на область D.
Возьмём точку (x,y).
.
Спроецируем тело на область D.
Возьмём точку (x,y).
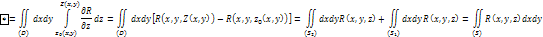
С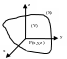 делаем
то же самое, но с проекцией на оси y
и z.
делаем
то же самое, но с проекцией на оси y
и z.
![]()
Теперь спроектируем на оси x и z.
![]()
Складывая эти формулы, получаем формулу Остроградского-Гаусса: . Формула сводит интеграл от объёма к интегралу по границе.
Если ![]() и
и ![]() или
или ![]() и
и ![]() или
или ![]() и
и ![]() ,
тогда
,
тогда ![]() .
А если
,
и
,
то:
.
А если
,
и
,
то: ![]() .
.
В общем виде теорема звучит так. Пусть в замкнутой ограниченной области (V) заданы функции P(x,y,z), Q(x,y,z) и R(x,y,z), непрерывные на (V) вместе со своими частными производными первого порядка. Тогда имеет место следующее тождество: .
З апись
формулы в векторном виде.
Пусть
апись
формулы в векторном виде.
Пусть ![]() .
В обычном виде формула выглядит так:
.
В обычном виде формула выглядит так:
![]()
Левую часть можно
записать так: ![]() ,
,
![]() ,
,
![]() .
Следовательно:
.
Следовательно: ![]() ,
так как
,
так как ![]() .
Мы получили поток
вектора через замкнутую поверхность.
Правую часть можно записать как
дивергенцию
(расходимость):
.
Мы получили поток
вектора через замкнутую поверхность.
Правую часть можно записать как
дивергенцию
(расходимость):
![]() .
В итоге формула
Гаусса-Остроградского в векторном виде:
.
В итоге формула
Гаусса-Остроградского в векторном виде:
![]() .
Читается так: поток вектора через
замкнутую поверхность равен интегралу
по объёму от его дивергенции.
.
Читается так: поток вектора через
замкнутую поверхность равен интегралу
по объёму от его дивергенции.
Дивергенцией
векторного поля A
в точке MÎV
называется производная функции ![]() по объему в этой точке:
по объему в этой точке: ![]() .
.
34. Теорема Стокса, её запись в координатной и векторной (инвариантной) формах.
![]() .
.
![]() {ф. Грина}=
{ф. Грина}=
=
![]() .
Аналогично
.
Аналогично
![]() c
c![]() ,
,
![]() c
c![]() .
.
Теорема: Пусть в некоторой окрестности поверхности S функции Р(х, у, z), Q(x, у, z) и R(x, у, z) непрерывны и имеют непрерывные частные, производные первого порядка. Тогда имеет место следующее соотношение:
![]() .
(Формула Стокса).
.
(Формула Стокса).
![]() .
.
Инвариантная
запись формулы Стокса:
Используя выражение для ![]() в ортогональном базисе
в ортогональном базисе ![]() ,
,
![]() :
:
![]() .
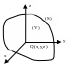
Укажем на поверхности S
определенную сторону, т.е. укажем
непрерывное поле единичных нормалей
.
Укажем на поверхности S
определенную сторону, т.е. укажем
непрерывное поле единичных нормалей
![]() .
Используя стандартное обозначение
cosx,
cosy, cos
.
Используя стандартное обозначение
cosx,
cosy, cos![]() для координат единичного вектора
нормали
к поверхности S
получим:
для координат единичного вектора
нормали
к поверхности S
получим: ![]() .
Из соотношения видно, левая часть формулы
Стокса может быть записана в виде
.
Из соотношения видно, левая часть формулы
Стокса может быть записана в виде ![]() .
Скалярное произведение:
.
Скалярное произведение: ![]() и элемент площади
и элемент площади ![]() поверхности S не зависят от выбора
декартовой прямоугольной системы
координат в пространстве, и при переходе
к новому ортогональному базису
поверхности S не зависят от выбора
декартовой прямоугольной системы
координат в пространстве, и при переходе
к новому ортогональному базису ![]() ',
', ![]() левая часть формулы не изменит своего
значения и формы – инвариантна.
левая часть формулы не изменит своего
значения и формы – инвариантна.
Рассмотрим
![]() .
Пусть
.
Пусть ![]() – единичный вектор касательной в точках
границы L поверхности S, cosa, cosb, cos
– единичный вектор касательной в точках
границы L поверхности S, cosa, cosb, cos![]() – координаты этого вектора.
– координаты этого вектора. ![]() ,
,
![]() .
Т.о
.
Т.о![]() –
циркуляция векторного поля p
по кривой L.
–
циркуляция векторного поля p
по кривой L.
![]() -
инвариант.
Получаем
-
инвариант.
Получаем
![]() =
=![]() .
.
Условия того, что криволинейный интеграл в пространстве не зависит от пути интегрирования.
Следствие из
теоремы Стокса:
Необходимым условием того, что
криволинейный интеграл ![]() не зависит от пути интегрирования,
является условие:
не зависит от пути интегрирования,
является условие: ![]() ,
,
![]() ,
,
35. Скалярное поле. Градиент скалярного поля и его свойства. Вычисление градиента в декартовых координатах.
Пусть D – область на плоскости или в пространстве. Говорят, что в D задано скалярное поле, если каждой точке области D ставится в соответствие некая функция U(M).
Определение
по-другому. Скалярное поле определяется
скалярной функцией точки ![]() ,
где M(x,y,z)
– точка пространства,
,
где M(x,y,z)
– точка пространства, ![]() – её
радиус-вектор.
– её
радиус-вектор.
Определение
градиента.
Градиентом скалярной функции u(M),
определенной и дифф в некоторой области
D,
называется вектор ![]() .
.
![]() .
Знак
.
Знак ![]() - это вектор
Набла.
- это вектор
Набла. ![]()
![]() (
(![]() – единичный вектор с координатами:
– единичный вектор с координатами:
![]() ).
).
Из последнего
выражения видно, что ![]() максимально, когда
совпадает с направлением градиента.
Следовательно, градиент показывает
направление наибольшего изменения
скорости функции.
максимально, когда
совпадает с направлением градиента.
Следовательно, градиент показывает
направление наибольшего изменения
скорости функции.
Градиент скалярного поля – вектор.
Свойства градиента:
Определение векторного поля. Поле градиента. Потенциальные поля, условия потенциальности.
Векторное поле.
Если каждой точке М
некоторой области V
пространства
соответствует значение некоторой
векторной величины ![]() (M),
то говорят, что в области V
задано
векторное поле
(M).
Примеры векторных полей – поле тяготения,
поля электрической и магнитной
напряжённостей, поле скоростей частиц
движущейся жидкости.
(M),
то говорят, что в области V
задано
векторное поле
(M).
Примеры векторных полей – поле тяготения,
поля электрической и магнитной
напряжённостей, поле скоростей частиц
движущейся жидкости.
Если в некоторой
декартовой системе координат вектор
(M)
имеет координаты Р(M),
Q(M),
R(M),
то ![]() .
Таким образом, задание векторного поля
(M)
эквивалентно заданию трёх скалярных
полей Р(M),
Q(M),
R(M).
Будем называть векторное поле гладким,
если его координатные функции - гладкие
скалярные поля.
.
Таким образом, задание векторного поля
(M)
эквивалентно заданию трёх скалярных
полей Р(M),
Q(M),
R(M).
Будем называть векторное поле гладким,
если его координатные функции - гладкие
скалярные поля.
Градиентом
дифференцируемого скалярного поля
u(M)=u(x,y,z) называется вектор ![]() .
Т.е. сумма частных производных умноженных
на соответствующие единичные вектора.
.
Т.е. сумма частных производных умноженных
на соответствующие единичные вектора.
В общем случае градиент вводится как векторная характеристика скалярного поля — то есть области, каждой точке которой соответствует значение определенного скаляра. Градиент характеризует, насколько быстро меняется скалярная величина в том или ином месте этого поля.
Потенциальные
векторные поля. Векторное
поле A = {Ax, Ay, Az} называется потенциальным,
если вектор А является градиентом
некоторой скалярной функции u = u(x, y,
z): A
= grad
u
= ![]() (16.7).
(16.7).
При этом функция u называется потенциалом данного векторного поля.
Выясним, при каких
условиях векторное поле является
потенциальным.
Так как из (16.7) следует, что ![]() ,
То
,
То ![]() ,
,![]() =
=![]() ,
,
![]() =
=![]() .
так как смешанная производная второго
порядка не зависит от порядка
дифференцирования. Из этих равенств
легко получаем, что rot A = 0 -условие
потенциальности векторного поля.
.
так как смешанная производная второго
порядка не зависит от порядка
дифференцирования. Из этих равенств
легко получаем, что rot A = 0 -условие
потенциальности векторного поля.
Ротором векторного
поля
(M)
в точке ![]() называется векторная величина (векторное
поле):
называется векторная величина (векторное
поле): ![]() .
Если выразить
.
Если выразить ![]() через оператор Гамильтона набла:
равен векторному произведению
через оператор Гамильтона набла:
равен векторному произведению ![]() .
Действительно,
.
Действительно, ![]() .
.
