27, Замена переменных в двойном интеграле. Пример: случай полярных координат.

Замена переменных в произвольном двойном интеграле.

Вычислим интеграл , используя замену переменных . Рассмотрим интеграл как предел интегральных сумм. Область (D) сеткой кривых разделяется на частичные области D_i, внутри каждой частичной области берём произвольные точки (x_i, y_i). Составляем интегральную сумму: , где D_i – площадь i-ой частичной области. Устремим максимальный диаметр к нулю: . По определению, . Совершим замену переменных (*). При замене (*) площадь .

Если , то и , следовательно,

– якобиан преобразования (*).

П ример с полярными координатами.

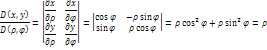
1. 28. Замена переменных в тройном интеграле. Примеры: случаи цилиндрических и сферических координат.

Замена переменных в тройном интеграле в общем случае.

П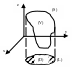 усть имеется тело (V) с границей (S).

Пусть , тогда .

Замена:

П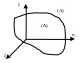 реобразование (*) будем считать взаимно-однозначным, то есть всё можно выразить друг через друга, а именно:

Пусть поверхность (Λ) задаётся параметрически, то есть:

Получаем параметрическое задание поверхности (S) (см. рис. ниже).

Два последних двойных интеграла равны, так как: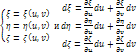

Применим к последнему выражению формулу Гаусса-Остроградского, то есть эту формулу: .

Пусть , , , тогда:

Выражение в скобках равно нулю. Оставшееся выражение запишем так:

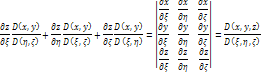
Это якобиан преобразования. Окончательно получаем:

А для общего случая:

Ц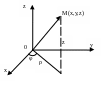 илиндрические координаты:

Переходим от координаты M(x,y,z) к M(ρ,φ,z). Это цилиндрические координаты, где:

Получаем, что .

С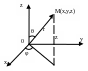 ферические координаты:

Получаем элемент объёма сферических координат: .

29. Вычисление площади гладкой поверхности, заданной параметрически и в явном виде. Элемент площади поверхности.

Р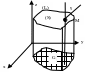 ассмотрим кусок поверхности S, заданной уравнением F=(x,y,z)=0. Пусть выполняется условие , что означает, что в каждой точке поверхности существует нормаль с направляющим вектором . Разобьем поверхность S сеткой гладких кривых на элементарные области (разбиение Z). Пусть   – наибольший из диаметров элементарных областей. Если независимо от разбиения Z существует , то он и называется площадью данной поверхности. Пусть S однозначно проектируется на плоскость xy и  G – это проекция. Элементу площади dxdy области G на плоскости xy соответствует элемент площади поверхности S, равный , где – угол между нормалью к поверхности S и осью Z. Поэтому вычисление площади поверхности сводится к вычислению двойного интеграла  по проекции поверхности на плоскость. Если поверхность задана уравнением , , а нормаль представляет собой градиент функции, то есть: , то     и площадь поверхности вычисляется по формуле:

, здесь G – проекция поверхности S на плоскость xy.

Если поверхность однозначно проектируется на другие координатные плоскости, то соответственно изменится формула вычисления площади поверхности.

Если кривая задана параметрическими уравнениями и , то площадь криволинейной трапеции, ограниченной этой кривой, прямыми и и отрезком [a,b] оси Ox, выражается формулой где определяются из уравнений

Площадь криволинейного сектора, ограниченного кривой, заданной в полярных координатах уравнением и двумя полярными радиусами  находится по формуле

.