19. (Формула Коши-Адамара),

Радиусом сходимости ряда  наз такое число R, что для всех х, |х|<R, степенной ряд абсолютно сходится, я для всех х, |х|>R – расходится. Интервал ]-R;R[ наз интервалом схобимости.

ассмотрим функцию . Ее областью определения является множество тех значений x, при которых ряд сходится. Область определения такой функции называется интервалом сходимости. Если интервал сходимости представляется в виде , где R > 0, то величина R называется радиусом сходимости. Сходимость ряда в конечных точках интервала проверяется отдельно. Радиус сходимости можно вычислить, воспользовавшись радикальным признаком Коши, по формуле

или на основе признака Даламбера:

20) Разложение функций в степенные ряды. Ряд Тейлора. Достаточное условие Разложимости функций в ряд Тейлора.

опр.: Пусть  . Тогда ряд   наз-ся рядом Тейлора ф-ии   в точке  . Если  , то   по ф-ле Тейлора:  , где   - остаточный член ф-лы Тейлора, т.е.  , где   - n-ая частичная сумма ряда Тейлора ф-ии   в точке  . ряд Тейлора сходится на  тогда и только тогда, когда    . теор.: Пусть   и        , тогда на     док-во:  , где   - остаточный член формулы Тейлора в форме Лагранжа        . Рассм. ряд  ,   по признаку Даламбера ряд сх-ся  . Перейдем к пределеу при   в неравенстве 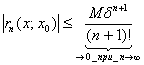       на  .

20) Основные разложения элементарных функций в ряд Тейлора

2 5. Определение двойного интеграла и его основные свойства.

О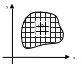 пределение двойного интеграла. Пусть на плоскости XY задана функция и область (P) (область задания функции f(x,y)), её площадь P. Произведём разбиение площади сеткой кривых P_i, где P_i – частичная область. Внутри частичной области возьмём произвольную точку с координатами (ξ_i,η_i). Составим интегральную сумму: . Пусть λ – характеристика разбиения, которая равна , где d_i – диаметр частичной области. Диаметр – максимальное расстояние между любой парой точек в области. Устремим λ к нулю. Если существует предел интегральных сумм , то этот предел и называется двойным интегралом: .

Основные свойства двойного интеграла:

• Свойство аддитивности:

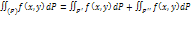
• Свойства линейности:

а)

б)

• Модуль интеграла меньше или равен интегралу от модуля:

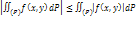
• Теорема о среднем. Так как 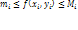, то, проинтегрировав это неравенство, получим:

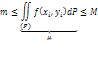
, где .

Сведение двойного интеграла к повторному.

Т еорема. Если функция f(x, y) интегрируема в прямоугольнике, указанном на рисунке, и если  и существует интеграл , тогда существует повторный интеграл  и он равен двойному:  = .

З амечание. Если f(x, y) интегрируема в прямоугольнике, указанном на рисунке, и  и существует интеграл  тогда существует повторный интеграл .

Предположим, что область D произвольного вида. Делаем разбиение и проводим параллельные линии. Заключим область (D) в прямоугольник (D^*), , и в нём определим функцию f^*(x,y): .

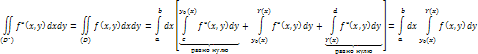
Формула в общем виде: . Так же доказывается, что .

26. Тройной интеграл, сведение его к повторному.

О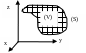 пределение тройного интеграла. Пусть в некоторой области (V) с границей (S) задана в каждой точке функция f(x,y,z). Разобьём тело (V) сеткой поверхностей на частичные области (V_i). В каждой (V_i) возьмём произвольную точку (ξ_i, η_i, ζ_i) и составим интегральную сумму: . Устремим максимальный диаметр (макс. расстояние между любой парой точек в области) к нулю: . Тогда, если существует предел интегральных сумм, то он равен тройному интегралу: .

На всякий случай определение интегральной суммы. Пусть на нек-ом отрезке задана . Произведём разбиение отрезка: . Число , называется интегральной суммой функции f(x), соответствующей данному разбиению T(ξ_i;x_i) сегмента [a;b] и данному выбору промежуточных точек ξ_i на частичных сегментах [x_i-1;x_i], Δ –хар-тика разбиения:

С ведение к повторному интегралу. Рассмотрим первый простейший случай. Пусть тело V – прямоугольный параллелепипед. Проведём секущую плоскость. Возьмём приращение плоскости (жирные линии). Тогда: .

Р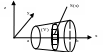 ассмотрим второй случай.

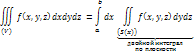
Рассмотрим третий случай – область (V) цилиндрического типа.