
- •«Введение в математический анализ»
- •1) Опр. Числовой последовательностью называется отображение множества натуральных чисел n во множество
- •Основные характеристики числовых последовательностей:
- •4) Опр. Функцией или отображением множества X во множество y, называется правило f по которому, каждому элементу X множества X поставлен в соответствие единственный элемент y множества y.
- •Способы задания функции:
- •5) Функция называется явно заданной, если она задана формулой , в которой правая часть не содержит зависимой переменной. Пример: .
- •Свойства бесконечно малых функций:
- •Алгоритм устранения неопределенности основных функций:
- •15) Опр. Функция называется непрерывной в точке , если она определена в этой точке и ее значение равно пределу функции в этой точке:
- •Свойства функции непрерывности в точке:
Свойства бесконечно малых функций:
-
Алгебраическая сумма бесконечно малых
при
 функций, является бесконечно малой
функцией.
функций, является бесконечно малой
функцией.
- Произведение конечного числа бесконечно малых при функций, является бесконечно малой функцией.
-
Произведение бесконечно малой при
функции и ограниченной в некоторой
окрестности точки
 функции является бесконечно малой
функцией.
функции является бесконечно малой
функцией.
Теорема:
Если функция
при
имеет предел равный а,
то ее можно представить в виде суммы
числа а
и некоторой бесконечно малой при
функции
 ,
то
,
то
 .
.
11)
Функция
называется бесконечно
большой функцией
при
, если
для
любого
положительного
числа
существует такое положительное число
 ,
что для всех
неравных
и удовлетворяющих условию
,
что для всех
неравных
и удовлетворяющих условию ,
выполняется неравенство
,
выполняется неравенство
 .
Функция
y=f(x) называется бесконечно
большой функцией
при
,
если
для
любого
положительного
числа
существует такое положительное лицо
.
Функция
y=f(x) называется бесконечно
большой функцией
при
,
если
для
любого
положительного
числа
существует такое положительное лицо
 ,
что для всех х удовлетворяющих условию
,
что для всех х удовлетворяющих условию
 ,
выполняется неравенство
,
выполняется неравенство
Если
, есть бесконечно малая при
(
)
функция,
то
функция
 будет
бесконечно
большой
при
(
)
функцией
(и
обратно).
будет
бесконечно
большой
при
(
)
функцией
(и
обратно).
Опр.
Функция
называется бесконечно
малой функцией
при
,
если для любого положительного числа
существует такое положительное число
,
что для всех
и удовлетворяющих условию
выполняется неравенство

Опр.
Функция
называется бесконечно
большой функцией
при
,
если для любого положительного числа
существует такое положительное число
,
что для всех
удовлетворяющих условию
 выполняется неравенство
выполняется неравенство


Теорема:
Если
есть бесконечно малая при
 ,
то функция
,
то функция
 будет бесконечно большой при
функцией.
будет бесконечно большой при
функцией.
Обр. утв. Если функция бесконечно большая при , то будет бесконечно большой при функцией.
12) ,
,
 ,
, ,
, ,
, ,
, и др.
и др.
Алгоритм устранения неопределенности основных функций:
 ,
где
,
где
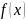 и
и
 – целые рациональные функции и
– целые рациональные функции и
 .
В этом случае, имеем неопределенность
вида
.
Для ее раскрытия разлагаем
числитель и знаменатель дроби.
.
В этом случае, имеем неопределенность
вида
.
Для ее раскрытия разлагаем
числитель и знаменатель дроби.
, где и – рациональные функции. В этом случае, имеем неопределенность вида . Для ее раскрытия выносим за скобку в числителе и знаменателе дроби x с наибольшим показателем, среди всех слагаемых дроби.
, где или – иррациональная функция и . В этом случае, имеем неопределенность вида . Для ее раскрытия умножаем числитель и знаменатель дроби на одно и то же выражение, приводящее к формулам сокращенного умножения. В случае квадратного корня, на сопряженное иррациональное выражение, приводящее к разности квадратов.
13)
Опр.
Первым
замечательным пределом
называется
 ,
применяется при раскрытии неопределенности
вида
от выражений содержащих тригонометрические
или обратные тригонометрические
функции;
,
применяется при раскрытии неопределенности
вида
от выражений содержащих тригонометрические
или обратные тригонометрические
функции;
вторым
замечательным пределом называется
 ,
применяется для раскрытия неопределенности
вида
,
применяется для раскрытия неопределенности
вида
 от выражений содержащих степенно-показательную
функцию.
от выражений содержащих степенно-показательную
функцию.
14)
Рассмотрим две бесконечно малые при
 функции
функции
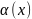 и
и
 ,
если
,
если
 ,
где
,
где
 ,
то функции
и
,
называются бесконечно малыми функциями
одного порядка при
.
,
то функции
и
,
называются бесконечно малыми функциями
одного порядка при
.
Если
 ,
то функция
называется бесконечно малой более
высокого порядка, по сравнению с функцией
при
.
,
то функция
называется бесконечно малой более
высокого порядка, по сравнению с функцией
при
.
Если
 ,
то функция
называется бесконечно малой более
высокого порядка, по сравнению с функцией
при
.
,
то функция
называется бесконечно малой более
высокого порядка, по сравнению с функцией
при
.
Опр.
Бесконечно малые при
функции
и
,
называются эквивалентными,
бесконечно малыми при
,
если
 .
.
Если
бесконечно малая при
функция, то верны следующие эквивалентности:



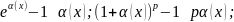
Теорема: Предел отношения двух бесконечно малых функций не измениться, если каждую или одну из них заменить эквивалентной ей бесконечно малой функцией.
