26.Понятие несобственных интегралов II рода. Пример интеграл Дирихле II рода.

НИ2-это опр инт-л от ф-ии, имеющей разрыв 2-го рода на конечн отр-ке инт-ия. Если т-ка разрыва 2-го рода совпала с левым концом инт-ия, то . Если т-ка раз-ва 2-го рода совпала с левой границей инт-ия(т. b), то если т. разрыва попала в к-ую-либо точку с, то

27.Понятие дифференциального уравнения I порядка, его общего и частного решения.

Ур-е вида f(x,y,y`)=0 наз-ют обыкновенным ДУ1. Общ реш ДУ1 наз-ся ф-ия , к-я зависит от одного произвол. постоянного С и удовлетв условиям: а)она удовл-т ДУ при любом конкр. знач. С. б) каково бы ни было нач усл-е y=Yo при x=Xo, можно найти такое знач с=Со, что ф-я y= удовл-ет данному нач усл-ю. частным реш наз-ся любая ф-ия y= , к-я получ-ся из общ реш-я y= , если в последнем произвол-му постоян-му С придать опред. знач с=Со.

28. Ду с разделяющимися переменными. Пример.

Уравнение вида: , а также вида: называются уравнениями с разделяющимися переменными.

Общие решения:

Пример:

29. Геометрическая интерпретация общего решения и решения задачи Коши.

Геометрический смысл задачи Коши состоит в определении той интегральной кривой, которая проходит через заданную точку

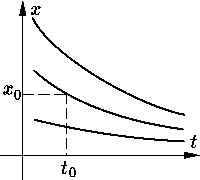
Однопараметрическое семейство функций , зависящих от параметра С из некоторой области и непрерывно дифференцируемых по х в некотором интервале (a,b), называется общим решением уравнения

, где f – заданная функция двух переменных, определенная в некоторой области , если:

1. Функция 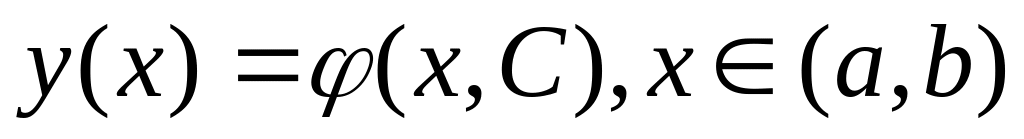, является решением данного уравнения для любого фиксированного С и из области .

2. Для любых начальных условий 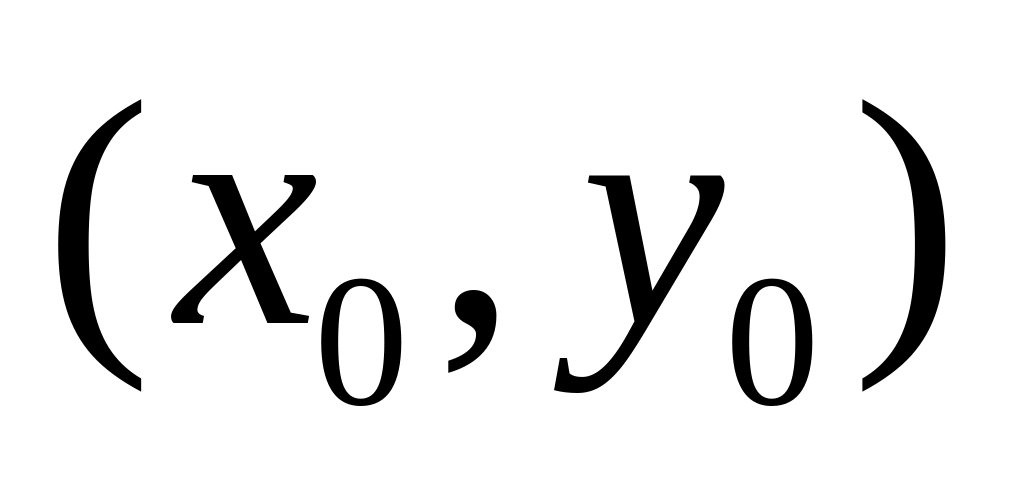из области D существует 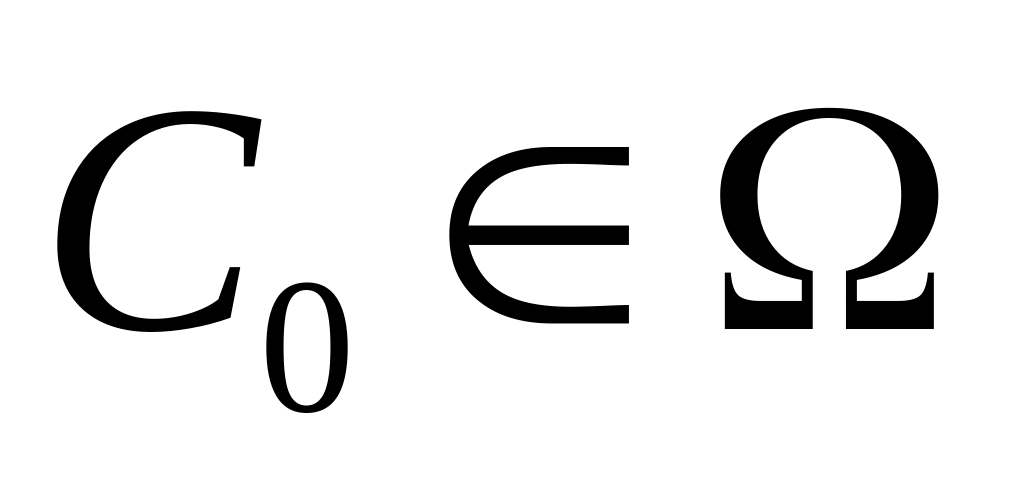такое, что .

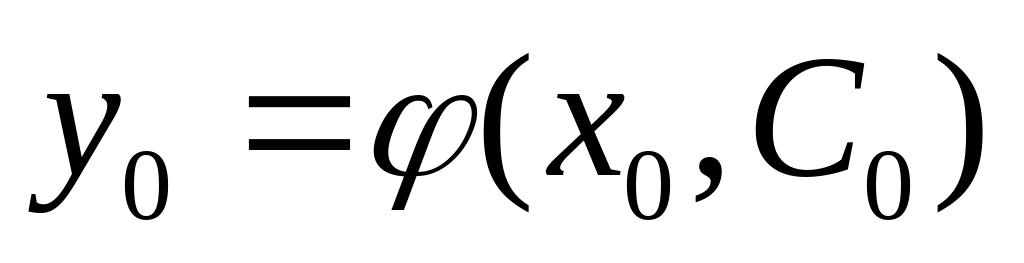30.Линейные дифференциальные уравнения I порядка и уравнения Бернулли.

_{Имеют вид: y’=f(x,y) (1) F(x,y,y’)=0 (2)}

_{1) y’=f(x) dy/dx=f(x)}

_dy=f(x)dx _dy=_{f(x)dx y=}_f(x)dx

_{2) y’=f(y) dy/dx=f(y)}

25. 

_{3) f(x)dx=f(y)dy ДУ с разделенными переменными} _f(x)dx=_f(y)dy

_{4)y’=f(x)gy или M(x)N(y)d(x)=K(x)L(y)d(y)}

_{ДУ с разделяющимися переменными}

_{Ур-е вида (4) реш по схеме:}

_{d(y)/d(x)=f(x)gy}

_{d(y)/g(x)=f(x)d(x)}

_{M(x)d(x)/K(x)=L(y)d(y)/N(y)}

25. 

_{5) y’=g(y/x) однородное ДУ 1го порядка (ф-ция вида f(αx,αy)=α}^k_g(x,y) наз однор ф-ция k-того порядка,αЄR)

реш с помощью подстановки

z=y/x y=zx y’=z’_xx+z

_{z’x+z=g(z) d(z)/(g(z)-z)=d(x)/x}

_{6) y’=f(ax+by) приводится к ур-ю вида (4) путем замены z=ax+by}

31.Структура общего решения линейного однородного дифференциального уравнения II порядка.

Обыкн ДУ 2 порядка с пост.коэфф. имеет вид:

(1) y``+py`+qy=r(x) p,q принадл. R, r(x) – функция

Если r(x) =0, то

(2) y``+ py`+qy=0 – однор.лин.ДУ с пост.коэфф.

Ур-е вида (3) =0 – характерист.ур-е (1) и(2) Стр-ра общего решения ур.(2) определяется корнями квадр.ур-я. (3)

Возможны 3 случая

1. кв.ур-е имеет разные корни α1 α2, D>0 тогда общее решение:

y=C1 C1, C2 прин.R

2. корни кв.ур. кратные, т.е. α1= α2=α ; D=0

y= C1, C2 прин.R

3. корни комплексно сопряженные : λ1= α-βi; λ2= α+βi;

y= C1 C1, C2 прин.R