8)Решение слау методом Крамера и матричным методом
На практике используют формулы крамера ,для решения систем уравнеий: Хi=Ai/|A| где (i= 1,2,…..n) эти формулы позволяют max неизвестные в виде дроби ,знаменателем которых явл. Определитель матрицы системы,а числитель определитель матрицы ai, получили из А заменой столбца коэффициентов, при вычисляемом неизвестном ,столбцов свободных членов.
Существует обратная матрица А-1. Умножив левую и правую части записи системы в матричной форме (А*Х=B) слева на А-1,,получен А-1(А*Х)=А-1B= (A-1*A)*X = A-1*B=E*X=A-1*B,а матрица умножается на единичную , получили X=A-1*B эта формула дает способ решения системы линейных уравнений,требующей отыскания , обратной матрицы и поэтому наз. Матричной.
9)Определение равносильных слау. Теорема равносильности слау
10.Определение вектора, единичного вектора, нулевого вектора, длины вектора. Формула для находжения координат и длины вектора
Вектор - это направленный отрезок.
Если длинна вектора равна 1, то вектор называется единичным.
Вектор у которого начало и конец совпадают называется нулевым.
Расстояние между началом и концом вектора называют его длинной (IABI)
формула для нахождения координат вектора (x2-x1, y2-y1, z2-z1)
Если вектор а имеет координаты (x,y,z),то его длина определяется по формуле: вектор |a|= корень квадратный из x в квадрате, плюс y в квадрате, плюс z в квадрате.
11.Определение суммы и разности вектора. Определение противоположных векторов. Операции над векторами в координатной форме
Суммой вектора а и вектор в, называется вектор а+в, который идёт из начла вектора а в конец вектора в, при условии что вектор в приложен к концу вектора а.
Два вектора называются противоположными если их сумма равна нулевому вектору. Вектор противоположный вектору а обозначают -а
Ненулевые противоположные векторы имеют равные длины и противоположные направления
Разностью вектора а и вектора в называют вектор а-в, который представляет собой сумму вектора а и противоположный вектор( -в)
а-в=а+(-в) (сверху поставить чёрточку-вектор)
Операции над векторами
а+в=(х1+х2;у1+у2;z1+z2)
а-в=(х1-х2;у1-у2;z1-z2)
a*£(число)= (х*£,у*£,z*£)
12.Определение коллинеарных векторов. Определение равных векторов. Теорема об условии коллинеарности двух векторов. Условие ортогональности двух векторов.Формула для нахождения угла между двумя векторами
Два вектора называются коллинеарными если они лежат на одной прямой или на параллельных прямых.
Эти
векторы могут быть направлены как
одинаково так и противоположно.
Векторы являются равными если они коллинеарны, сонаправлены и их длины равны.
Условия коллинеарности:
Если соотв. координаты векторов пропорциональны, то эти векторы коллиниарны,т.е.
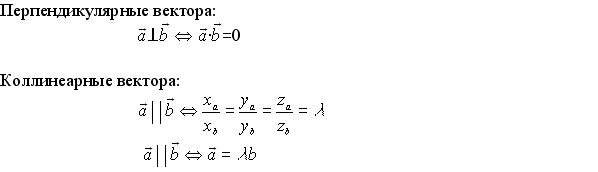
Условие ортогональности
Углом между двумя векторами, отложенными от одной точки, называется кратчайший угол, на который нужно повернуть один из векторов вокруг своего начала до положения сонаправленности с другим вектором.
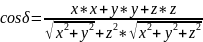
13.Вывести определение уравнения прямой , проходящей через одну точку, перпендикулярно данному вектору. Определение вектора нормали прямой.
Уравнение прямой, проходящей через данную точку перпендикулярно данному вектору.
Уравнение прямой L , проходящей через точку Мо (Хо; Уо) и перпендикулярной вектору n (А;В) имеет вид L А(Х-Хо) + В(У-Уо) = 0. Замечание: Не нулевой вектор перпендикулярный данной прямой называется вектором нормали прямой.