4. Абсолютные величины, их основные виды

Обобщающие показатели могут быть представлены абсолютными, относительными и средними величинами.

Абсолютные- это первичные обобщающие показатели характеризующие размеры общественных явлений в конкретных условиях места и времени.

По способу выражения размеров изучаемых явлений абсолютные величины делятся:

- индивидуальные обобщающие величины – они характеризуют размеры количественных признаков у отдельных единиц совокупности.

- суммарные – определяются на основании индивидуальных величин и могут быть выражены либо в виде численности ед. совокупности(число предприятий, число рабочих), либо в виде величин признака характеризующего данное общественное явление(объем продукции).

Абсолютные величины – числоименнованные, имеющие размерность.

Все абсолютные величины могут быть выражены:

1.натуральные ед. измерения (т.е. в физических мерах измерения)

2.условнонатуральные ед. измерения – пименяются для измерения объема однородной, но не одинаковой продукции.

3.стоимостные ед. измерения – в основе лежит цена, применяется для однородной и разнородной продукции, определяет товарную продукцию, валовую продукцию, реализованную продукцию, чистую продукцию, условно-чистую продукцию.

4.трудовой метод- это трудоемкость в трудозатраты, в чел/час, в чел/дни.

Относительные величины, их значения и основные виды

Относительные величины – это обобщающие показатели получаемые в результате сравнения 2-х стат. величин, где в числителе находится показатель отражается то явление которое изучается – сравниваемый показатель, а в знаменателе – показатель с которым производится сравнение – это показатель или база сравнения.

В зависимости от того, какое числовое значение имеет база сравнения, результат отношения может быть выражен:

1.в форме коэффициента – если база принята за единицу

2.в процентном – если база принята за 100%

3.в промилле – если база принята за 1000

4.в децимилли – если база принята за 10000

Условия применения баз сравнения:

1.если сравниваемый показатель больше базы – то применяются коэффициенты и проценты

2.если сравниваемый показатель незначительно меньше базы – то в процентах

3.если сравниваемый показатель значительно меньше базы – то в промилле и децимилли.

Обязательное условие применения относительных величин – показатели которые сравниваются должны быть сопоставимы во времени и пространстве, одинаковы по методологии сбора и обработке стат. информации.

Относительные величины могут быть представлены как соотношение:

I -одноименных показателей

1.относительная величина выполнения договорных обязательств = объем фактически выполненных обязательств / объем обязательств предусмотренных в договоре (100%)

2.относительная величина структуры = величина изучаемой части совокупности / величину все совокупности (100%)

3.относительные величины динамики – характеризуют изменения изучаемого явления вовремени выявляют направление развития измеряют интенсивность развития, могут быть выражены в виде темпов роста и других показателей динамики.

y_1, y_2, y₃

цепные T_2/1= T_3/2= базисные T_2/1 = T_3/1 =

4.относительная величина планового задания – это отношение величины показателя по плану к его фактической величине в предшествующем периоде.

5.относительная величина выполнения плана – это отношение фактической величины показателя к запланированной за тот же период его величине

6.относительная величина динамики – это произведение относительной величины планового задания на относительную величину выполнения плана.

7.относительная величина сравнения – характеризует количественное соотношение одноименных показателей относящихся к различным объектам стат. наблюдения

8.относительная величина координации – применяется для хар-ки соотношения между отдельными частями стат. совокупности и показывает во сколько раз сравниваемая часть совокупности больше или меньше части которая принимается за базу сравнения.

II – разноименные показатели – это относительные величины интенсивности. Показывают на сколько широко распространено изучаемое явление в той или иной среде, они числоименнованые, имеющие размерность.

Относительная величина интенсивности – это отношение абсолютной величины изучаемого явления к абсолютной величине характеризующей объем среды в которой происходит развитие или распространение явления.

К этим величинам относятся: показатели потребления продуктов питания на душу населения, различные соц. показатели, экономические показатели, фондоотдача, фондоемкость и т.д.

Сущность и значение средней величины

Средняя величина – это обобщающий показатель характеризующий типичный размер определенного признака у единиц качественно-однородной совокупности.

Статистические средние рассчитываются на основе массовых данных правильно организованного массового наблюдения; считается что стат. средняя будет объективна, если она рассчитывается по данным качественно-однородной совокупности. Если совокупность не однородна, то необходимо ее расчленить на группы из которых затем исчислить средние – в этом заключается связь метода средних и группировок.

Средняя величина – величина абстрактная, потому что характеризует значения абстрактной единицы, которой может и не быть в совокупности; величина именованная, имеющая размерность признака.

Виды средних величин и методы их расчета

Все средние величины выходят из одной степенной средней: , где

х – варианты осредняемого признака,

n – число вариантов,

m – показатель степени средней.

При: 1) m=1 - средняя арифметическая

2) m=0 - средняя геометрическая

3) m= -1 - средняя гармоническая

4) m=2 - средняя квадратическая

5) m=3 - средняя кубическая

Все виды средних могут быть исчислены по индивидуальным значениям осредняемого признака – называется простая или не взвешенная; по сгруппированным с указанием весов – взвешенная средняя. Разные виды средних при одних и тех же исходных данных имеют различные значения: чем выше показатель m, тем больше величина соответствующей средней. _гарм < _геом < _ариф < _{квадрат}

Правило Мажорантности – это свойство средних возрастать с повышением показателей степени определяющей функции.

Наиболее часто применяются средняя арифметическая (простая) (взвешенная), и средняя гармоническая (простая) 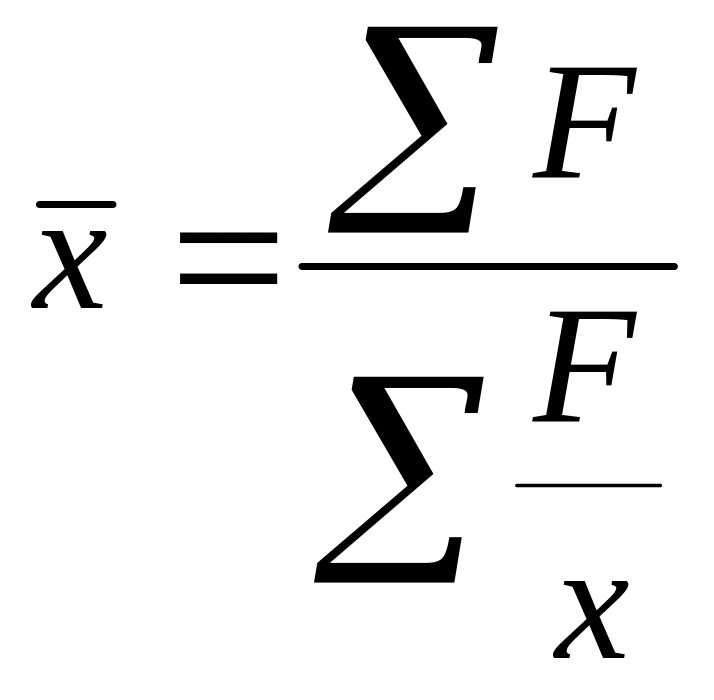(взвешенная).

Основные свойства средней арифметической

Средняя арифметическая обладает рядом математических свойств, которые имеют важное значение для упрощения расчетов средней ( )

- если все значения признака уменьшить (увеличить) на одно и тоже произвольное число, то новая средняя арифметическая будет меньше (больше) на то самое число ( )

- если все значения признака разделить (умножить), то новая средняя уменьшится (увеличится) во столько же раз ( )

- средняя арифметическая постоянной величины равна этой постоянной (если х=с то )

- если все частоты разделить или умножить на какое-либо произвольное число, то средняя от этого не измениться ( )

- произведение средней на сумму частот всегда равно сумме произведений вариант на частоты ( )

- сумма положительных и отрицательных отклонений индивидуальных значений признака от средней равна нулю ( ).

Упрощенный расчет средней арифметической – способ моментов, или способ отсчета от условного нуля

Свойства средней арифметической применяем для упрощения расчетов.

СПОСОБ ОТСЧЕТА ОТ УСЛОВНОГО НУЛЯ или СПОСОБ МОМЕНТОВ:

1. из всех значений признака вычесть произвольную постоянную величину – лучше значение серединной варианты или варианты имеющей наибольшую частоту.

2. разность разделить на постоянное число – лучше величину интервала

3. исчисленную среднюю в обратной последовательности умножить на постоянное число и прибавить произвольную постоянную величину

, где m₁ – момент первого порядка,

Структурные средние величины – мода и медиана

Мода и медиана для характеристики структуры совокупности.

Мода (Мо) - это наиболее часто встречающаяся величина признака в совокупности; она величина конкретная, имеющая свое определенное место; находится в дискретном и интервальном ряду. В интервальном вариационном ряду модой приближенно считают центральный вариант так называемого модального интервала, который имеет наибольшую частоту, в пределах этого интервала надо найти то значение признака, которое является модой, конкретное значение моды определяется формулой:

Мо = , где Х_Мо – нижняя граница модального интервала,

h – величина интервала, f_Mo – частота модального интервала, f_-1 – частота предмодального интервала, f₊₁ –частота послемодального интервала.

Медиана (Ме) – это величина которая делит численность упорядоченного вариационного ряда на 2 равные части: одна часть имеет значения варьирующего признака меньше, чем средний вариант, а другая – большая. Она рассчитывается для дискретного и интервального ряда. ДЛЯ ДИСКРЕТНОГО:1)для ранжированного ряда с нечетным числом членов медианой является вариант расположенный в центре ряда. 2) для ранжированного ряда с четным числом членов медианой будет среднеарифметическая из 2-х смежных вариант ближе к середине. В ИНТЕРВАЛЬНОМ РЯДУ порядок нахождения медианы следующий:

1) расположить индивидуальные значения признака по ранжиру;

2) определить для данного ряда накопленные частоты;

3) по данным о накопленных частотах найти медианный интервал, т.к. медиана делит ряд пополам, то она там где накопленная частота составляет половину (это ее порядковый номер). Ме = , где Х_Ме – нижняя граница медианного интервала, - порядковый номер медианы, S_Ме-1 – сумму накопленных частот предшествующих медианному интервалу (кумулятивные частоты), f_Me – частота медианного интервала.

Показатели вариации.

Вариация признака – это различие индивидуальных значений признака внутри изучаемой совокупности. Два ряда распределения могут иметь одинаковую среднюю величину, но в первом ряду отдельные значения признака близко примыкают к средней арифметической и мало от нее отличаются, а в другом отдельные значения далеко отстают от средней – значит она плохо представляет всю совокупность и является ненадежной характеристикой. Показатели вариации служат характеристикой типичности надежности самой средней. Чем меньше вариация, тем средняя более показательна, типична и наоборот – чем больше индивидуальные значения признака колеблются вокруг средней тем она менее типична. Показатели вариации служат для характеристики равномерности работы предприятия. Степень близости данных отдельных единиц к средней измеряется рядом абсолютных средних и относительных показателей:

I) абсолютные и средние показатели вариации:

1. размах вариации,

2. средние линейные отклонения,

3. дисперсии,

4. средние квадратичные отклонения.

II) относительные показатели вариации – коэффициент вариации.

Размах вариации представляет собой разность между наибольшим и наименьшим значением признака. R= X_max-X_min размах вариации зависит только от 2-х крайних значений признака, поэтому он недостаточно правильно отражает колеблемость.

Среднее линейное отклонение представляет собой среднюю из абсолютных величин отклонений всех значений от их среднеарифметической без учета знака отклонений: (простое), (взвешенное).

Дисперсия – это средний квадрат отклонений каждой величины от средней арифметической: (простая), (взвешенная).

Среднеквадратичное отклонение – это корень квадратный из дисперсии: (простое), (взвешенное).

Дисперсия и среднеквадратичное отклонение является общепринятыми мерами вариации признака; среднеквадратичное отклонение является мерилом надежности средней, чем меньше среднеквадратичное отклонение, тем лучше средняя арифметическая отражает собой всю совокупность.

Коэффициент вариации – это отношение среднеквадратичного отклонения к средней величине: . По его значению можно охарактеризовать однородность совокупности: если он не более 33,3%, то совокупность однородна и средняя типична.

Математические свойства дисперсии:

1. если из всех значений вариант вычесть постоянное число, то дисперсия от этого не изменится

2. если все значения вариант разделить на какое-то постоянное число а то дисперсия уменьшится от этого в а² раз

3. дисперсия от средней всегда меньше дисперсии исчисленных от любых других величин и в этом случае при А=0 формула дисперсии имеет вид: 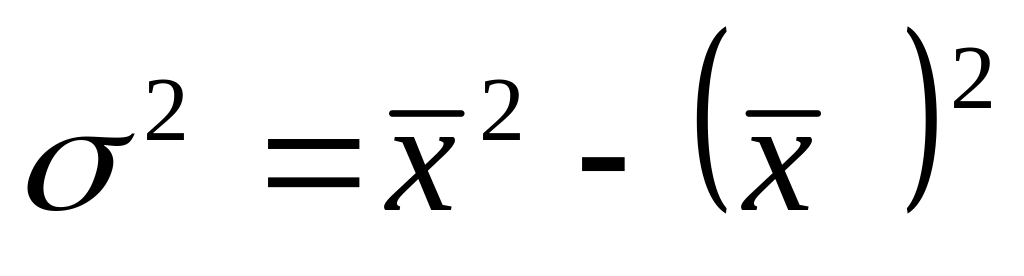, где = - средний квадрат значений признака;

= - среняя арифметическая взвешенная.

Способ отсчета от условного нуля или способ моментов применим при условии равных интервалов, используя 2-е свойство дисперсии, разделив все варианты на величину интервала получим формулу , где m_{1 =} - первый начальный момент; - второй начальный момент. Формула дисперсии методом отсчета от условного нуля: