32. Свойство равномерно сходящихся функциональных рядов.

1) Сумма правильно сходящегося ряда есть функция непрерывная в области сходимости.

Свойства почленного дифференцирования и интегрирования правильно сходящихся рядов.

2) Если ряд сходится равномерно к некоторой непрерывной функции S(x), и ряд из производных так же равномерно сходится, то его сумма S^*(x) равна производной от суммы исходного ряда S*(x) = =( )'= S'(x)

3) Если ряд сходится равномерно к некоторой непрерывной функции S(x), то ряд полученый из данного путем почленного интерирования равномерно сходится и имеет сумму S**(x), равную интегралу от суммы исходного ряда

S**(x)= = =

33. Ортогональная система функций:

Определение: последовательность функций называется ортогональной на отрезке , если

СМ. «38. Тригонометрический ряд Фурье» (последний вопрос)

34. Теорема Дирихле. Условия Дирихле.

Пусть ограниченная функция удовлетворяет на условиям:

1. интервал можно разбить на конечное число интервалов, в которых функция – непрерывная и монотонная.

2. если x_o т. разрыва функции , то 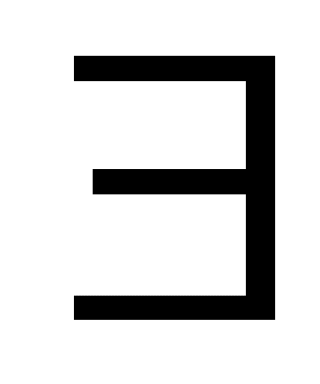пределы 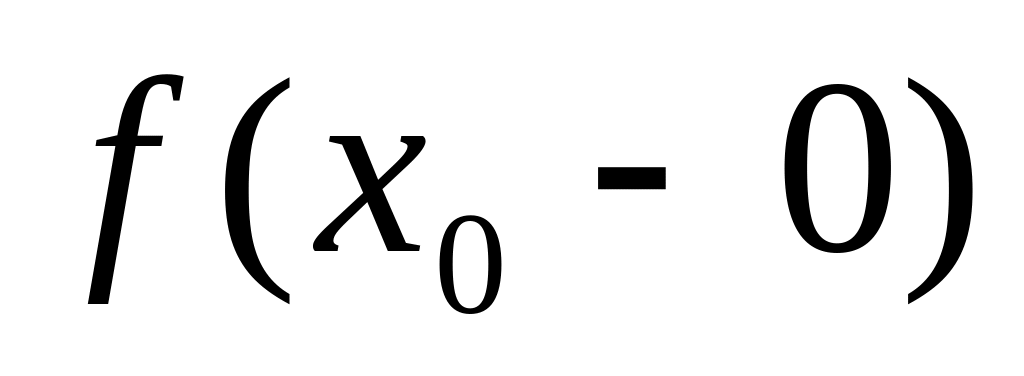, 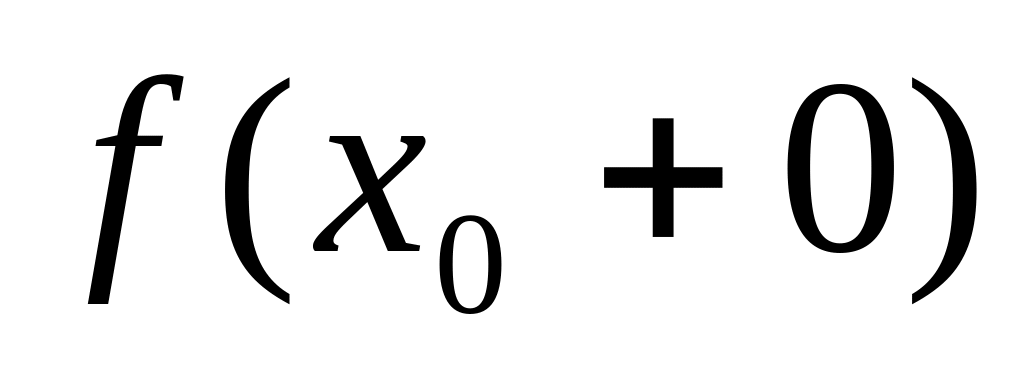. Т.е точка x₀ – т.разрыва 1 рода.

Т огда ряд Фурье функции сходится и имеет место равенство

Замечание. Если представить функцию, периодически продолженную на всю ось Ox c периодом , то утверждение теоремы будет справедливо .

35. Степенные ряды. Область сходимости. Радиус сходимости.

Функциональные ряды вида называются степенным рядом по степеням(z-z₀), где a₁ a₂... a_n R -коэффициенты степенного ряда , называются степенными рядами.

При z₀=0 получим .Степенной ряд при z=0 всегда сходится, если x не равен 0 то ряд может как сходиться так и расходиться.

Поскольку замена (z-z₀)=t может свести к виду то мы будем рассматривать ряд такого вида.

Областью сходимости ряда является интервал (-R, R), В каждой точке этого интервала ряд сходится абсолютно, а на интервалах — расходится

Интервал (-R, R) называется интервалом сходимости ряда, a R — его радиусом сходимости. Для некоторых рядов интервал сходимости вырождается в точку (R= 0), для других — охватывает всю ось OX(R= ). При х= R ряд может и сходиться, и расходиться (вопрос решается для каждого конкретного ряда).

36. Ряд Тейлора, область сходимости. Достаточный признак сходимости ряда Тейлора.

Всякая функция при соблюдении определённых условий в интервале, содержащем точку ,может быть представлена в нём в виде степенного ряда, и этот ряд будет её рядом Тейлора.

Опр-е: Рядом Тейлора функции f(x) называется степенной ряд вида:

Ряды Тейлора и Маклорена есть разложение функции в ряд по степеням ( ) и соответственно ,или представление функции в окрестности точек или степенным рядом.

Коэффициенты рядов Тейлора и Маклорена вычисляются через значения производных функции всех порядков в точках = и = 0 соответственно. Но существование производных любого порядка не является достаточным условием разложимости функции в ряд Тейлора.

Достаточный признак сходимости ряда Тейлора:

Всякая функция ,бесконечно дифференцируемая в интервале < r,может быть разложена в этом интервале в сходящийся к ней степенной ряд, называемый рядом Тейлора, если в этом интервале остаток ряда стремится к нулю .

Остаток ряда Тейлора можно записать в форме Лагранжа

Условие выполняется, если производные всех порядков функции ограничены некоторым числом