2 3. Теорема о существовании и единственности решения ду в полных дифференциалах.

24. Определитель Вронского.

Определитель Вронского — определитель следующей матрицы:

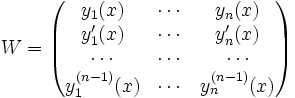
Применяется для решения дифференциальных уравнений.

Имеют место следующие теоремы: Пусть — (n-1) раз дифференцируемые функции, тогда:

• Если линейно зависимы на X, то det(W) = 0.

• Если det(W) = 0 хотя бы для одного 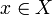, то линейно зависимы на X.

Или:

• Определитель Вронского либо тождественно равен нулю, и это означает, что линейно зависимы, либо не обращается в нуль ни в одной точке X, что означает линейную независимость функций .

25. Линейные однородные дифференциальные уравнения n-го порядка с постоянными коэффициентами. Вид частных решений, характеристическое уравнение

ЛОДУ с постоянными коэффициентами

у⁽ⁿ⁾ + P₁y^(n-1) +…+ P_n-1 y’ + P_n y = 0, где все P_i (i= )= const

будем искать частное решение y=e^kx , к – неизвестная постоянная

y’=ke^kx

y’’=k²e^kx

……

y⁽ⁿ⁾=k⁽ⁿ⁾ e^kx

k⁽ⁿ⁾ e^kx + P₁k^(n-1) e^kx + … + P_ne^kx = e^kx(k⁽ⁿ⁾ + P₁k^(n-1) + … + P_n) = 0

e^kx 0 => k⁽ⁿ⁾ + P₁k^(n-1) + … + P_n = 0, (1)

• y=e^kx - решение ДУ

(1) – характеристическое уравнение для ЛОДу с постоянными коэффициентами, выражения слева характеристический многочлен.

Решением характеристич уравнения (1) дает систему частных решений ЛОДу, структура ФСР зависит от вида корней характер уравнения.

(1) – алгебраическое уравнение n-ой степени, может иметь не более, чем n корней, обознач-м эти корни характеристического уравнения через k₁ ,k₂ …k_n

Возможны случай

1)все корни хар-го уранения вещественны и различны

2)все корни различны, но среди них есть комплексные

3)среди действительных корней имеются кратные

4)среди комплексных корней есть кратные

Общий алгоритм решения ЛОДу с постоянным коэффициентом

1) составим характер уравнение : y=e^kx , k⁽ⁿ⁾ + P₁k^(n-1) + … + P_n = 0

2) найти корни характер уравнения k₁ ,k₂ …k_n

3) по характеру корней находим частное линейно-независимое решение по таблице 1

4) подставляем частное решение на основе Теоремы о структуре общего решения ЛОДУ и получаем общее решение y =

№	Вид корня	Соответственное решение
1	Действ корень кратности 1	ekx
2	Пара корней a bi;кратнос 1	eаxcosbx , eаxsinbx
3	Действит корень кратност α	ekx, хekx, х2ekx, х3ekx,…, хα-1ekx
4	Пара сопряж корней α a bi	eаxcosbx , eаxsinbx хeаxcosbx , хeаxsinbx х2eаxcosbx , х2eаxsinbx хα-1eаxcosbx , хα-1eаxsinbx

26.Теорема о существовании и единственности решения задачи Коши д.У. Порядка выше первого.

Если функция (n+1)-й переменной в некоторой области (n+1)-мерного пространства непрерывна и имеет непрерывные Ч.П. по переменным , ( ), то для любой фиксированной точки этой области и при том единственное решение уравнения .

Определенное на и удовлетворяет начальным условиям , , .

Д.У. 2-го порядка c начальными условиями , . Через точку проходят бесконечно много интегральных кривых, и задаем и выбираем единственную интегральную кривую.