2. Аналитические показатели ряда динамики.
Поскольку ряды динамики состоят из n-го числа варьирующих уровней, то они, как всякая статистическая совокупность, нуждаются в обощённии, в некоторых обобщённых характеристиках.
Для любого ряда динамики, прежде всего можно рассчитать такой обобщённый показатель, как средний уровень ряда.
Для интервальных рядов средних величин средний уровень рассчитывается как средняя арифметическая из отдельных уровней, т.е. если отдельные уровни обозначились через Yi то средний уровень (Y) выразится как, где n число уровней.
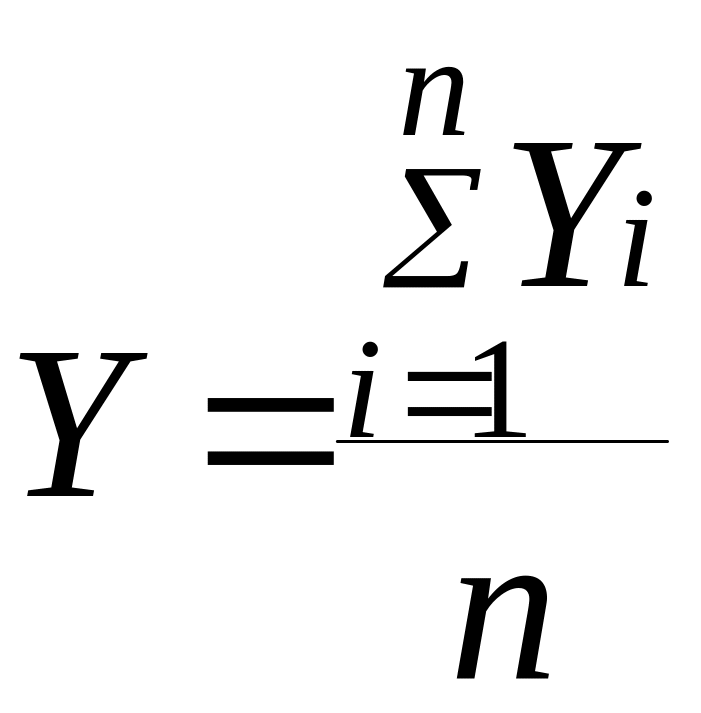
Несколько по иному приходиться рассчитывать средний уровень для моментных рядов. Если исходить из рассмотрения простейшего случая, когда имеются данные лишь на начало и конец какого-либо периода, то в этом случае средний уровень определяется с помощью средней хронологической по следующей формуле:
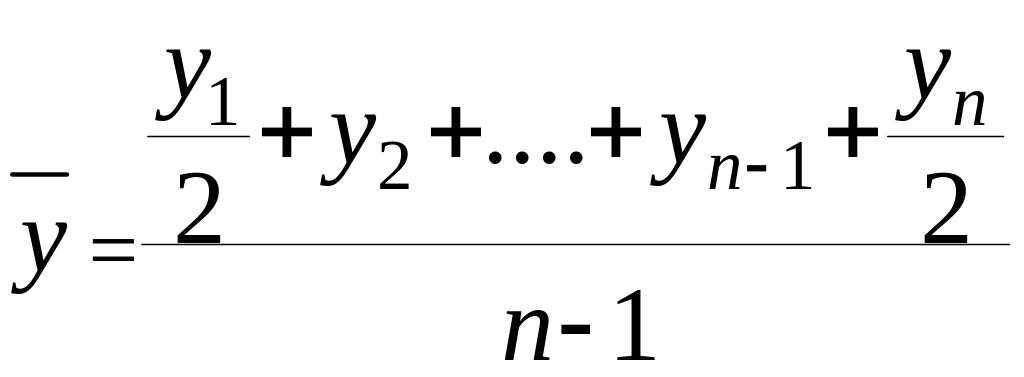
Применение данной формулы предполагает равные отрезки времени между датами (моментами), к которым относятся уровни моментного ряда. В случае же неравных интервалов между датами среднюю хронологическую для моментных рядов следует рассчитывать как среднюю арифметическую взвешенную, приняв в качестве весов отрезки времени между датами.
Если для ряда рассчитан средний уровень, то, естественно, отдельные уровни ряда будут отличаться от него (варьировать). Поэтому, как для любой статистической совокупности вообще, в динамических рядах можно определять колеблемость уровней при помощи известных уже нам среднего квадратического отклонения ( ) и коэффициента вариации (V).
Они выражаются формулами:
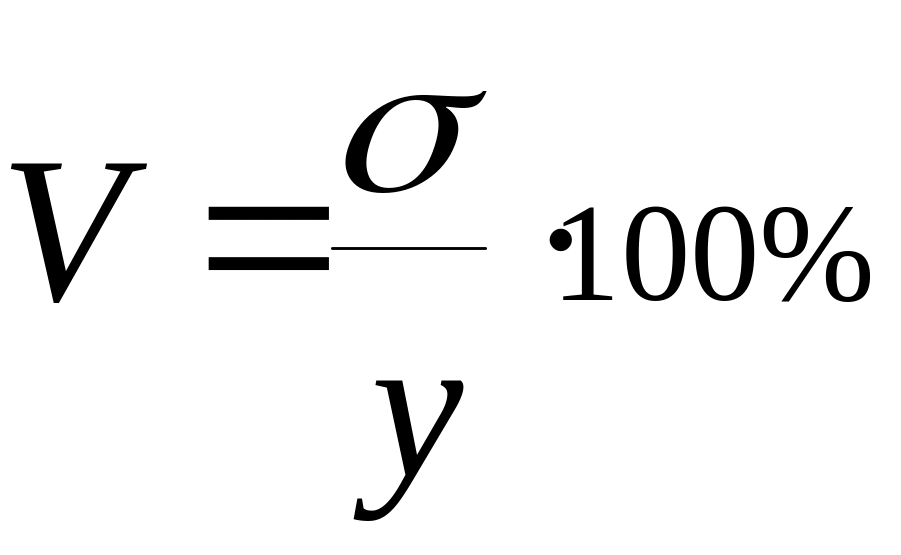
Средний уровень ряда, среднее квадратическое отклонение и коэффициент вариации - обобщающие показатели. Вместе с тем при изучении рядов динамики важно проследить направлением и размером изменений уровней во времени. С этой целью для динамических рядов рассчитывают следующие показатели: абсолютный прирост, темп роста, темп прироста.
Абсолютный прирост рассчитывается как разность между двумя уровнями ряда, т.е. Y = Yi - Yi-1. Он показывает, на сколько единиц в абсолютном выражении уровень одного периода больше или меньше какого-то предыдущего уровня и, следовательно, может иметь знак <+> (при увеличении уровней) или <-> (при уменьшении уровней).
Темп роста - относительный показатель (выражаемый в коэффициентах или процентах), получающийся в результате деления двух уровней, показывает, во сколько раз уровень данного периода больше или меньше базисного уровня или сколько процентов составил уровень данного периода по сравнению с базисным уровнем. В качестве базисного уровня (т.е. того уровня, с которым производится сравнение) в зависимости от цели исследования может приниматься какой-то постоянный для всех уровень (часто начальный уровень ряда) либо для каждого последующего предшествующий ему. Они могут быть рассчитаны следующими формулами:
В первом случае говорят о базисных темпах роста, а во втором случае - о цепных темпах роста.
Темп прироста - относительный показатель, показывающий, на сколько процентов один уровень больше (или меньше) базисного уровня. Этот показатель можно рассчитать путём вычитания 100% из темпа роста или как процентное соотношение абсолютного прироста к тому базисному уровню, по отношению, с которым абсолютный прирост рассчитан.
Для названных выше показателей, в свою очередь, тоже могут рассчитываться обобщающие показатели в виде средних величин: среднегодовой абсолютный прирост, среднегодовой коэффициент и темп роста и прироста.