
- •1.Классфификация кинематических цепей
- •2.Виды нагрузок электропривода и их классификация
- •3. Обобщенные математические модели механической части эп
- •Математическая модель и структурная схема двухмассовой модели эп.
- •5.Передаточные функции двухмассовой модели
- •6.Динамические свойства двухмассовой модели эп
- •7 .Модель,структурная схема и уравннеие движения одномассовой системы эп
- •9 .. Приведение сил, моментов сопротивления, моментов инерции и масс к валу эд для линейных пм
- •10.Приведение сил, моментов сопротивления, моментов инерции и масс к валу эд для нелинейных пм
- •13 Учет потерь в передаче.
- •14. Уточненный метод учета потерь в передаче.
- •11 Оптимальное передаточное число редуктора
- •По минимуму времени переходного процесса:
- •12Оптимальное передаточное числопо критерию минимум габарита эд
- •15. Статическая устойчивость работы эп
- •16.Механические переходные процессы эп при линейном динамическом моменте
- •18.Электромеханическая постоянная времени
- •20.Угол поворота вала электродвигателя за время переходного процесса.
- •21. Механические переходные процессы эп при нелинейном динамическом моменте
- •Теперь получаем дифференциальное уравнение:
- •С учетом (1.357) это уравнение принимает вид
- •При отсутствии диссипативных сил на основании (1.385) получаем
- •25.Уравнения напряжений, потокосцеплений и электромагнитного момента оэм.
- •26.Электромеханическая связь в эп
- •30. Модель оэм в осях u-V и её уравнения напряжений,потокосцепдений
- •31.Выражения электромагнитного момента оэм через скалярные величины и пространственные векторы.
- •33. Эквивалентная схема оэм в осях X-y для установившегося режима работы
- •Поскольку
- •34. Фазные преобразования переменных
- •Для трехфазной трехпроводной системы
- •35. Инвариантность мощности в преобразованиях уравнений оэм от осей к осям u-V
- •36 Режимы работы электродвигателей и ограничения на электромеханические преобразования энергии
- •37. Модель дпт нв в осях и её уравнения
- •38. Математическая модель дпт нв и структурная схема дпт нв в осях
- •40. Статические характеристики дпт нв
- •43 Математическая модель дпт пв в осях α–β.
- •44.Структурная схема линеаризованной модели дпт пв
- •45.Статические характеристики дпт пв при ненасыщенной магнитной системе.
- •47. Тормозные режимы работы дпт пв
- •48. Математическая модель дпт св в осях а-в
- •49. Статические характеристики дпт св
- •52. Статические характеристики ад. Механическая хар-ка и полная механическая мощность ад.
- •54. Влияние параметров на свойство и механическую характеристику ад
- •53. Электромеханические характеристики ад.
- •55. Характеристики и свойства асинхронного двигателя при питании от источника тока.
- •56.. Структурная схема линеаризованного ад при питании от источника напряжения.
- •58. Тормозные режимы ад: рекуперативное торможение и торможение противовключением
- •57.. Динамическое торможение ад при независимом возбуждении.
- •39.Уравнения , электромеханические и механические характеристики дпт нв при постоянном магнитном потоке. Структурная схема дпт нв
- •1. 1.Классфификация кинематических цепей 1
18.Электромеханическая постоянная времени
ЭЛЕКТРОМЕХАНИЧЕСКАЯ
ПОСТОЯННАЯ ВРЕМЕНИ опредедяется из
выражения Тм =
,
и след-но зависитот характера
статического момента.только при М
с=const,
c=0,эелектромеханическая
постоянная эп определяется модулем
жёсткости мех хар-ки электродвигателя
Тм =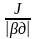 ,
,
Эл.мех. постоянну. Можно определить из графиков:
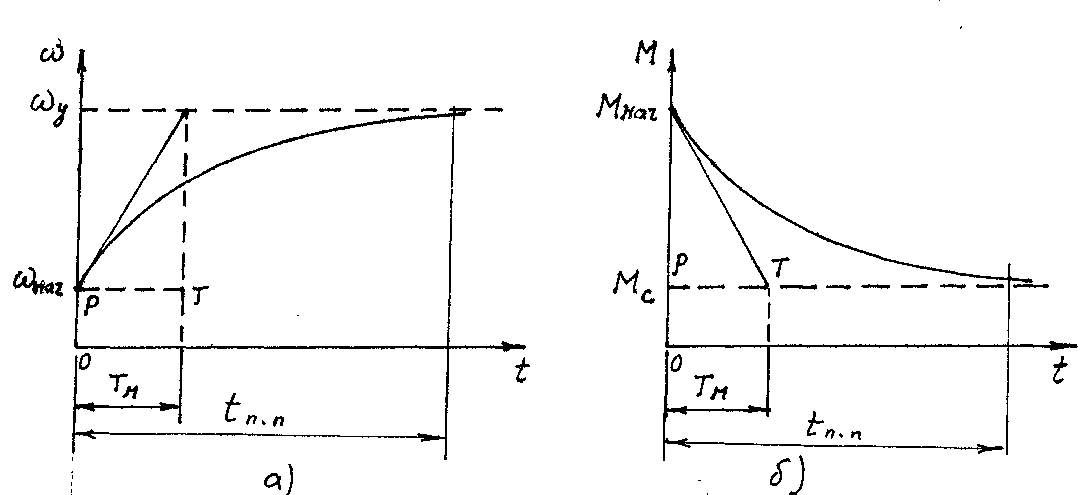
19.ВРЕМЯ РАЗГОНА И ТОРМОЖЕНИЯ ЭП
Пологая в общем случае, что динамический момент является функцией
скорости, т. е. Мдин(), время переходного процесса tп.п. при изменении скорости от 1 до 2 находим из основного уравнения движения электропривода (1.72):
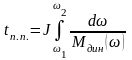 .
.
а)
Мдин()
= Мдин
= const,
в этом случае
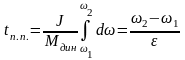 ,
,
где
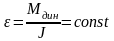 .
- угловое ускорение.
.
- угловое ускорение.
б) Мдин = +, тогда
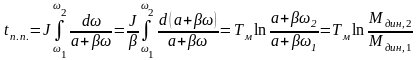 .
.
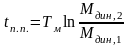 ,
при
> 0
,
при
> 0
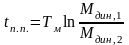 ,
при b
< 0
,
при b
< 0
20.Угол поворота вала электродвигателя за время переходного процесса.
Угловой путь j за время переходного процесса определяем, интегрируя скорость:
 ,
т.к.
,
т.к.
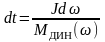 ,
то
,
то
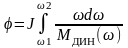
Частные случаи:
А)
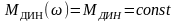
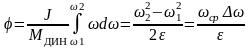 ;
;
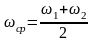 ,
,
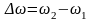 ,
,
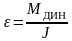
Угловой путь за время переходного процесса можно представить:
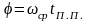 ,
где wСР
– средняя скорость за время переходного
процесса tп.п.
,
где wСР
– средняя скорость за время переходного
процесса tп.п.
Б)
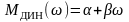
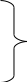
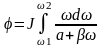 ,
проинтегрировав, получаем:
,
проинтегрировав, получаем:
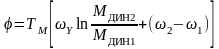 при b>0
при b>0
при b<0
где
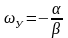
Иногда необходимо знать не только величину углового пути за время переходного процесса, но и характер его изменения в переходном процессе:
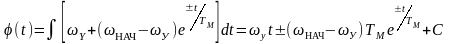 ,
,
где С – постоянная интегрирования, определяется из начальных условий:
при t=0, j=jНАЧ:
![]() ,
,
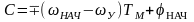 .
.
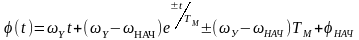
где знак «+» соответствует b>0, а «-» b<0
21. Механические переходные процессы эп при нелинейном динамическом моменте
Нелинейный динамический момент может быть из-за нелинейности механической характеристики электродвигателя, нелинейности статического момента или нелинейности обеих характеристик. применяются два: метод кусочно-линейной аппроксимации и метод конечных разностей. Рассмотрим их.
а) Метод кусочно-линейной аппроксимации.
П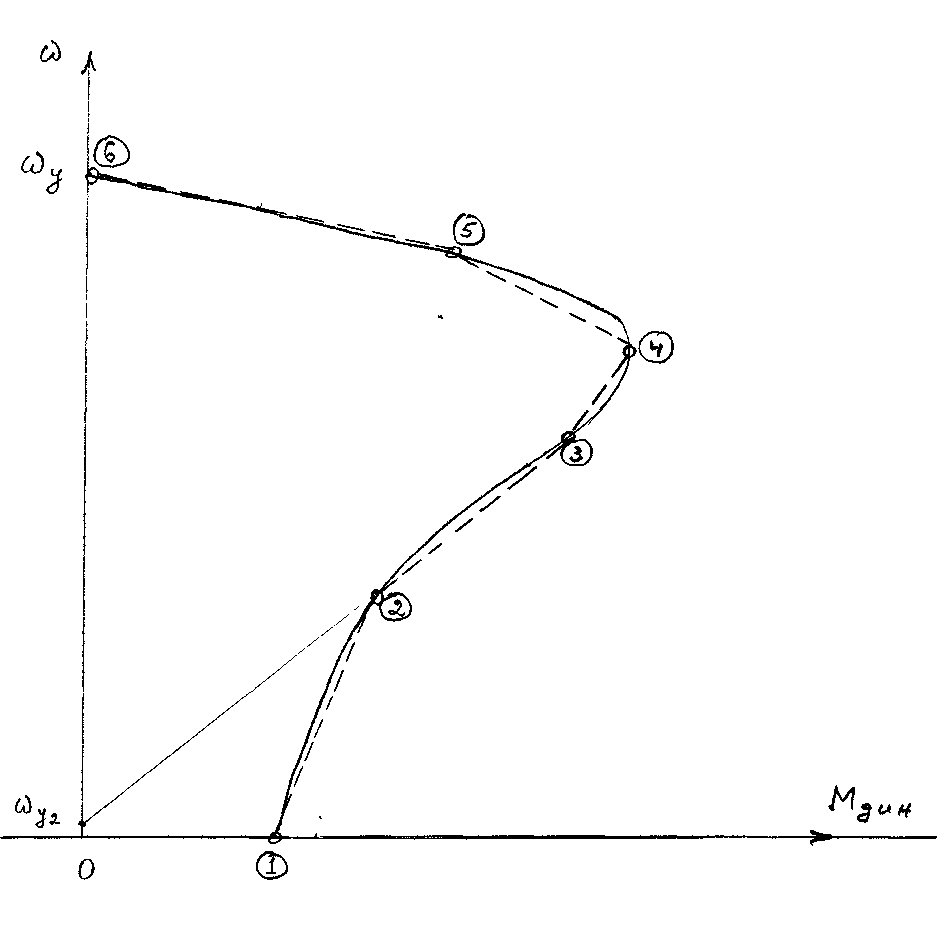 усть
нелинейный динамический момент имеет
вид, представленный на рис. 1.29. На кривой
Мдин (w)
выбираем такое количество n
точек, чтобы ломаная кусочно-линейная
кривая 1 – 2 – 3 – 4 – 5 – 6 наиболее
близко отражала реальную функцию Мдин
(w).
Для каждого j-ого
отрезка этой кривой, где j=1,2…n-1,
можно записать выражения:
усть
нелинейный динамический момент имеет
вид, представленный на рис. 1.29. На кривой
Мдин (w)
выбираем такое количество n
точек, чтобы ломаная кусочно-линейная
кривая 1 – 2 – 3 – 4 – 5 – 6 наиболее
близко отражала реальную функцию Мдин
(w).
Для каждого j-ого
отрезка этой кривой, где j=1,2…n-1,
можно записать выражения:
-жесткости
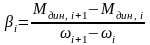 ,
,
-
электромеханической постоянной времени
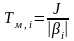 ,
,
-
установившегося значения скорости
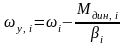 ,
,
- времени переходного процесса
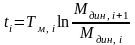 при
b
> 0
при
b
> 0
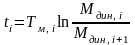 при
b
< 0
при
b
< 0
где i – номер начала отрезка, i+1 – номер конца отрезка, j=1,2…n-1 – номер отрезка кусочно-линейной кривой
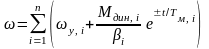 ,
,
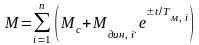 ,
,
где 0 £ t £ t i. , My,j=MC(wy,j)
знак «+» в экспоненте соответствует bj > 0, а «-» - bj < 0
Кривые w (t) и M (t) представляют собой сумму кривых wi (t) и Mi (t), рассчитанных для отдельных участков, а время переходного процесса определяется суммой:
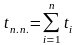 .
.
б) Метод конечных разностей
Уравнение движения электропривода (1.72) записывается в конечных разностях
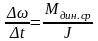 откуда
находим
откуда
находим
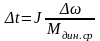 .
.
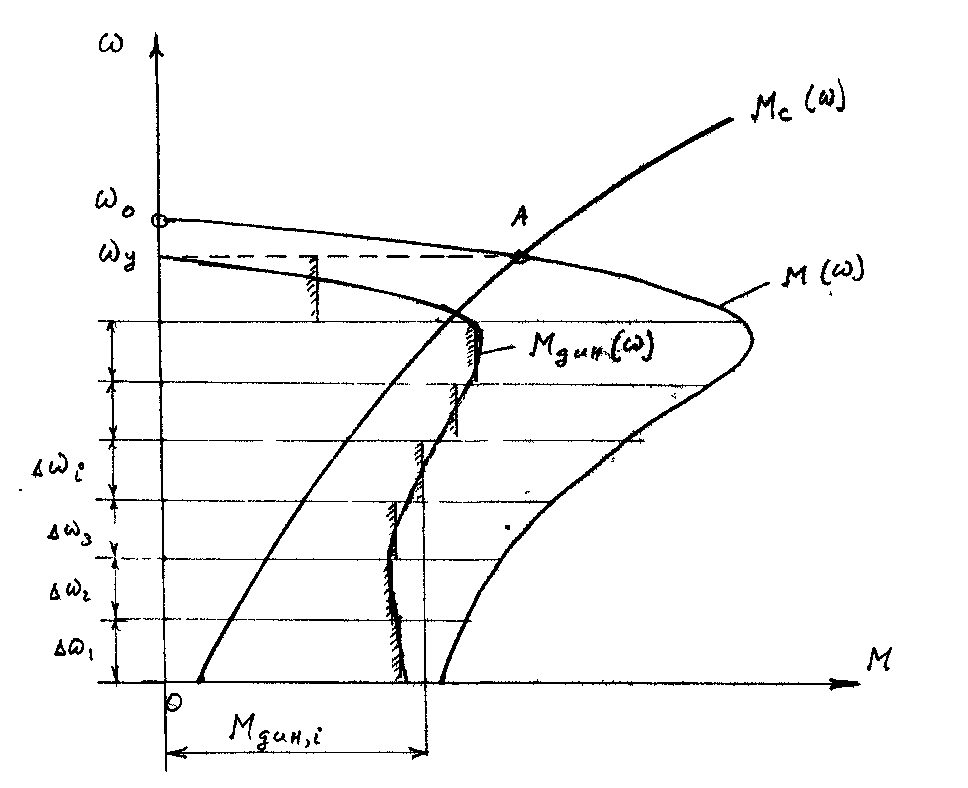
Диапазон изменения скорости в переходном процессе разбивается на несколько (в среднем 15 – 20) участков рис.1.30. Обычно в целях удобства их берут равными. Для каждого участка определяется среднее значение динамического момента
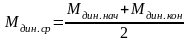 .
.
Поскольку динамический момент на каждом участке постоянный, то скорость, как мы уже знаем, изменяется на участке по линейному закону. Например, для i-ого участка скорость электродвигателя будет определяться уравнением
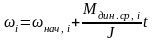 ,
,
где 0 £ t £ Dt i.
Угол поворота вала электродвигателя за время переходного процесса на i-ом участке будет равен
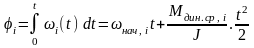 .
.
Зависимость электромеханического момента от времени М (t) находится для каждого значения скорости wi (t) по механической характеристике двигателя w (М).
=22МЕХАНИЧЕСКИЕ ПЕРЕХОДНЫЕ ПРОЦЕССЫ 2Х МАССОВОЙ СИСТЕМЫ ЭП
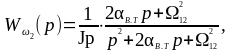 (1.49)
(1.49)
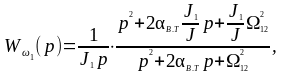 (1.50)
(1.50)
Передаточные функции по управляющему и возмущающему воздействию, при этом возмущающее воздействие принимается равным нулю. При использовании этих передаточных функций рассматривается переходный процесс при холостом ходе. На основании передаточной функции (1.50) запишем операторное уравнение
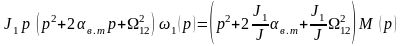
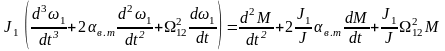
Будем рассматривать переходной процесс при М = const, тогда
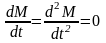 è
è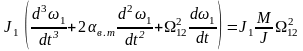 .
.
Поскольку Мс = 0, то М = Мдин, а это позволяет записать
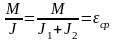 ,
,
где eср – среднее ускорение двухмассовой системы.
