
- •1.Классфификация кинематических цепей
- •2.Виды нагрузок электропривода и их классификация
- •3. Обобщенные математические модели механической части эп
- •Математическая модель и структурная схема двухмассовой модели эп.
- •5.Передаточные функции двухмассовой модели
- •6.Динамические свойства двухмассовой модели эп
- •7 .Модель,структурная схема и уравннеие движения одномассовой системы эп
- •9 .. Приведение сил, моментов сопротивления, моментов инерции и масс к валу эд для линейных пм
- •10.Приведение сил, моментов сопротивления, моментов инерции и масс к валу эд для нелинейных пм
- •13 Учет потерь в передаче.
- •14. Уточненный метод учета потерь в передаче.
- •11 Оптимальное передаточное число редуктора
- •По минимуму времени переходного процесса:
- •12Оптимальное передаточное числопо критерию минимум габарита эд
- •15. Статическая устойчивость работы эп
- •16.Механические переходные процессы эп при линейном динамическом моменте
- •18.Электромеханическая постоянная времени
- •20.Угол поворота вала электродвигателя за время переходного процесса.
- •21. Механические переходные процессы эп при нелинейном динамическом моменте
- •Теперь получаем дифференциальное уравнение:
- •С учетом (1.357) это уравнение принимает вид
- •При отсутствии диссипативных сил на основании (1.385) получаем
- •25.Уравнения напряжений, потокосцеплений и электромагнитного момента оэм.
- •26.Электромеханическая связь в эп
- •30. Модель оэм в осях u-V и её уравнения напряжений,потокосцепдений
- •31.Выражения электромагнитного момента оэм через скалярные величины и пространственные векторы.
- •33. Эквивалентная схема оэм в осях X-y для установившегося режима работы
- •Поскольку
- •34. Фазные преобразования переменных
- •Для трехфазной трехпроводной системы
- •35. Инвариантность мощности в преобразованиях уравнений оэм от осей к осям u-V
- •36 Режимы работы электродвигателей и ограничения на электромеханические преобразования энергии
- •37. Модель дпт нв в осях и её уравнения
- •38. Математическая модель дпт нв и структурная схема дпт нв в осях
- •40. Статические характеристики дпт нв
- •43 Математическая модель дпт пв в осях α–β.
- •44.Структурная схема линеаризованной модели дпт пв
- •45.Статические характеристики дпт пв при ненасыщенной магнитной системе.
- •47. Тормозные режимы работы дпт пв
- •48. Математическая модель дпт св в осях а-в
- •49. Статические характеристики дпт св
- •52. Статические характеристики ад. Механическая хар-ка и полная механическая мощность ад.
- •54. Влияние параметров на свойство и механическую характеристику ад
- •53. Электромеханические характеристики ад.
- •55. Характеристики и свойства асинхронного двигателя при питании от источника тока.
- •56.. Структурная схема линеаризованного ад при питании от источника напряжения.
- •58. Тормозные режимы ад: рекуперативное торможение и торможение противовключением
- •57.. Динамическое торможение ад при независимом возбуждении.
- •39.Уравнения , электромеханические и механические характеристики дпт нв при постоянном магнитном потоке. Структурная схема дпт нв
- •1. 1.Классфификация кинематических цепей 1
11 Оптимальное передаточное число редуктора
По минимуму времени переходного процесса:
первый способ: (ЭД М=const, Jд=const) (Исполн-й мех-м Mн,wн,Jн)
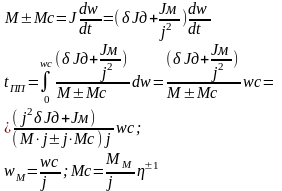
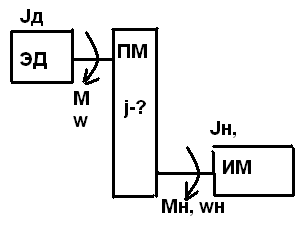
+ торможение , - разгон
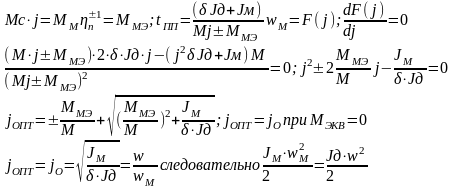
При оптимальном j и отсуствия момента нагрузки на валу, кинетическая энергия механизма = кинетической энергии ЭД вместе с редуктором
второй способ (ЭД P =const) (Исполн-й мех-м Mн,wн,Jн)
М=const;
М=Мном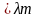 ;
;
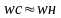
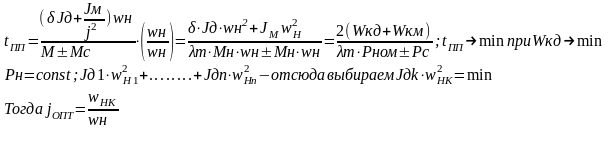
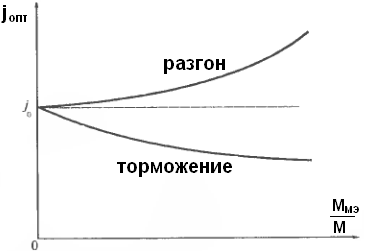
12Оптимальное передаточное числопо критерию минимум габарита эд
угловое ускорение:
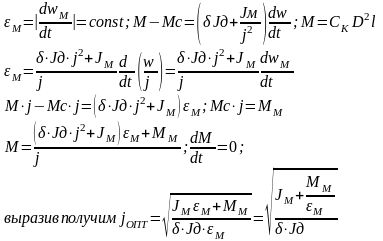
при
отсуствии нагрузки на выходном валу
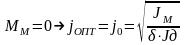
фиктивный момент инее
рции
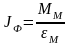
тогда
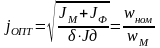 следовательно
следовательно
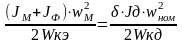
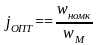
15. Статическая устойчивость работы эп
 Под
статической устойчивостью понимают
способность электропривода возвращаться
в равновесное состояние после устранения
возмущающего воздействия. Статическая
устойчивость анализируется на основе
основного уравнения движения электропривода
Под
статической устойчивостью понимают
способность электропривода возвращаться
в равновесное состояние после устранения
возмущающего воздействия. Статическая
устойчивость анализируется на основе
основного уравнения движения электропривода
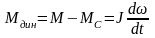 при
малых отклонениях от равновесного
состояния (Рис.1.21).
при
малых отклонениях от равновесного
состояния (Рис.1.21).
В установившемся состоянии
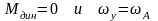
При
небольшом отклонении
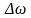 скорости от равновесного состояния
динамический момент можно представить
линейной зависимостью
скорости от равновесного состояния
динамический момент можно представить
линейной зависимостью
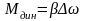 ,
где
,
где
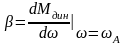 ,
а скорость как
,
а скорость как
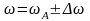 ,
,
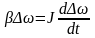 ,
интегрируя которое
,
интегрируя которое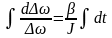 ,
,
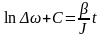 ,
,
Постоянную интегрирования С определяем из начальных условий:
при
t=0
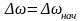 ,
тогда
,
тогда
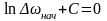 и
и
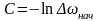 ,
,
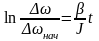 ,
или
,
или
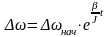 ,
,
Чтобы
работа электропривода была устойчивой,
необходимо иметь
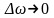 при
при
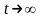 ,
а это возможно, если
,
а это возможно, если
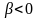 ,
т.е.
,
т.е.
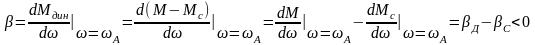 ,
,
где
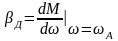 ,
,
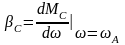 ,
,
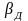 -
жесткость механической характеристики
электродвигателя в точке А;
-
жесткость механической характеристики
электродвигателя в точке А;
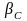 -
жесткость механической характеристики
исполнительного механизма в точке А.
-
жесткость механической характеристики
исполнительного механизма в точке А.
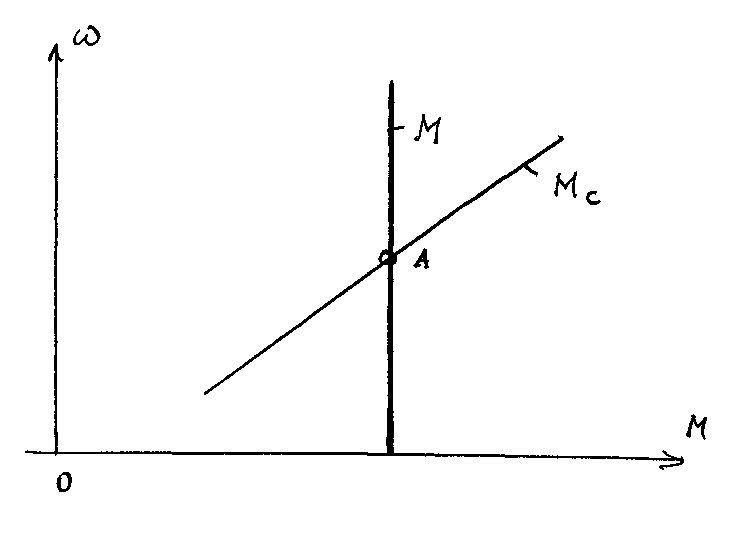
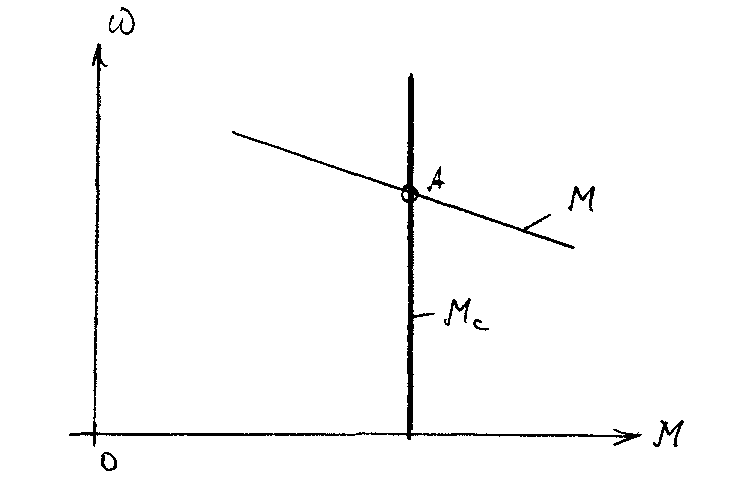
Следовательно, для устойчивой работы электропривода необходимо, чтобы в точке равновесного состояния жесткость механической характеристики электродвигателя была меньше жесткости механической характеристики исполнительного механизма.
 Рассмотрим
некоторые частные случаи.
Рассмотрим
некоторые частные случаи.
1)
М=Const,
тогда
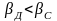 или
или
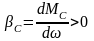
2)
Мс=Const,
тогда
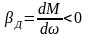
Так как для статической устойчивости необходимо иметь , то при отклонении скорости от точки равновесия в положительном направлении
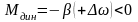 ,
,
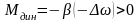 ,
,
Для механических характеристик, показанных на Рис.1.24а:
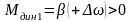 ,
,
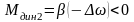 ,
,
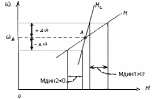
следовательно,
в точке А установившееся состояние
неустойчивое. Механическая модель
неустойчивого равновесия
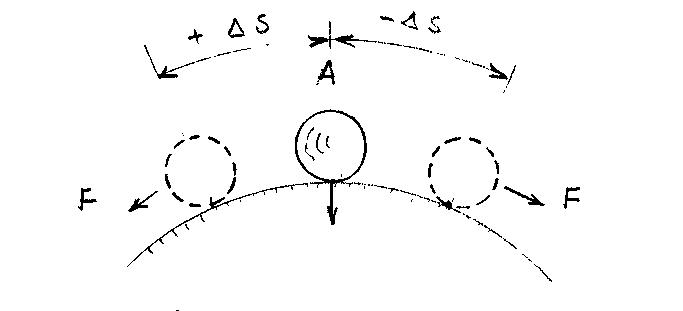
Установившееся состояние в точке А Рис.1.25а будет устойчивым, поскольку
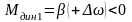 ,
,
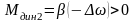 .
.
Механическая модель устойчивого равновесия приведена на Рис.1.25б.
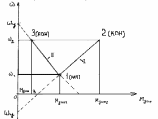
16.Механические переходные процессы эп при линейном динамическом моменте
В общем случае линейный динамический момент можно представить
зависимостью Мдин = +. ,
где =Мдин (=0)=Мк М0 ,
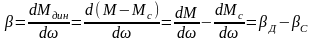 ,
,
Мк – момент электродвигателя при = 0,
Мс – статический момент при = 0,
– жесткость характеристики Мдин().
Примем, что линейный динамический момент образуется из линейного электромагнитного момента двигателя и линейного статического момента:
Mc=M0+cw
Тогда жесткости c и Д механической характеристики двигателя w(M) и статического момента Мс(w) будут постоянными величинами, причем возможны случаи, когда:
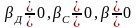
Тогда из основного уравнения ЭП:
+=J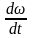 Тм =
Тм =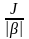 ,
,
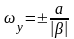 ,
,
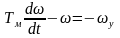
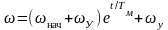 ,
,
У – установившееся значение скорости , соответствующее Мдин = 0.
нач – начальное значение скорости в переходном процессе.
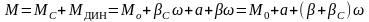
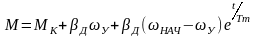
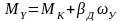
где МУ – электромагнитный момент двигателя, соответствующий скорости wУ.
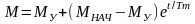
Как видно из изложенного, постоянная TM может быть положительной или отрицательной в зависимости от знака жесткости динамического момента. Но в общепринятой практике ее принимают как положительную величину, тогда:
а) для >0
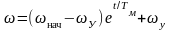
а) для <0
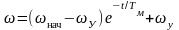
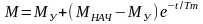
Если МС=const, то с=0, Д=0, wУ=0, MУ=МС
Практически принимаем время переходного процесса принимают:
tП.П.=(34)TM, что соответствует достижению скорости =(0,95+0,98)У
