- •1.Классфификация кинематических цепей
- •2.Виды нагрузок электропривода и их классификация
- •3. Обобщенные математические модели механической части эп
- •Математическая модель и структурная схема двухмассовой модели эп.
- •5.Передаточные функции двухмассовой модели
- •6.Динамические свойства двухмассовой модели эп
- •7 .Модель,структурная схема и уравннеие движения одномассовой системы эп
- •9 .. Приведение сил, моментов сопротивления, моментов инерции и масс к валу эд для линейных пм
- •10.Приведение сил, моментов сопротивления, моментов инерции и масс к валу эд для нелинейных пм
- •13 Учет потерь в передаче.
- •14. Уточненный метод учета потерь в передаче.
- •11 Оптимальное передаточное число редуктора
- •По минимуму времени переходного процесса:
- •12Оптимальное передаточное числопо критерию минимум габарита эд
- •15. Статическая устойчивость работы эп
- •16.Механические переходные процессы эп при линейном динамическом моменте
- •18.Электромеханическая постоянная времени
- •20.Угол поворота вала электродвигателя за время переходного процесса.
- •21. Механические переходные процессы эп при нелинейном динамическом моменте
- •Теперь получаем дифференциальное уравнение:
- •С учетом (1.357) это уравнение принимает вид
- •При отсутствии диссипативных сил на основании (1.385) получаем
- •25.Уравнения напряжений, потокосцеплений и электромагнитного момента оэм.
- •26.Электромеханическая связь в эп
- •30. Модель оэм в осях u-V и её уравнения напряжений,потокосцепдений
- •31.Выражения электромагнитного момента оэм через скалярные величины и пространственные векторы.
- •33. Эквивалентная схема оэм в осях X-y для установившегося режима работы
- •Поскольку
- •34. Фазные преобразования переменных
- •Для трехфазной трехпроводной системы
- •35. Инвариантность мощности в преобразованиях уравнений оэм от осей к осям u-V
- •36 Режимы работы электродвигателей и ограничения на электромеханические преобразования энергии
- •37. Модель дпт нв в осях и её уравнения
- •38. Математическая модель дпт нв и структурная схема дпт нв в осях
- •40. Статические характеристики дпт нв
- •43 Математическая модель дпт пв в осях α–β.
- •44.Структурная схема линеаризованной модели дпт пв
- •45.Статические характеристики дпт пв при ненасыщенной магнитной системе.
- •47. Тормозные режимы работы дпт пв
- •48. Математическая модель дпт св в осях а-в
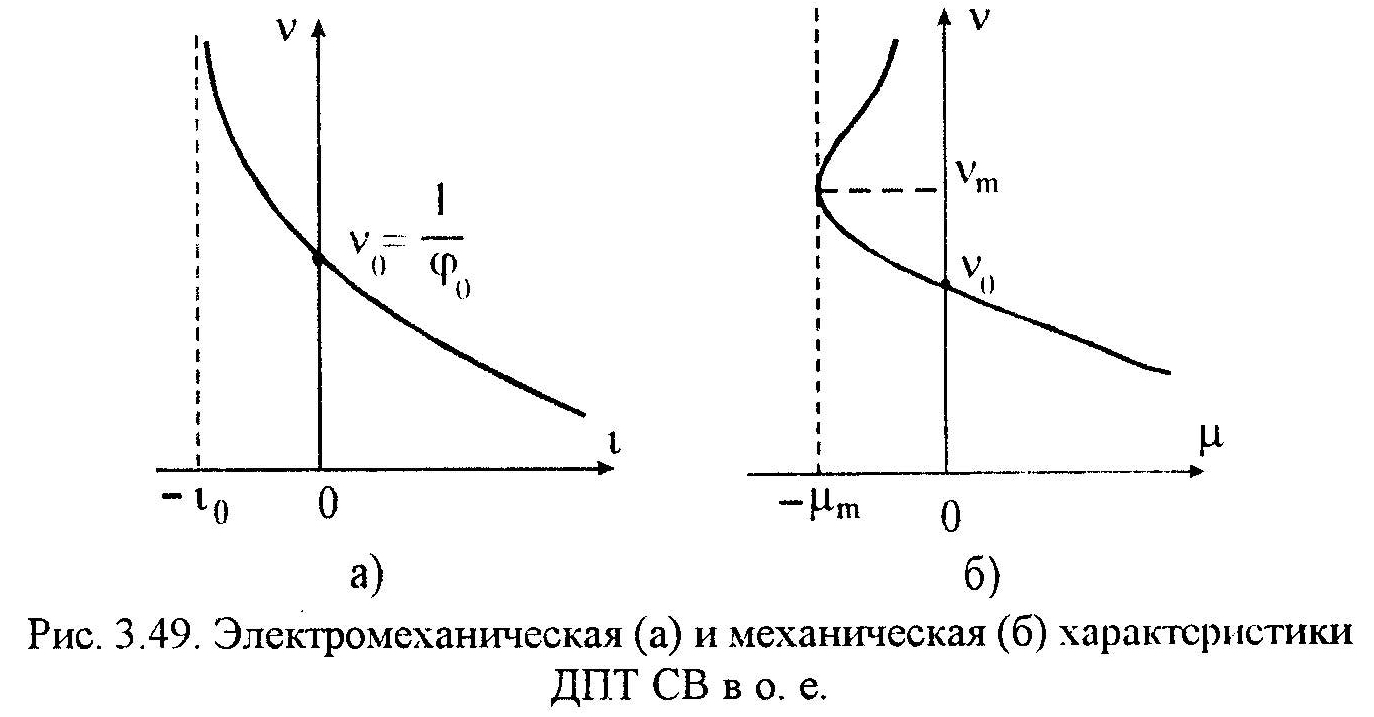
- •49. Статические характеристики дпт св
- •52. Статические характеристики ад. Механическая хар-ка и полная механическая мощность ад.
- •54. Влияние параметров на свойство и механическую характеристику ад
- •53. Электромеханические характеристики ад.
- •55. Характеристики и свойства асинхронного двигателя при питании от источника тока.
- •56.. Структурная схема линеаризованного ад при питании от источника напряжения.
- •58. Тормозные режимы ад: рекуперативное торможение и торможение противовключением
- •57.. Динамическое торможение ад при независимом возбуждении.
- •39.Уравнения , электромеханические и механические характеристики дпт нв при постоянном магнитном потоке. Структурная схема дпт нв
- •1. 1.Классфификация кинематических цепей 1
48. Математическая модель дпт св в осях а-в
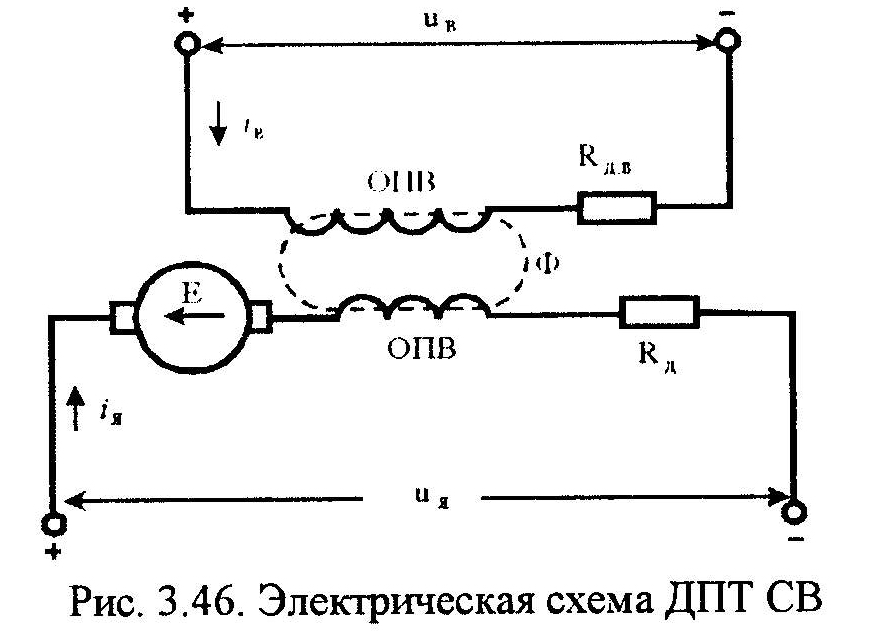
Двигатель постоянного тока смешанного возбуждения имеет две обмотки возбуждения: независимого возбуждения ОНВ и последовательного возбуждения ОПВ. Обе обмотки находятся на одном полюсе и связаны общим магнитным потоком Ф (рис.3.46).
Обозначим:
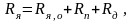
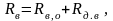
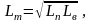
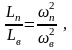
где Rя,о , Rв,о – собственные сопротивления обмотки якоря и ОНВ,
Rп – собственное сопротивление ОПВ,
Lп , Lв – индуктивности обмоток ОПВ и ОНВ,
п , в – число витков обмоток ОПВ и ОНВ,
Lm – взаимная индуктивность обмоток возбуждения,
Rд , Rд.в – добавочные сопротивления в якорной цепи и цепи ОНВ,
На основании рис.3.46 составляем исходные уравнения:
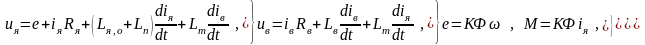
к которым добавляем основное уравнение движения электропривода
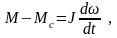
принимая статический момент Мс и суммарный момент инерции электропривода постоянными. Дифференциальные уравнения преобразуем к форме Коши:
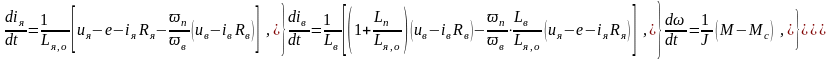
Полученная математическая модель ДПТ СВ нелинейная из-за наличия произведения переменных iя , Ф и переменных коэффициентов Lв , Lп и Lф , которые следует корректировать в соответствии с рассчитанными заранее в статическом режиме функциями:
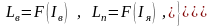
где 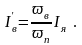
Эта модель может быть использована при моделировании электропривода с ДПТ СВ.
49. Статические характеристики дпт св
Статические характеристики ДПТ СВ при кусочно-линейной аппроксимации кривой намагничивания.
В статическом режиме (р=0)
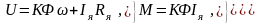 (3.164)
(3.164)
откуда находим общие выражения статических электромеханической
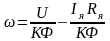 (3.165)
(3.165)
и механической
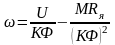 (3.166)
(3.166)
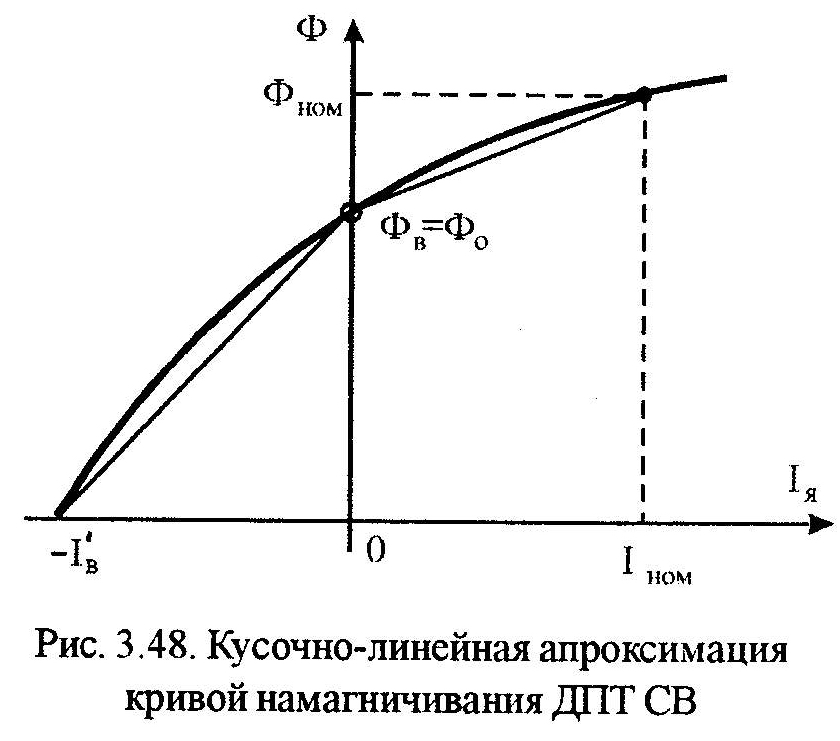
характеристик. Зависимость магнитного потока Ф от тока якоря Iя показана на рис.3.48.
Двигатели смешанного возбуждения могут быть изготовлены с любым соотношением МДС ОНВ и ОПВ. В большинстве случаев используют соотношение
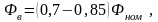 (3.167)
(3.167)
поэтому скорость идеального холостого хода двигателя
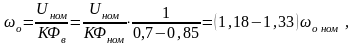 (3.168)
(3.168)
где
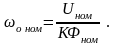 (3.169)
(3.169)
Для выявления главных свойств ДПТ СВ аппроксимируем кривую намагничивания рис.3.48 двумя отрезками:
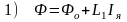 при
при
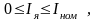 (3.170)
(3.170)
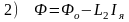 при
при
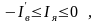 (3.171)
(3.171)
где 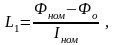 (3.172)
(3.172)
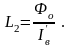 (3.173)
(3.173)
Рассмотрим
характеристики ДПТ СВ при работе в
первом квадранте и
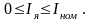 Обозначим:
Обозначим:
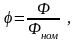 (3.174)
(3.174)
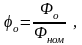 (3.175)
(3.175)
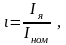 (3.176)
(3.176)
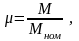 (3.177)
(3.177)
тогда получаем
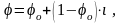 (3.178)
(3.178)
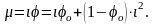 (3.179)
(3.179)
Приняв U=Uном в (3.165), после преобразований с использованием (3.174) – (3.179) найдем выражение безразмерной электромеханической характеристики ДПТ СВ на интервале 0 1:
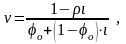 (3.180)
(3.180)
где 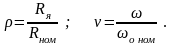
Из (3.179) находим выражение для тока якоря
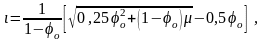 (3.181)
(3.181)
подставив которое в (3.180), получаем выражение безразмерной механической характеристики ДПТ СВ на интервале 0 1:
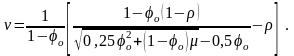 (3.182)
(3.182)
Анализ (3.182) показывает, что с увеличением скорости жесткость механической характеристики уменьшается.
Теперь
рассмотрим интервал тока якоря
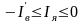 .
На этом интервале, исходя из (3.171) и
принятых выше обозначений безразмерных
величин, имеем
.
На этом интервале, исходя из (3.171) и
принятых выше обозначений безразмерных
величин, имеем
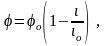 (3.183)
(3.183)
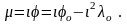 (3.184)
(3.184)
где 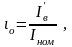 (3.185)
(3.185)
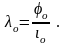 (3.186)
(3.186)
Находим ток m , при котором момент во втором квадранте достигает максимального значения m . Для этого решаем уравнение
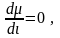
т.е. 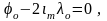
откуда
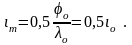 (3.187)
(3.187)
Подставляем (3.187) в (3.183) и определяем максимальный момент
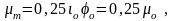 (3.188)
(3.188)
где
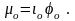 (3.189)
(3.189)
Решая (3.184) относительно тока , с учетом (3.187) получаем
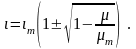 (3.190)
(3.190)
Электромеханическая безразмерная характеристика ДПТ СВ при отрицательном токе якоря (Iя<0) получается из (3.165):
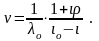 (3.191)
(3.191)
Скорость m , при которой достигается максимальный момент m , находим подстановкой (3.187) в (3.191):
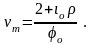 (3.192)
(3.192)
Безразмерную механическую характеристику ДПТ СВ во втором квадранте получаем при подстановке (3.190) в (3.191):
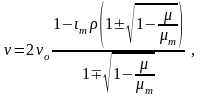 (3.193)
(3.193)
где 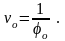
Графики электромеханической и механической характеристик ДПТ СВ показаны на рис.3.49.