
- •1.Классфификация кинематических цепей
- •2.Виды нагрузок электропривода и их классификация
- •3. Обобщенные математические модели механической части эп
- •Математическая модель и структурная схема двухмассовой модели эп.
- •5.Передаточные функции двухмассовой модели
- •6.Динамические свойства двухмассовой модели эп
- •7 .Модель,структурная схема и уравннеие движения одномассовой системы эп
- •9 .. Приведение сил, моментов сопротивления, моментов инерции и масс к валу эд для линейных пм
- •10.Приведение сил, моментов сопротивления, моментов инерции и масс к валу эд для нелинейных пм
- •13 Учет потерь в передаче.
- •14. Уточненный метод учета потерь в передаче.
- •11 Оптимальное передаточное число редуктора
- •По минимуму времени переходного процесса:
- •12Оптимальное передаточное числопо критерию минимум габарита эд
- •15. Статическая устойчивость работы эп
- •16.Механические переходные процессы эп при линейном динамическом моменте
- •18.Электромеханическая постоянная времени
- •20.Угол поворота вала электродвигателя за время переходного процесса.
- •21. Механические переходные процессы эп при нелинейном динамическом моменте
- •Теперь получаем дифференциальное уравнение:
- •С учетом (1.357) это уравнение принимает вид
- •При отсутствии диссипативных сил на основании (1.385) получаем
- •25.Уравнения напряжений, потокосцеплений и электромагнитного момента оэм.
- •26.Электромеханическая связь в эп
- •30. Модель оэм в осях u-V и её уравнения напряжений,потокосцепдений
- •31.Выражения электромагнитного момента оэм через скалярные величины и пространственные векторы.
- •33. Эквивалентная схема оэм в осях X-y для установившегося режима работы
- •Поскольку
- •34. Фазные преобразования переменных
- •Для трехфазной трехпроводной системы
- •35. Инвариантность мощности в преобразованиях уравнений оэм от осей к осям u-V
- •36 Режимы работы электродвигателей и ограничения на электромеханические преобразования энергии
- •37. Модель дпт нв в осях и её уравнения
- •38. Математическая модель дпт нв и структурная схема дпт нв в осях
- •40. Статические характеристики дпт нв
- •43 Математическая модель дпт пв в осях α–β.
- •44.Структурная схема линеаризованной модели дпт пв
- •45.Статические характеристики дпт пв при ненасыщенной магнитной системе.
- •47. Тормозные режимы работы дпт пв
- •48. Математическая модель дпт св в осях а-в
- •49. Статические характеристики дпт св
- •52. Статические характеристики ад. Механическая хар-ка и полная механическая мощность ад.
- •54. Влияние параметров на свойство и механическую характеристику ад
- •53. Электромеханические характеристики ад.
- •55. Характеристики и свойства асинхронного двигателя при питании от источника тока.
- •56.. Структурная схема линеаризованного ад при питании от источника напряжения.
- •58. Тормозные режимы ад: рекуперативное торможение и торможение противовключением
- •57.. Динамическое торможение ад при независимом возбуждении.
- •39.Уравнения , электромеханические и механические характеристики дпт нв при постоянном магнитном потоке. Структурная схема дпт нв
- •1. 1.Классфификация кинематических цепей 1
25.Уравнения напряжений, потокосцеплений и электромагнитного момента оэм.
Для четырех обмоток ОЭМ запишем уравнения электрического равновесия, т. е. уравнения Кирхгофа, используя потокосцепления обмоток:

где R1, R2 – активное сопротивление одной фазы статора и активное сопротивление одной фазы ротора,
1 , 1 , 2d , 2q – потокосцепления, соответствующие индексам обмоток.
Потокосцепления обмоток определяются результирующим действием токов всех обмоток ОЭМ:
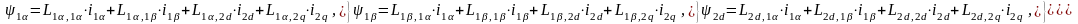
где L1,1 , L1,1 - собственные индуктивности обмоток статора,
L2d,2d , L2q ,2q - собственные индуктивности обмоток ротора,
L1,1 , L1,1 , L1,2q , L2q ,1 , L1,2d , L2d ,1 , L1,2d , L2d ,1 , L1,2q , L2q ,1 , L2d,2q , L2q ,2d – взаимные индуктивности.
Электромагнитный момент ОЭМ определяется выражением
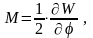
где W – электромагнитная энергия ОЭМ,
-
механический угол поворота ротора,
который связан с электрическим углом
эл
соотношением
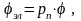
pп – число пар полюсов ОЭМ.
Теперь
получаем
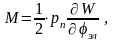
В
матричной форме электромагнитную
энергию ОЭМ можно представить как
скалярное произведение векторов
потокосцепления
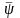 и тока
и тока
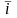 ,
т.е.
,
т.е.
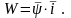 (2.21)
(2.21)
Определим вектор потокосцепления , используя матрицу (2.13):
(2.22)
Таким образом, электромагнитная энергия ОЭМ может быть записана в виде:
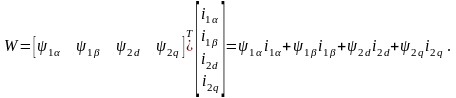 (2.23)
(2.23)
после преобразований получим
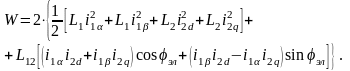 (2.24)
(2.24)
Взяв частную производную по углу эл от (2.24) и подставив в (2.20), получим окончательное выражение электромагнитного момента ОЭМ:
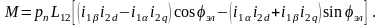 (2.25)
(2.25)
Формула (2.25) дает мгновенное значение электромагнитного момента. Она показывает, что электромагнитный момент ОЭМ является функцией электрических переменных, т. е. токов, и механической переменной – угла поворота ротора, выраженного в электрических угловых величинах.
26.Электромеханическая связь в эп
Преобразуем уравнение (2.14) в соответствии с правилами дифференцирования
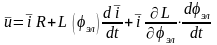 .
Так как
.
Так как
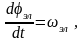 то
то
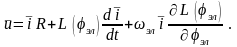 (2,28)
(2,28)
Первая составляющая в (2.28), в соответствии с законом Ома, является падением напряжения на активном сопротивлении. Вторая составляющая обусловлена изменением тока в обмотках и называется трансформаторной ЭДС. Она включает ЭДС само- и взаимоиндукции. Третья составляющая появляется из-за вращения ротора относительно статора. Она зависит от угловой скорости ротора эл и тока в обмотках. Она называется ЭДС вращения. В общем случае
ее называют ЭДС движения.
ЭДС вращения непосредственно связана с преобразованием электрической энергии в механическую.
Приведенное разложение вектора напряжения на составляющие позволяет показать взаимное влияние между электрической и механической частями ОЭМ. Как можно видеть из (2.28), любое изменение механической величины (эл = pп) приводит к изменению электрической величины – ЭДС вращения. Следовательно, при постоянной величине вектора напряжения изменяется величина вектора тока. С другой стороны, изменение электрической величины – вектора тока влечет за собой изменение электромагнитного момента и, как следствие, механической величины – угловой скорости . В этом и состоит сущность электромеханической связи в электроприводе.
Следует заметить, что трансформаторная ЭДС максимальна, когда ЭДС вращения равна нулю и наоборот.
Электрическая мощность, связанная с ЭДС вращения, разделяется на две равные части: одна из них увеличивает или уменьшает запасенную энергию, а вторая преобразуется в механическую энергию. Покажем, что это действительно так, вычислив суммарную электромагнитную мощность:
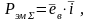
Где
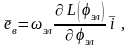
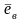 -
вектор ЭДС вращения.
-
вектор ЭДС вращения.
В связи с этим различают: статические электромеханические
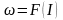 (2.38)
и механические
(2.38)
и механические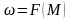 (2.39)
(2.39)
характеристики и динамические электромеханические
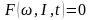 (2.40) и механические
(2.40) и механические
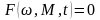 (2.41)
(2.41)
27-28.ПРЯМЫЕ И ОБРАТНЫЕ ПРЕОБРАЗОВАНИЯ ПЕРЕМЕННЫХ ДЛЯ СТАТОРА И РОТОРА ОЭМ
П реобразование,
с помощью которого координаты точки А
в новой системы координат
реобразование,
с помощью которого координаты точки А
в новой системы координат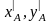 выражаются через координаты xА,yА
этой точки в старой системе координат,
называется прямым координатным
преобразованием. Из геометрических
построений на Рис. 2.3 следует, что
выражаются через координаты xА,yА
этой точки в старой системе координат,
называется прямым координатным
преобразованием. Из геометрических
построений на Рис. 2.3 следует, что
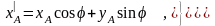
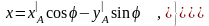
Под
вектором
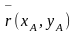 будем понимать вектор
будем понимать вектор
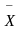 любой переменной ОЭМ, например, вектор
напряжения
любой переменной ОЭМ, например, вектор
напряжения
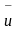 ,
вектор тока
,
вектор тока
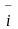 ,
вектор потокосцепления
,
вектор потокосцепления
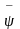 .
Под координатными осями будем понимать:
.
Под координатными осями будем понимать:
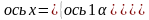

где оси u, вращаются с постоянной угловой скоростью К относительно неподвижных осей 1-1.
Угол поворота осей u, относительно неподвижных осей 1-1 равен
К=К t (2.48)
где t – время.
Теперь,
после оговоренных условий, можем записать
уравнения координатных преобразований
для вектора
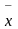 любой переменной ОЭМ:
любой переменной ОЭМ:
Прямые преобразования:
а) для переменных статора: б) для переменных ротора:
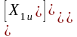 (2.49)
(2.49)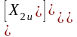 (2.50)
(2.50)
Обратные преобразования: б) для переменных ротора:
а) для переменных статора:
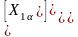
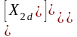
(2.51) (2.52)
где 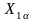 ,
,
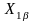 – проекции вектора
– проекции вектора
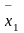 на оси координат 1-1
,
на оси координат 1-1
,
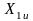 ,
,
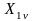 – проекции вектора
на оси координат 1u-1
,
– проекции вектора
на оси координат 1u-1
,
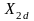 ,
,
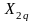 – проекции вектора
– проекции вектора
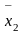 на оси координат 2d-2q,
на оси координат 2d-2q,
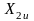 ,
,
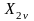 – проекции вектора
на оси координат 2u-2
.
– проекции вектора
на оси координат 2u-2
.
Для упрощения дальнейших записей обозначим:
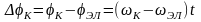 ,(2.53);
,(2.53);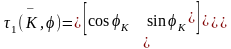 ,(2.54)
,(2.54)
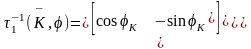 ,(2.55);
,(2.55);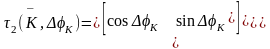 ,(2.56)
,(2.56)
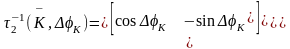 ,(2.57)
,(2.57)
где 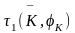 – матрица поворота осей координат
статора,
– матрица поворота осей координат
статора,
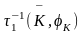 – обратная матрица поворота осей
статора,
– обратная матрица поворота осей
статора,
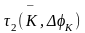 – матрица поворота
осей координат ротора,
– матрица поворота
осей координат ротора,
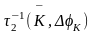 – обратная матрица
поворота осей координат ротора,
– обратная матрица
поворота осей координат ротора,
Можно видеть, что
=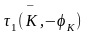 =
=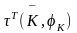 ,
,
=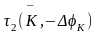 =
=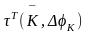 ,
,
т. е. обратные матрицы поворота равны транспонированным матрицам. После введения этих обозначений можем записать:
Прямые преобразования: Обратные преобразования:
а) для переменных статора: а) для переменных статора:
(2.58) (2.60)
б) для переменных ротора: б) для переменных ротора: (2.59) (2.61)
