
6.Законы алгебры логики
На основе рассмотренных выше аксиом, выводятся теоремы, содержащие основные законы АЛ:1.Закон нулевого множества:
0 v x = x; 0 & x = 0; 0 & x1 & x2 &... & xn &... = 0. |
2.Закон универсального множества:
|
3.Закон повторения: x & x = x; x v x = x.
4.Закон двойной инверсии: х = х5.Законы дополнительности: а) исключенного третьего x v x = 1.б) логическое противоречие x & x = 0.6.Коммутативный (переместительный) закон: x & y = y & x; x v y = y v x.7.Ассоциативный (сочетательный) закон:
x&(y&z) = (x&y)&z = x&y&z; x v (yvz) = (xvy) v z = x v y v z. |
8.Дистрибутивный (распределительный) закон: x&(y v z) = x&y v x&z;
x v y&z = (x v y)&(x v z).9Законы поглощения:
x & (x v y) = x; x v x&y = x. x & (x v y) = x & y; x v x&y = x v y. |
10.Законы склеивания: а) полного(x v y)&(x v y) = x.б) неполного x&y v x&y = x v x&y v x&y;
(xvy)&(xvy) = x&(x v y)&(x v y). |
11.Законы инверсии (теоремы де Моргана):
x1&x2&... &xn = x1vx2v..vxn; |
|
x1vx2v... vxn = x1&x2&...&xn. |
|
12.Теоремы разложения (декомпозиции ЛФ):
f (x,y,...,z) = x& f (1,y,...,z) v x& f (0,y,...,z);
f (x,y,...,z) = (xv f (0,y,...,z))&(xv f (1,y,...,z)).
13.Следствия из теорем разложения:
x & f (x,y,..,z) = x & f (1,y,..,z); |
x v f (x,y,..,z) = x v f (0,y,..,z); |
x & f (x,y,..,z) = x & f (0,y,..,z); |
x v f (x,y,..,z) = x v f (1,y,..,z). |
14.Теорема Шеннона (обобщение теорем де Моргана):
f (x,y,...,z,&,v)=f (x,y,...,z,v,&). |
|
Данная теорема утверждает, что инверсия любой функции в АЛ получается путем замены каждой переменной ее инверсией и одновременно взаимной заменой символов конъюнкции и дизъюнкции.
Справедливость любого закона АЛ можно доказать разными методами. Законы (1-5) доказываются путем прямой подстановки вместо переменной значений 0 и 1. Ряд законов доказывается методом перебора всех возможных значений переменных, для которых проверяется справедливость закона. Для доказательства закона достаточно показать тождественность выражений, образующих левую и правую стороны доказываемого соотношения при всех наборах переменных, принимающих значения 0 или 1. Общий формальный метод доказательства законов АЛ состоит в том, что справедливость каждого закона доказывается на основе аксиом и ранее доказанных законов. Доказательство заключается в приведении обеих частей выражения к одному виду с помощью последовательных преобразований. Для доказательства законов инверсии следует воспользоваться методом математической индукции.
7.Функционально-полные базисы (ФПБ)Система булевых функций W называется функционально-полной, если произвольная булева функция вида f (x1, x2, ..., xn) может быть представлена суперпозицией функций x1, x2, ... ,xn и суперпозицией конечного числа функций системы W.В качестве простейших принято рассматривать следующие пять базисов:1Дизъюнкция (xivxj), конъюнкция (xi&xj), инверсия (xi); 2.Дизъюнкция (xivxj), инверсия (xi); 3.Конъюнкция (xi&xj), инверсия (xi); 4.Стрелка Пирса (xi xj = Xi V Xj); 5.Штрих Шеффера (xi | xj = Xi & Xj). С точки зрения практической реализации булевых функций функциональная полнота базисов (1-5) показывает, что произвольная логическая сеть может быть построена из простых функциональных элементов, вплоть до случая элементов одного типа (например, Пирса или Шеффера).В действительности электронной промышленностью выпускается ограниченный, но заведомо избыточный набор логических элементов, что позволяет сократить общее число микросхем в конкретном логическом блоке за счет расширения номенклатуры.
|
|
11.Аналитическое
представление булевой функции.
Рассмотрим
булеву функцию f
(X1,
X2,
..., Xn);
каждому набору входных переменных (X1,
X2,
..., Xn)
можно сопоставить двоичное число вида:i
= X1·
2n-1
+ X2·
2n-2
+ ... + Xn·
20.Можно
ввести функцию Fi(X1,
X2,
..., Xn)
следующим образом:Fi
= {0;1},1 – если номер набора есть;0 – в
противном случае.Тогда заданную функцией
алгебры логики можно представить в
форме:Fi(X1,
X2,
..., Xn)
= Fi1
v Fi2
v ... v Fik
= v Fij,
ij Т,где
Т есть множество наборов, на которых
функция принимает истинное значение
("1").В инженерной практике номера
наборов i записывают десятичными числами
и функцию задают в виде:F = v (j1,
j2,
..., jn)
=
![]() (j1,
j2,
..., jn)Для
примера(в столбик) X1
00001111 X2
001100 X3
01010101
f
00010111
получим:F(X1,
X2,
..., Xn)
= 1011
v
1101
v
1110
v
1111F
= v
(3, 5, 6, 7) =
(3,
5, 6, 7)Множество Т = (3, 5, 6, 7)Доказано, что
функцию Fi
можно представить как конъюнкцию
аргументов (X1,
X2,
..., Xn),
такую, что если Xi
в наборе (X1,
X2,
..., Xn)
равен 0, то в конъюнкцию входит инверсия
Xi
(т.е. Xi),
если Xi
равен 1, то в конъюнкцию входит Xi.
(j1,
j2,
..., jn)Для
примера(в столбик) X1
00001111 X2
001100 X3
01010101
f
00010111
получим:F(X1,
X2,
..., Xn)
= 1011
v
1101
v
1110
v
1111F
= v
(3, 5, 6, 7) =
(3,
5, 6, 7)Множество Т = (3, 5, 6, 7)Доказано, что
функцию Fi
можно представить как конъюнкцию
аргументов (X1,
X2,
..., Xn),
такую, что если Xi
в наборе (X1,
X2,
..., Xn)
равен 0, то в конъюнкцию входит инверсия
Xi
(т.е. Xi),
если Xi
равен 1, то в конъюнкцию входит Xi.
12.Графическое
представление булевой функции. Карты
карно.графическое
представление мат объектов является
наиболее наглядным и удобным для
конструкт использования. Поэтому
широкое применение находит представление
булевых функций с помощью пространственных
двоичных решёток.Поскольку одна булева
переменная может принимать два значения
"0" и "1", то её можно
интерпретировать отрезком прямой,
являющимся одномерным пространством.![]() От
одной переменной может быть построено
четыре функции в ал. Их можно представить
на этом отрезке, показывая нулевое
значение функции как "0", а единичное
- как "1" .
От
одной переменной может быть построено
четыре функции в ал. Их можно представить
на этом отрезке, показывая нулевое
значение функции как "0", а единичное
- как "1" .
|
|
|||
x |
g1 |
g2 |
g3 |
g4 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
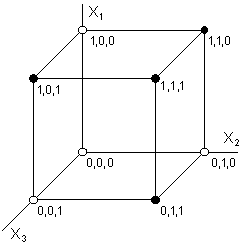

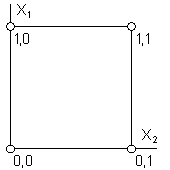 Для
двух и трех переменных мы получим
квадрат на плоскости и куб в трёхмерном
пространстве соответственно.Для нашего
примера:f
(X1,X2,X3)
= X1·
X2·
X3v
X1·
X2·
X3v
X1·
X2·
X3v
X1·
X2·
X3.любая
таблично заданная функция алгебры
логики может быть представлена в
форме:Фi(X1,
X2,
..., Xn)
= Фi1·
Фi2·
... Фik
= &Фij,
ij Т0,где
Фi(X1,
X2,
..., Xn)
- характеристическая функция нуля,
определённая как:Фi
= {0;1}0 – если номер набора есть i,1 – в
противном случае.Т0
– есть множество наборов, из которых
функция обращается в ноль.
Для
двух и трех переменных мы получим
квадрат на плоскости и куб в трёхмерном
пространстве соответственно.Для нашего
примера:f
(X1,X2,X3)
= X1·
X2·
X3v
X1·
X2·
X3v
X1·
X2·
X3v
X1·
X2·
X3.любая
таблично заданная функция алгебры
логики может быть представлена в
форме:Фi(X1,
X2,
..., Xn)
= Фi1·
Фi2·
... Фik
= &Фij,
ij Т0,где
Фi(X1,
X2,
..., Xn)
- характеристическая функция нуля,
определённая как:Фi
= {0;1}0 – если номер набора есть i,1 – в
противном случае.Т0
– есть множество наборов, из которых
функция обращается в ноль.
8.Формы представления логических функций. Аналитическое представление.Рассмотрим булеву функцию f (X1, X2, ..., Xn); каждому набору входных переменных (X1, X2, ..., Xn) можно сопоставить двоичное число вида: i = X1· 2n-1 + X2· 2n-2 + ... + Xn· 20.Можно ввести функцию Fi(X1, X2, ..., Xn) следующим образом: Fi = {0;1}, 1 – если номер набора есть; 0 – в противном случае.Тогда заданную функцией алгебры логики можно представить в форме: Fi(X1, X2, ..., Xn) = Fi1 v Fi2 v ... v Fik = v Fij, ij Т, где Т есть множество наборов, на которых функция принимает истинное значение ("1").Графическое представление математических объектов является наиболее наглядным и удобным для конструктивного использования. Поэтому широкое применение находит представление булевых функций с помощью пространственных двоичных решёток.Одна булева переменная может принимать два значения "0" и "1", то её можно интерпретировать отрезком прямой, являющимся одномерным пространством. Для двух и трех переменных мы получим квадрат на плоскости и куб в трёхмерном пространстве.
10.Карты
Карно.Нормальные формы булевых
функцийКарта
Карно
– это
двумерная табличная форма представления
булевой функции, позволяющая
в наглядной графической форме легко
отыскать минимальные ДНФ логических
функций. Каждой клетке в таблице
сопоставляется дизъюнкт СДНФ
минимизируемой
функции, причем так, что любым осям
симметрии таблицы соответствуют
зоны, взаимно инверсные по какой-либо
переменной.расположение
клеток позволяет легко определить
склеивающиеся термы СДНФ (отличающиеся
знаком инверсии только одной переменной):
они располагаются в таблице симметрично.
Например,
следующая карта Карно построена для
импликации двух переменных х
у.
В ячейки карты вписываются значения
из таблицы истинности функции, при
этом, если перед соответствующей
переменной стоит знак отрицания, то в
таблице истинности выбирается строка
с ложным значением данной переменной,
иначе – с истинным значением. Единичные
значения функции показывают те
дизъюнкты, которые присутствуют в СДНФ
этой функции. Расположения элементов
в картах Карно функции 2 переменных-в
один конъюнкт эта переменная входит
без отрицания, а в другой – с
отрицанием. Алгоритм поиска минимальной
ДНФ по карте Карно основан на выявлении
на карте мин кол-ва макс квадратов или
прямоугольников со сторонами, равными
степени двойки, так, чтобы они состояли
только из ячеек, содержащих единицы.
Нормальные
формы. Произведение
Единичные
значения функции показывают те
дизъюнкты, которые присутствуют в СДНФ
этой функции. Расположения элементов
в картах Карно функции 2 переменных-в
один конъюнкт эта переменная входит
без отрицания, а в другой – с
отрицанием. Алгоритм поиска минимальной
ДНФ по карте Карно основан на выявлении
на карте мин кол-ва макс квадратов или
прямоугольников со сторонами, равными
степени двойки, так, чтобы они состояли
только из ячеек, содержащих единицы.
Нормальные
формы. Произведение![]() называется
элементарной
конъюнкцией
ранга k, если все переменные в нем
различны. Логическая единица считается
элементарной конъюнкцией ранга 0.
Логическая сумма
называется
элементарной
конъюнкцией
ранга k, если все переменные в нем
различны. Логическая единица считается
элементарной конъюнкцией ранга 0.
Логическая сумма![]() называется
элементарной
дизъюнкцией
ранга r, если все переменные в ней
различны. Логический ноль считается
элементарной дизъюнкцией ранга 0.Формула
вида u1
v
u2
v
... v
ui
где: u1,
u2,
... ui
– различные элементарные конъюнкции
рангов r1,
r2,
... ri
соответственно называется дизъюнктивной
нормальной формой
(ДНФ), а число
называется
элементарной
дизъюнкцией
ранга r, если все переменные в ней
различны. Логический ноль считается
элементарной дизъюнкцией ранга 0.Формула
вида u1
v
u2
v
... v
ui
где: u1,
u2,
... ui
– различные элементарные конъюнкции
рангов r1,
r2,
... ri
соответственно называется дизъюнктивной
нормальной формой
(ДНФ), а число
![]() –
сложностью
ДНФ.
Формула вида S1·
S2·
... · St
где:
S1,
S2,
... St
– различные элементарные дизъюнкции
рангов p1,
p2,
... pt
соответственно называется конъюнктивной
нормальной формой
(КНФ), а число
–
сложностью
ДНФ.
Формула вида S1·
S2·
... · St
где:
S1,
S2,
... St
– различные элементарные дизъюнкции
рангов p1,
p2,
... pt
соответственно называется конъюнктивной
нормальной формой
(КНФ), а число
![]() –
сложностью
КНФ.Всякая
булева функция, отличная от тождественного
"0" может быть задана ДНФ и, в общем
случае, неоднозначно. Аналогичное
правило действует и для КНФ, если булева
функция не тождественна "1".По
таблице задающей булеву функцию f
(Х1,
Х2,
... Хn)
строится совершенная
ДНФ:
u1
v
u2
v
... v
uS,
где
–
сложностью
КНФ.Всякая
булева функция, отличная от тождественного
"0" может быть задана ДНФ и, в общем
случае, неоднозначно. Аналогичное
правило действует и для КНФ, если булева
функция не тождественна "1".По
таблице задающей булеву функцию f
(Х1,
Х2,
... Хn)
строится совершенная
ДНФ:
u1
v
u2
v
... v
uS,
где
![]() таковы,
что i = 1, 2, ..., S и наборы i1,
i2,
..., in
таковы, что f
(i1,
i2,
..., in)
= 1.Совершенная
КНФ
имеет вид:
S1
& S2
& ... & SC
где
таковы,
что i = 1, 2, ..., S и наборы i1,
i2,
..., in
таковы, что f
(i1,
i2,
..., in)
= 1.Совершенная
КНФ
имеет вид:
S1
& S2
& ... & SC
где
![]() таковы,
что i
= 1, 2, ..., S
и наборы i1,
i2,
..., in
таковы, что f
(i1,
i2,
..., in)
= 0.Совершенная ДНФ и КНФ для заданной
булевой функции строятся однозначно.
Они четко получаются из таблицы
истинности булевой функции следующим
образом.Для
СДНФ:1необходимо
выбрать из таблицы истинности функции
все наборы аргументов, на которых
функция принимает значения "1";
2.выписать
элементарные конъюнкции, соответствующие
этим наборам элементов; если Хi
входит в данный набор как 1, он вписывается
без изменения в конъюнкцию, если Хi
входит в данный набор как 0, то в конъюнкции
вписывается отрицание Хi
(т.е. Xi);
3.все
полученные элементарные конъюнкции
соединяются между собой знаками
дизъюнкции (т.е. v).
Для
СКНФ:1.необходимо
выбрать в таблице истинности функции
все наборы аргументов, на которых
функция принимает значения "0";
2.выписать
элементарные дизъюнкции, соответствующие
этим наборам элементов; если Xi
входит в данный набор как 0, он вписывается
без изменений в дизъюнкцию, если Xi
входит в данный набор как 1, то в дизъюнкцию
вписывается его отрицание (т.е. Xi);
3.все
полученные элементарные дизъюнкции
соединяются между собой знаками
конъюкции .
таковы,
что i
= 1, 2, ..., S
и наборы i1,
i2,
..., in
таковы, что f
(i1,
i2,
..., in)
= 0.Совершенная ДНФ и КНФ для заданной
булевой функции строятся однозначно.
Они четко получаются из таблицы
истинности булевой функции следующим
образом.Для
СДНФ:1необходимо
выбрать из таблицы истинности функции
все наборы аргументов, на которых
функция принимает значения "1";
2.выписать
элементарные конъюнкции, соответствующие
этим наборам элементов; если Хi
входит в данный набор как 1, он вписывается
без изменения в конъюнкцию, если Хi
входит в данный набор как 0, то в конъюнкции
вписывается отрицание Хi
(т.е. Xi);
3.все
полученные элементарные конъюнкции
соединяются между собой знаками
дизъюнкции (т.е. v).
Для
СКНФ:1.необходимо
выбрать в таблице истинности функции
все наборы аргументов, на которых
функция принимает значения "0";
2.выписать
элементарные дизъюнкции, соответствующие
этим наборам элементов; если Xi
входит в данный набор как 0, он вписывается
без изменений в дизъюнкцию, если Xi
входит в данный набор как 1, то в дизъюнкцию
вписывается его отрицание (т.е. Xi);
3.все
полученные элементарные дизъюнкции
соединяются между собой знаками
конъюкции .
13)Двойственность
булевых функций.Операция
(или функция) f
называется двойственной
д\ операции, если табл, задающ ф-ю f,
получается из табл, задающей ф-ю, путём
замены в ней всюду "0" на "1" и
"1" на "0", включая и замену
значений функции.Прим:рассмотрим
ф-и дизъюн и коньюк 2 перем, кот задаются
соответствующ табл(в
столбик)Х10011
Х20101
V0111;
X10011
X20101
&
0001Преобразуем
вторую таблицу в соответствии с введенным
обозначением, получим:X1
1100X21010
?1110
Х10011
Х20101
V0111Что
соответствует таблице операции
дизъюнкции с точностью до перестановки
строк.Преобразование формул, при котором
знаки всех операций в логическом
выражении заменяются на знаки двойственных
им операций, "0" заменяется на "1",
а "1" на "0", называется
преобразованием двойственности.прим
рассмотрим преобразование следующей
функции3переменных(табл3перем).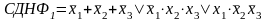
 Выполним
из функции преобразование
двойственности(Табл.Х111110000Х211001100Х310101010f01100111)Совершенные
нормальные формы для двойственной
функции f
*
примут вид:
Выполним
из функции преобразование
двойственности(Табл.Х111110000Х211001100Х310101010f01100111)Совершенные
нормальные формы для двойственной
функции f
*
примут вид:


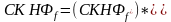


14)Минимиз
лог ф-й: общее представление.Задача
минимиз булевых функций возникает из
практич потребностей построения лог
схем, различающих аналитич выражения
бул функций.Первич аналитич формой,
получаемой из таблич предст-я лог ф-и
явл СДНФ или СКНФ. В бол-ве случаев знач
ф-и в виде СДНФ и СКНФ явл заведомо не
экономной, избыточ и м\б построена
эквивал ф-я, реализующая в своем
представлении меньшее число перем и
операций.Сложностью нормальной формы
следует понимать сумму рангов её
составляющих, т.е. число букв в ней.
=>ДНФ, имеющая наим сумму рангов среди
всех ДНФ, эквивалентных данной функции,
назыв-ся мин ДНФ (МДНФ). ДНФ, имеющая
наим длину среди всех ДНФ, эквивал
данной ф-и называется кратчайшей ДНФ
(КДНФ).Тупиковая ДНФ-
ДНФ,
при удалении из которой любой коньюкции,
полученная в результате ДНФ не будет
эквивалентна исходной.Способы
минимизации:1Граф
способ минимиз (к Карно)Граф
способ реализ Бул ф-й карт Карно
представляет собой операции склеив и
поглощ.Карты Карно рассм-ся как
перестроенные сооответств-им образом
табл.истинности функций. Можно
рассматривать как 3х
мерную развертку булевого куба. Основным
методом минимизации лог
ф-и представленных в СДНФ,СКНФ явл оп-и
попар склеив(м\у 2 термами или членами,
содержащ одинаковые переменные) неполн
и элемент п Н-р,1)
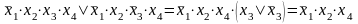 2)
2)
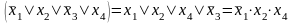
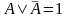
 главной
задачей минимизации при СКНФ и СДНФ
является поиск термов пригодных к
склейке с последующ. поглощением. Карта
Карно м.б. составлена для любого числа
переменных.После того как карта заполнена
можно приступать к минимиз, если
необходимо получить МДНФ,то в карте
рассм-ся только клетки, к-ые содержат
единицы; если МКНФ-клетки, где содержатся
нули.Минимизация
провод-ся по след-им правилам(для
ДНФ)1.Объед-т
смежн клетки содерж 1 в область так,
чтобы одна область содержала 2n
клеток.2.Область д\распол-ся симм оси.
Оси располагаются через каждые 4
клетки.3. Не смеж области расп-ся симм
относ осей они м\объед-ся в одну.4.Область
д.б. как можно больше,а кол-во областей
меньше.5. Обл-ти могут пересекаться.Далее
выбирается 1ая обл-ть для перем не меняющ
значение в этой обл-ти. Выпис-ся конъюнкц,
е.неменяющ перем нулевая над ней ставят
инверсию.Далее выполняется аналог
операция для всех областей , после этого
конъюнкции обла объед-ся в дизъюнкц.ДляКНФ:
рассм-ся клетки с нулями ,неменяющ перем
в пределах одной обл объед-ся в
дизъюнкции.Дизъюнкции областей объед-ся
в конъюн-ции, но при этом минимиз
считается законченной.
главной
задачей минимизации при СКНФ и СДНФ
является поиск термов пригодных к
склейке с последующ. поглощением. Карта
Карно м.б. составлена для любого числа
переменных.После того как карта заполнена
можно приступать к минимиз, если
необходимо получить МДНФ,то в карте
рассм-ся только клетки, к-ые содержат
единицы; если МКНФ-клетки, где содержатся
нули.Минимизация
провод-ся по след-им правилам(для
ДНФ)1.Объед-т
смежн клетки содерж 1 в область так,
чтобы одна область содержала 2n
клеток.2.Область д\распол-ся симм оси.
Оси располагаются через каждые 4
клетки.3. Не смеж области расп-ся симм
относ осей они м\объед-ся в одну.4.Область
д.б. как можно больше,а кол-во областей
меньше.5. Обл-ти могут пересекаться.Далее
выбирается 1ая обл-ть для перем не меняющ
значение в этой обл-ти. Выпис-ся конъюнкц,
е.неменяющ перем нулевая над ней ставят
инверсию.Далее выполняется аналог
операция для всех областей , после этого
конъюнкции обла объед-ся в дизъюнкц.ДляКНФ:
рассм-ся клетки с нулями ,неменяющ перем
в пределах одной обл объед-ся в
дизъюнкции.Дизъюнкции областей объед-ся
в конъюн-ции, но при этом минимиз
считается законченной.
15)Постановка
задачи минимиз лог ф-й.Задача
минимиз бул ф-й возникает из практич
потребн построения лог схем, различающ
аналитич выражения бул ф-й.Первичн
аналит формой, получ из табличн представ-я
лог ф-и явл СДНФ или СКНФ.В бол-ве случаев
значение ф-и в виде СДНФ и СКНФ явл
заведомо не экономной, избыточн и м\б
построена эквивал ф-я, реализующ в своем
представлении меньшее число переменных
иопераций.Например,
 Используя
законы алгебры логики, получим:
Используя
законы алгебры логики, получим: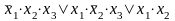 Простейш
или мин представление бул ф-и необходимо
искать в опред базисе. Наилучшие
результаты получены для базиса,
включаюшего инверсию, дизъюкцию и
коньюкцию. Поэтому в дальнейшем задача
минимизации будет рассматриваться
именно в этом базисе.В соответствии
заданным ранее определением под
сложностью нормальной формы следует
понимать сумму рангов её составляющих,
т.е. число букв в ней. Поэтому ДНФ, имеющая
наим сумму рангов среди всех ДНФ, эквивал
данной ф-и, назыв мин ДНФ (МДНФ).Если к
ДНФ примен лишь операции склеив AB
v
AB
= A
и поглощ AB
v
A = A,
то рано или поздно дальнейш преобраз
окажутся невозможн. В этом случае будет
получаться тупиковая ДНФ, т.е. такая
ДНФ, при удалении из которой любой
коньюкции, полученная в результате ДНФ
не будет эквив исходной.Разработанные
методы минимизации достаточно хорошо
работают для функций первой и третьей
группы по классификации Потёмкина и
не дают гарантированного результата
для функций второй группы.Потёмкин
предложил разделять логические функции
на три группы:функции малого числа
аргументов(ф-и 3 – 5 арг, кот часто встреч
при реализ цифр аппаратуры.); "объективные"
функции многих аргументов(ф-и >5 арг,
кот отраж некот естеств, технич или
природн зав-ти.); "субъективные"
функции многих аргументов(ф-и больш
числа арг. Д\них функций харак наличие
внут структуры и возмож-тей декомпоз
на более простые позиции).Интервалом
l-го
ранга
называется подмножество вершин двоичного
n-мерного куба, соответств элементарн
конъюнкции l-го
ранга.Покрытием
l-го
ранга
называется подмножество клеток к Карно
n-го порядка, соответствующ элементарной
конъюнкции l-го
ранга.При задании бул функции в виде
ДНФ, будет задано и мн-во ее еденичн
значений, что будет соответствовать
комбинации интервалов на пространств
кубе или комбинации покрытий на к Карно.
Простейш
или мин представление бул ф-и необходимо
искать в опред базисе. Наилучшие
результаты получены для базиса,
включаюшего инверсию, дизъюкцию и
коньюкцию. Поэтому в дальнейшем задача
минимизации будет рассматриваться
именно в этом базисе.В соответствии
заданным ранее определением под
сложностью нормальной формы следует
понимать сумму рангов её составляющих,
т.е. число букв в ней. Поэтому ДНФ, имеющая
наим сумму рангов среди всех ДНФ, эквивал
данной ф-и, назыв мин ДНФ (МДНФ).Если к
ДНФ примен лишь операции склеив AB
v
AB
= A
и поглощ AB
v
A = A,
то рано или поздно дальнейш преобраз
окажутся невозможн. В этом случае будет
получаться тупиковая ДНФ, т.е. такая
ДНФ, при удалении из которой любой
коньюкции, полученная в результате ДНФ
не будет эквив исходной.Разработанные
методы минимизации достаточно хорошо
работают для функций первой и третьей
группы по классификации Потёмкина и
не дают гарантированного результата
для функций второй группы.Потёмкин
предложил разделять логические функции
на три группы:функции малого числа
аргументов(ф-и 3 – 5 арг, кот часто встреч
при реализ цифр аппаратуры.); "объективные"
функции многих аргументов(ф-и >5 арг,
кот отраж некот естеств, технич или
природн зав-ти.); "субъективные"
функции многих аргументов(ф-и больш
числа арг. Д\них функций харак наличие
внут структуры и возмож-тей декомпоз
на более простые позиции).Интервалом
l-го
ранга
называется подмножество вершин двоичного
n-мерного куба, соответств элементарн
конъюнкции l-го
ранга.Покрытием
l-го
ранга
называется подмножество клеток к Карно
n-го порядка, соответствующ элементарной
конъюнкции l-го
ранга.При задании бул функции в виде
ДНФ, будет задано и мн-во ее еденичн
значений, что будет соответствовать
комбинации интервалов на пространств
кубе или комбинации покрытий на к Карно.
16)
Граф способ минимиз (использ к Карно).Граф
способ реализац Бул ф-й к Карно предст
собой операции 1склеив и поглощ.К Карно
рассм-ся как перестр сооответствующ
образом табл.истинности ф-й. М\рассматр
как 3х
мерную развертку бул куба. Основн
методом минимиз лог ф-и явл операции
попарн склеивания неполного и
элементарного поглощения. Опер попарн
склеив осущ м\у 2 термами или членами,
содержащ один переменные. Вхожд которых
прямые и инверсные совпадают для всех
перем кроме одной. В этом случае все
перем кроме 1 м\вынести за скобки,а
оставшиеся в скобках прямое и инверсное
вхождение1 перем подвергать склейке.
Н-р,1)
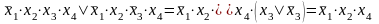 2)
Т.о.
главной задачей минимизации при СКНФ
и СДНФ является поиск терминов пригодных
к склейке с последним поглощением, что
для больших форм может оказаться
достаточно сложной задачей Булевых
функций n-переменных
представленные в виде СДНФ и СКНФ. Могут
иметь в своём составе 2n
различных термов.Все эти члены составляют
некоторую структуру топологических
эквивалентному n-мерному
кубу, причём любые 2 терма соединённые
ребром пригодны для склейки и поглощения.
(п)В случае функции 3х
переменных
приходиться иметь дело с кубом.Для
упрощения работы с булев. Функциями
большого числа переменных предложим
следующий прием: куб представляющий
собой структуру термов разворачивается
на плоскость(р)Анал-но можно работать
с ф-ями 4х
, 5ти
и более переменных.К Карно м.б. состав
д\люб числа перем. К Карно представл
собой табл. истинности составленной в
2х
мерном виде.Верхн строка к.К. явл-ся
соседней с нижней, а правый столбец
соседним слева,т.е. сворач в тор,на
пересечении строки и столбца простирается
соответствующее значение из табл.
истинности ф-ций. После того как карта
заполнена можно приступать к минимизации,
если необходимо получить МДНФ,то в
карте рассм-ся только клетки, к-ые
содержат1; если МКНФ-клетки, где
содержатся 1.Минимиз провод-ся по след-им
правилам(для ДНФ)1.Объединяет смежные
клетки содержащие единицы в область
так, чтобы одна область содержала 2n
клеток2.Область должна располагаться
симметрично оси(осей). Оси располагаются
через каждые 4 клетки.3. Не смежные
области располагаются симметрично
относительно осей(оси) они могут
объединяться в одну.4.Область д.б. как
можно больше,а кол-во областей меньше.5.
Обл-ти могут пересекаться6.Возможно
несколько вариантов покрытия. Далее
выбирается 1ая обл-ть для переменных
не меняющих своё значение в этой обл-ти.
Выпис-ся конъюнкция, если неменяющаяся
переменная нулевая над ней ставят
инверсию.Далее выполняется аналогичная
операция для всех областей , после этого
конъюнкции областей объед-ся в
дизъюнкции.ДляКНФ: рассм-ся клетки с
нулями ,неменяющиеся переменные в
пределах одной области объед-ся в
дизъюнкции.Дизъюнкции областей объед-ся
в конъюн-ции, но при этом минимизация
считается законченной.При задании бул
функции в виде ДНФ, будет задано и мн-во
ее еденичных значений, что будет
соответствовать комбинации интервалов
на пространств кубе или комбинации
покрытий на карте Карно.Задача нахождения
МДНФ может быть сформулирована как
задача построения такого множества
покрытий единичных значений булевой
функции, при котором сложность ДНФ
будет минимальной.Графически это
означает, что необходимо и достаточно
найти множество покрытий минимального
ранга, представляющих множество
единичных значений булевой функции.
2)
Т.о.
главной задачей минимизации при СКНФ
и СДНФ является поиск терминов пригодных
к склейке с последним поглощением, что
для больших форм может оказаться
достаточно сложной задачей Булевых
функций n-переменных
представленные в виде СДНФ и СКНФ. Могут
иметь в своём составе 2n
различных термов.Все эти члены составляют
некоторую структуру топологических
эквивалентному n-мерному
кубу, причём любые 2 терма соединённые
ребром пригодны для склейки и поглощения.
(п)В случае функции 3х
переменных
приходиться иметь дело с кубом.Для
упрощения работы с булев. Функциями
большого числа переменных предложим
следующий прием: куб представляющий
собой структуру термов разворачивается
на плоскость(р)Анал-но можно работать
с ф-ями 4х
, 5ти
и более переменных.К Карно м.б. состав
д\люб числа перем. К Карно представл
собой табл. истинности составленной в
2х
мерном виде.Верхн строка к.К. явл-ся
соседней с нижней, а правый столбец
соседним слева,т.е. сворач в тор,на
пересечении строки и столбца простирается
соответствующее значение из табл.
истинности ф-ций. После того как карта
заполнена можно приступать к минимизации,
если необходимо получить МДНФ,то в
карте рассм-ся только клетки, к-ые
содержат1; если МКНФ-клетки, где
содержатся 1.Минимиз провод-ся по след-им
правилам(для ДНФ)1.Объединяет смежные
клетки содержащие единицы в область
так, чтобы одна область содержала 2n
клеток2.Область должна располагаться
симметрично оси(осей). Оси располагаются
через каждые 4 клетки.3. Не смежные
области располагаются симметрично
относительно осей(оси) они могут
объединяться в одну.4.Область д.б. как
можно больше,а кол-во областей меньше.5.
Обл-ти могут пересекаться6.Возможно
несколько вариантов покрытия. Далее
выбирается 1ая обл-ть для переменных
не меняющих своё значение в этой обл-ти.
Выпис-ся конъюнкция, если неменяющаяся
переменная нулевая над ней ставят
инверсию.Далее выполняется аналогичная
операция для всех областей , после этого
конъюнкции областей объед-ся в
дизъюнкции.ДляКНФ: рассм-ся клетки с
нулями ,неменяющиеся переменные в
пределах одной области объед-ся в
дизъюнкции.Дизъюнкции областей объед-ся
в конъюн-ции, но при этом минимизация
считается законченной.При задании бул
функции в виде ДНФ, будет задано и мн-во
ее еденичных значений, что будет
соответствовать комбинации интервалов
на пространств кубе или комбинации
покрытий на карте Карно.Задача нахождения
МДНФ может быть сформулирована как
задача построения такого множества
покрытий единичных значений булевой
функции, при котором сложность ДНФ
будет минимальной.Графически это
означает, что необходимо и достаточно
найти множество покрытий минимального
ранга, представляющих множество
единичных значений булевой функции.
17)Аналитические
способы минимизации (метод Квайна).Метод
минимиз Квайна представляет собой лок
алгоритм, включающ опред послед-ть
этапов . Предполагается, что исходная
минимиз функция задач, в СДНФ.ЭТАП 1.
Нахождение первичных импликант.
Импликантой
некоторой бул ф-и назыв др бул ф-я, такая
что мн-во нул знач импликанты Nимп.(0)
пересекается со мн-вом нул знач ф-и
Nf (0),
а мн-во единичн знач Nимп.(1)
принадлежит Nf
(1).Первичн
импликантой
бул ф-и назыв такая импликанта, никакая
часть которой не является импликантой
исходной функции. На данном этапе
рассматриваются все элементарн
конъюнкции (ЭК) ранга n, первоначально
входящие в СДНФ. Они попарно сравниваются
м\у собой с целью нахождения поглощ
вида:Fxi
v
Fxi
= F,при
кот получаются ЭК ранга (n – 1). После
получения всех возможных ЭК ранга (n –
1) они вновь сравниваются попарно между
собою для получения ЭК ранга (n – 2) и
т.д. ЭК, принявшие участие в поглощениях,
отмечаются некоторым символом. Процесс
заканчивается тогда, когда полученные
ЭК ранга m не склеиваются м\у собою. Все
не отмеченные ЭК будут являться
первичными импликантами.Для данного
построения целесообразно использовать
квадратные таблицы, размерностью l
x l,
где l
– число ЭК k-го ранга; k = n, n – 1, ...,
m.ЭТАП 2.
Расстановка меток и нахождение
существенных импликант.В результате
выполнения первого этапа минимиз ф-я
оказалась предст в виде:f
(x1,
x2,
..., xn)
=
![]() где
li
– первичные импликанты.Поэтому составл
таблица, строки кот соответ первичн
импликантам, а столбцы ЭК исх ф-и. Если
в некоторую ЭК входит одна из первичных
импликант, то на пересечении соответствующей
строки и столбца ставится метка. Если
после заполнения всей таблицы в некотором
столбце оказывается только одна метка,
то первичная импликанта, находящаяся
в данной строке, называется существенной.Из
таблицы исключаются строки, соответствующие
существенным импликантам, и столбцы
ЭК, покрываемых этими существенными
импликантами ЭТАП 3.
Вычеркивание избыточных столбцов и
избыточн первичных импликант.Если в
таблице полученной на предыдущем этапе
имеются столбцы, в которых метки
расположены в одинаковых строках, то
один из таких столбцов вычеркивается.
Так как покрытие оставшегося столбца
будет осуществлять покрытие удаленной
ЭК.Если после удаления избыточных
столбцов в таблице появляются строки,
в которых нет ни одной метки, то они
вычеркиваются, так как первичные
импликанты, соответствующие этим
строкам не покрывают оставшиеся в
рассмотрении ЭК.ЭТАП 4.
Выбор мин покрытия максимальными
интервалами.Из таблицы, полученной в
результате выполнения третьего этапа,
выбирается совокупность первичных
импликант, которая включает хотя бы по
одной метке в каждом столбце. При
нескольких возможных вариантах
выбирается покрытие минимальной
сложности.
где
li
– первичные импликанты.Поэтому составл
таблица, строки кот соответ первичн
импликантам, а столбцы ЭК исх ф-и. Если
в некоторую ЭК входит одна из первичных
импликант, то на пересечении соответствующей
строки и столбца ставится метка. Если
после заполнения всей таблицы в некотором
столбце оказывается только одна метка,
то первичная импликанта, находящаяся
в данной строке, называется существенной.Из
таблицы исключаются строки, соответствующие
существенным импликантам, и столбцы
ЭК, покрываемых этими существенными
импликантами ЭТАП 3.
Вычеркивание избыточных столбцов и
избыточн первичных импликант.Если в
таблице полученной на предыдущем этапе
имеются столбцы, в которых метки
расположены в одинаковых строках, то
один из таких столбцов вычеркивается.
Так как покрытие оставшегося столбца
будет осуществлять покрытие удаленной
ЭК.Если после удаления избыточных
столбцов в таблице появляются строки,
в которых нет ни одной метки, то они
вычеркиваются, так как первичные
импликанты, соответствующие этим
строкам не покрывают оставшиеся в
рассмотрении ЭК.ЭТАП 4.
Выбор мин покрытия максимальными
интервалами.Из таблицы, полученной в
результате выполнения третьего этапа,
выбирается совокупность первичных
импликант, которая включает хотя бы по
одной метке в каждом столбце. При
нескольких возможных вариантах
выбирается покрытие минимальной
сложности.
18) Аналитические способы минимизации (метод Квайна-МакКласки).Основным недостатком метода Квайна является необходимость полного по парного сравнения ЭК на этапе нахождения первичных импликант. Мак-Класки предложил модернизацию алгоритма Квайна, которая заключается в том, что все ЭК, входящие в СДНФ записывается в виде двоичных чисел (номеров наборов), которые группируются по числу входящих в них единиц в непересекающиеся классы. В класс с номером i войдут все ЭК содержащие в своей двоичной записи i единиц. По парное сравнение следует производить м\у соседними по номеру классами, т.к только в них могут находиться склеивающиеся ЭК.При образовании ЭК ранга меньше n вместо исключенных переменных ставится символ стирания x.когда дальнейшие склеивания не возможны, поэтому переходим ко второму этапу.
19) Понятие СДНФ, КДНФ, ТДНФ, МДНФ, СКНФ, МКНФ.Совершенная дизъюнктивная нормальная форма (СДНФ)Ф-я представляется суммой групп. Каждая группа состоит из произведения, в которую входят все переменные.Например: f(x1,x2,x3)=x1·x2·x3 + x1·x2·x3 + x1·x2·x3 Алгоритм построения СДНФ по таблице истинности1.В таблице истинности отмечаем те наборы переменных, на кот знач ф-и равно 1. 2.Для каждого отмеч набора записываем конъюнкцию всех перем по следующ правилу: е знач некоторой переменной есть 1, то в конъюнкцию включаем саму перем, иначе ее отрицание. 3.Все полученные конъюнкции связ операциями дизъюнкции.Совершенная конъюнктивная нормальная форма (СКНФ)Функция представляется произведением групп. Каждая группа состоит из суммы, в которую входят все переменные. Например: f(x1,x2,x3)=(x1+x2+x3) · (x1+x2+x3) · (x1+x2+x3) Минимальной ДНФ (МДНФ) ф-и f(x1, x2, …, xn) называется ДНФ, реализующая ф-ю f и содержащая мин число символов переменных по сравнен со всеми другими ДНФ, реализующими функцию f. МДНФ данной формулы м\найти, перебрав конечн число равносильных ей ДНФ и выбрав среди них ту, кот содержит мин число перем.при большом числе переменных такой перебор практически невыполним. Существуют эффект способы нахождения мДНФ. Рассмотрим два из них. Каждый из рассмотренных ниже методов состоит из двух этапов:-построение сокращенной ДНФ;-построение матрицы покрытий. Построение МДНФ. Тупиковой ДНФ (ТДНФ) функции f называется такая ДНФ ее простых импликант, из которых нельзя выбросить ни одного импликанта, не изменив функции f. Теорема. Всякая минимальная ДНФ некоторой функции является ее тупиковой ДНФ. Для получения МДНФ функции f необходимо построить все ТДНФ функции f и выбрать те из них, которые содержат минимальное число букв. КДНФ - каноническая дизъюнктивная нормальная форма
20) Алгоритм проектирования комбинационных схемПод комбинац схемой (КС) поним лог (цифр) сх, вх сигналы кот зависят только от значений вх сигналов в данный момент времени и не зависят от предшествующ вх и вых сигналов. Можно сказать, что КС - это правильная схема, постр из функц элементов, явл автоматами без памяти.правильной называют лог сх без обратных связей, соедин эл-тов в кот выполнены по правилам, соответ в функц отношении операции суперпозиции ф-й.Осн задачами теории КС явл задачи анализа и синтеза схем.Задача анализа состоит в нахожд общ конструктивн приема (алгоритма), позволяющ по любой КС построить ф-ю этой сх и по ней опр зав-ть сигнала на каждом из ее вых от сигналов на вх. Решение задачи состоит в выписывании суперпозиц ф-й, опред соединением эл схемы.Задача синтеза КС сводится к представ реализ ф-й в виде суперпозиции ф-й, реализ некоторым заранее заданным набором лог эл-ов.(Р)Данный алг м\видоизм-ся в конкр условиях проектирования.
21) Этапы синтеза КС:I Этап.1. По данному алг работы устр-ва выд независ перем (выходы датчиков, ключей, кнопок и т.п.).2. Выдел вых сигн схемы. Отмеч знач вых на кажд наборе аргум. Пров-ся независ состояния вых от последоват появл вх наборов. Е. зав-ть наблюд-ся, то это неКС и нужно пользоваться дрметодами.3. Состав табл истин или структур формула ф-и.II Этап.Провод-ся минимиз бул ф-и известн способами.III Этап.Мин дизъюнктивная норм форма предст-ся в виде суперпоз-и элементар наборов в зав-ти от элементн базиса, имеющегося от разработчика.
22)Приведение
булевых функций к данному функциональному
базису и построение функциональной
схемыД\получ
функц сх, соответствующ заданной ф-и
ал, необходимо выразить ф-ю в некот
функцион-полном базисе и сопост каждой
элементар ф-и функцион элемент ей
соответствующ. Процесс такого преобразов
сост в последовательн декомпоз исх
формы представлен зад ф-и на подф-и,
представле в зад функц базисе и
продолжается до тех пор, пока не будет
найдена эквивалент БФ в требуемом
базисе.Разработать КС для системы охр
сигнализ, кот выдает сигнал тревоги
если сраб 1из2датчиков на окнах или
датчик на вх двери или вместе и нет
сигнала снятия тревоги с пульта.I
Этап.Выделим одно исполн уст-во - электрич
сирену и 4 датч -2на окнах,1на двери и
датч снятия сигнала
тревоги с пульта охр. Введем обозначения:
Х1--сигнал
датч1окна, Х2-датч2окна,Х3-датч
дверей, Х4-снятия
тревоги с пульта. Сигн вкл электрич
сирены представ собой лог ф-ю вида:
у=f(X1,X2,X3,X4).
Построим Табл.истин д\функции у на
основе словесного алгоритма работы
схемы. Получим запись функции![]() II
Этап.Выполним минимиз лог, использ к
Карно. Получим:
II
Этап.Выполним минимиз лог, использ к
Карно. Получим:![]() III
и IV Этапы.Рассмотрим полученные функции
у в различ базисах.В баз 2И-НЕ
получим:
III
и IV Этапы.Рассмотрим полученные функции
у в различ базисах.В баз 2И-НЕ
получим:![]() Обозначим
Обозначим
![]() Постр
сх в базисе 2ИЛИ-НЕ.Обозначим
Постр
сх в базисе 2ИЛИ-НЕ.Обозначим
![]()
![]() Попробуем
использовать базис 2И–НЕ, 2ИЛИ
Попробуем
использовать базис 2И–НЕ, 2ИЛИ![]() М\построить
бесконеч число вариантов эквивал функц
схем.схемы будут эквивал логически, но
не схемотехнически (по кол-ву функц
эл-ов, корпусов, v
и s).
М\построить
бесконеч число вариантов эквивал функц
схем.схемы будут эквивал логически, но
не схемотехнически (по кол-ву функц
эл-ов, корпусов, v
и s).
24)
Синтез КС с несколькими выходамиКС
с несколькими выходами м\б описано
системой бул ф-й вида:т.е она должна на
одних и тех же наборах вх перем формир
несколько вых разрядов.Нетрудно понять,
что существует тривиальный метод
проектирования КС с нескольикми
выходами, который заключается в том,
что каждая функция из системы реализуется
отдельно КС. При этом структура такой
КС будет иметь вид:Такой метод реализации
является заведомо избыточным, т.к.
функции, входящие в систему могут
содержать одинаковые ЭК или скобочные
выражения. Известен метод совместной
минимиз системы БФ, который заключается
в нахождении совместных импликант и
построении МДНФ системы функции через
такие импликанты. Данный метод
предусматривает нахождение всех
конъюкций вида:Процесс построения
таких произведений достаточно трудоемок,
а результаты совместной минимизации
часто оказываются незначительными для
КС средней сложности (n = 3
![]() 6,
m = 3
6).При
n и m больших, чем 6-7 реализация метода
совместной импликации вручную становится
практически невозможной. Поэтому, с
точки зрения инженерной практики,
целесообразно выполнять минимизацию
функций системы (4.4.1.) по отдельности,
а затем найти или выделить совпадающие
ЭК или более сходные фрагменты. При
этом открываются широкие возможности
поиска оптимальных реализаций, как и
для КС с одним выходом
6,
m = 3
6).При
n и m больших, чем 6-7 реализация метода
совместной импликации вручную становится
практически невозможной. Поэтому, с
точки зрения инженерной практики,
целесообразно выполнять минимизацию
функций системы (4.4.1.) по отдельности,
а затем найти или выделить совпадающие
ЭК или более сходные фрагменты. При
этом открываются широкие возможности
поиска оптимальных реализаций, как и
для КС с одним выходом
25АвтоматноепреобразованиеинформацииРезультат
преобразования в\в зависит не только
от того какая информация появилась на
вх , но и от предысто преобразования.
Сущ более сложные не функц преобразов
инфо. Их реализ зависит не только от вх
но и от того что было на вх раньше. Такие
преобразов называют автоматами.Число
возможных вх историй бесконечно. На
мн-ве предыст вводится отнош эквивал-ти.
2 предыст считают эквивал,е.они одинаковым
образом, влияют на дальнейш поведение
автомата. Для своего функционир автомат
не обязательно должен запоминать все
вх истории. Достаточно запомнить класс
эквивал кот принадлежит та или иная
история. Ситуация, когда кол-во классов
эквивал вх истории конечно, явл
простейшей. Соответств вх модель назыв
конечн автоматным преобразоват инфо
или КА.Внутр сост автом назыв класс
эквивален его вх историй. Неформально
состояние системы - это хар-ка, однозначно
определяющ ее дальнейш поведение, а
также все последующ реакции системы
на внеш события.На1 и тот же вх сигнал
КА может реагир по-разному, в зав-ти от
того в каком состоянии он находится в
данный момент.Сост представл собой
класс эквивал предысторий вх, сост
м\изменятся только при прих очередн вх
сигнала. При получ вх сигнала КА выдает
не только инфо на вх как ф-ю этого вх
сигн и сост, но и меняет свое состояние.
Функц автомата удобно представлять
графВ
БП
автомата хранит инф. о текущ сост S,
кот вместе с вх сигн х опред вых реакцию
авт-а y
и след состояние S'.
На вход КА в каждом такте поступает
один из возможных вх сигн, а на его вых
появляется вых сигнал, явл ф-й его текущ
сост и поступивш вх сигн внутрен сост
также меняется. Моменты сраб определ
либо принудительно (тактирующим
синхросигналом), либо асинхронно
(наступление внешнего события).КА: S-конечное
непустое множество множества
состояний.Х--конечное непустое множество
входных сигналов (входной алфавит)У--конечное
непустое множество выходных сигналов
(выходной алфавит)s0-
начальное состояние;
S-конечное
непустое множество множества
состояний.Х--конечное непустое множество
входных сигналов (входной алфавит)У--конечное
непустое множество выходных сигналов
(выходной алфавит)s0-
начальное состояние;
 -функция
перехода.
-функция
перехода.
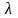 -функция
выходов.Представление КА: графическое,
табличное
-функция
выходов.Представление КА: графическое,
табличное
26 Реализация конечных автоматов:2реализации: программная,аппаратнаяПрограммная(составление блок схем программ работы автомата и самой программы)Пример: Автомат .Топология блок схемы прогр повторяет топологию графа. С каждым состоянием связана операция NEXT, выполняющ функц ожид очередн сигн и чтение его в некоторый станд буфер и послед анализ, какой это сигнал. В зав-ти от того, какой сигнал пришел на вход, выполняется та или иная ф-я(Y0..Y5), и происходит переход к след состоянию. АппаратнаяТребует построения ус-в памяти для запом текущ состояния автомата (триггеры).Функциональный блок автомата реализуется как конечный преобразователь.Общий подход к реализации:1) кодирование вход и вых сигналов двоичном виде2)по таблицам переходов и вых составляются кодир таблицы переходов и вых.3) по код табл проводится минимиз двоичн ф-й в зад базисе4) решаются вопросы синхронизации, т.е. привязки моментов выдачи выходного сигнала и изменения состояния внутр памяти моментным поступлением вх сигналов.
28
Минимизация конечных автоматов.Разные
автоматы могут функц одинаково даже,
е. у них разное число состояний. Важной
задачей явл нахождение мин автомата,
кот реализ заданное автоматн отображ.
Эквивалент естеств считать 2 автомата
которые нельзя различить никакими вх
сигналами. 2 состояния P
и Q
некоторого автомата А называются эквив
если справедливо след утверждение. Люб
цепочка поданная на автомат в состоянии
q0
даст такую же реакцию как, когда автомат
находится в состоянии q2.Эквивал
состояния м\объединять в 1класс,
состоянием кот явл классы эквивалент
состояний.Е.мы можем опред на мн-ве сост
автомата макс возможные разбиения на
классы, то выбирая классы эквивал как
новое состояние получим мин автомат
эквивалент исходному.Сущ алгоритм
опред мин отношения эквивалент на мн-ве
состояний КА.Алгоритм состоит в
последовательном построении на мн-ве
состояний автомата А классов разбиений,
таких что в1класс разбиения
Люб
цепочка поданная на автомат в состоянии
q0
даст такую же реакцию как, когда автомат
находится в состоянии q2.Эквивал
состояния м\объединять в 1класс,
состоянием кот явл классы эквивалент
состояний.Е.мы можем опред на мн-ве сост
автомата макс возможные разбиения на
классы, то выбирая классы эквивал как
новое состояние получим мин автомат
эквивалент исходному.Сущ алгоритм
опред мин отношения эквивалент на мн-ве
состояний КА.Алгоритм состоит в
последовательном построении на мн-ве
состояний автомата А классов разбиений,
таких что в1класс разбиения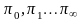 попадают k
состояния, которые неразличимы вх
цепочками длинной k.
Такие
состояния счит находящ в отнош эквивалент
k.
Если
выполняется условие
попадают k
состояния, которые неразличимы вх
цепочками длинной k.
Такие
состояния счит находящ в отнош эквивалент
k.
Если
выполняется условие
 ,
то тогда p и q называются к-различимыми.
,
то тогда p и q называются к-различимыми. Очевидно,
что все состояния в автомате ноль
эквивалентны, при подаче пустых цепочек
на вх автомата, вых также явл пустая
цепочка независ от состояния , в кот
находится автомат.Разбиение пи1 легко
построить. В один блок пи1 попадают все
состояния, в которых автомат одинаково
реагирует на входные сигналы.
Очевидно,
что все состояния в автомате ноль
эквивалентны, при подаче пустых цепочек
на вх автомата, вых также явл пустая
цепочка независ от состояния , в кот
находится автомат.Разбиение пи1 легко
построить. В один блок пи1 попадают все
состояния, в которых автомат одинаково
реагирует на входные сигналы.
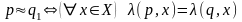 Разбиение
пи0 содержащее один единственный блок,
в который входят все состояния автомата
и разбиения пи1, в каждом блоке которого
собрано состояние неразличимое входными
сигналами, является исходным при
построении цепочки разбиения
Определив
как строится след распред из предыдущ,
м\построить всю цепочку. Теорема: Если
Разбиение
пи0 содержащее один единственный блок,
в который входят все состояния автомата
и разбиения пи1, в каждом блоке которого
собрано состояние неразличимое входными
сигналами, является исходным при
построении цепочки разбиения
Определив
как строится след распред из предыдущ,
м\построить всю цепочку. Теорема: Если
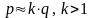 ,
то для того чтобы
,
то для того чтобы
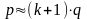 необходимо и достаточно чтобы выполнялось
следующ условие
необходимо и достаточно чтобы выполнялось
следующ условие Для
того что бы 2 к-эквивалент КА были бы
л+1-эквивалентн необходимо и достаточно,
чтобы под возд любого вх сигнала автомат
переходил в пару состояний, который
были бы к- эквивал.Д \т, чтобы вх цепочка
длинны к+1 не различала пару состояний
p и q нужно, чтобы автомат из этих
состояний переходил под воздействие
x0
в такие состояния, которые не различимы
цепочкой (x1
, x2
,… xk),
т.е.
Для
того что бы 2 к-эквивалент КА были бы
л+1-эквивалентн необходимо и достаточно,
чтобы под возд любого вх сигнала автомат
переходил в пару состояний, который
были бы к- эквивал.Д \т, чтобы вх цепочка
длинны к+1 не различала пару состояний
p и q нужно, чтобы автомат из этих
состояний переходил под воздействие
x0
в такие состояния, которые не различимы
цепочкой (x1
, x2
,… xk),
т.е.
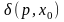 и
и
 были бы к-неразличимым.
были бы к-неразличимым.
31.
Моделирование систем и событий с помощью
сетей Петри.Реал
система функц во времени, событии
происходит в нек момент времени и
действует нек время. В синхр моделях
дискретн систем события явно привязаны
к некоторым моментам или интервалам
времени, в кот происх одноврем измен
состояния все компонентов системы,
т.е. измен состояния всей системы в
целом. Смена состояния системы происходит
последовательно. В с Петри обычно
отказываются от введения дискр времени
и тактированных последоват изменения
состояний, заменяя их причинно-следств
связями м\у событиями. Если же возникает
необход осуществит привязку ко времени,
то моменты или интервалы времени
представляют как события. Т.о. синхронные
системы могут описываться в терминах
асинхронных моделей. Отказ от времени
приводит к тому, что события в асинхр
модели просматрив как элементар или
составные. Взаимодействие событий в
сложных асинхр системах имеет как
правило сложн динам структуру. Глоб
ситуации в системе формир с пом-ю лок
операций, кот наз-ся условиями реализации
событий. Д\реш указанных задач дискр
системы достаточ представить, как
структуры, образованные из элементов2типов:
события и условия. В с.Петри они
представлены абстракт символами из 2
непересекающ алфавитов или мн-в, кот
назыв-ся соответств мн-вами позиций и
переходов. Условия и события переходы
связаны отнош непосредств зав-ти, кот
изображ с пом-ю направленных дуг.
Е.возникает необх-сть осущ привязку ко
времени, то моменты или интервалы
времени представ как события
С=(Р,Т,Е,W,М)
Р-множество позиций; Т-множество
переходов; Е-отношение инцидентности;
М-начальная маркировка сети; W-функция,
задающая кратность дуг.
![]() Выполнен
условий изображается разметкой, т.е.
помещением некоторого числа фишек в
позиции и места. Неформально работу
сетей можно представить как совокупность
локальных действий, которые называются
срабатыванием переходов. Они соответствуют
реализациям событий и приводят к
изменению разметки позиций, т.е. к
локальному изменению условий в системе.
С=(Р,Т,I,О)тождественно(Р,Т,Е).Маркировка
заключ в присвоении фишек или маркеров
позициям с.Петри. При работе сети фишки
в кружках перемещаются в выходные
позиции. Переход может сработать только
тогда, когда он разрешен.Е.в системе
нет одного перехода готового к
срабатыванию – это тупиковая ситуация.
Динамика сети Петри отражается в
изменении маркеровки. Пример:
Выполнен
условий изображается разметкой, т.е.
помещением некоторого числа фишек в
позиции и места. Неформально работу
сетей можно представить как совокупность
локальных действий, которые называются
срабатыванием переходов. Они соответствуют
реализациям событий и приводят к
изменению разметки позиций, т.е. к
локальному изменению условий в системе.
С=(Р,Т,I,О)тождественно(Р,Т,Е).Маркировка
заключ в присвоении фишек или маркеров
позициям с.Петри. При работе сети фишки
в кружках перемещаются в выходные
позиции. Переход может сработать только
тогда, когда он разрешен.Е.в системе
нет одного перехода готового к
срабатыванию – это тупиковая ситуация.
Динамика сети Петри отражается в
изменении маркеровки. Пример:
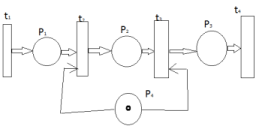 Требуется
описать с помощью сПетри работу группы
пользователей на единств рабочей
станции при зад хар-ках потока запроса
на её использование и хар-ках поступ
задач.
Требуется
описать с помощью сПетри работу группы
пользователей на единств рабочей
станции при зад хар-ках потока запроса
на её использование и хар-ках поступ
задач. -
поступл запроса на использ станции;
-
поступл запроса на использ станции;
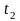 -
занятие станции;
-
занятие станции;
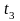 -освобожд
станции;
-освобожд
станции;
 -
выход обслуж заявки.
-
выход обслуж заявки.
 используется д\отображения состояния
станции, если в
есть метка, это означает, что станция
свободна и пришедш заявка вызывает
срабатывание
,
пока заявка не будет обработана.
используется д\отображения состояния
станции, если в
есть метка, это означает, что станция
свободна и пришедш заявка вызывает
срабатывание
,
пока заявка не будет обработана.
32.
Расширения сетей Петри.Ингибиторные
сети
– это сПетри, дополн спец ингибиторными
дугами. Переход в ингибит сети может
сработать , если каждая его вх поз ,
соедин с переходом обычной дугой
кратностью W(P,t)
,содержит не менее W(P,t)
фишек . А кажд вх поз, соедин с переходом
ингибит дугой , имеет нул разметку .
Весь вес ингибит дуги всегда равен
1.Приоритетные
сПетри.Здесь
вводятся приоритеты срабатывания
переходов.Если в сети существует
несколько переходов готовых к
срабатыванию. Структурированные
сПетри.Здесь
некоторые из переходов явл. сложными.
При их срабатывании запускается сеть,
др условия иерархии исп-ся для моделир
модульн вычислит систем.Цветные
сП.Введение
набора цветов фишек исп-ся для моделир
аппаратн средств фишек использ
д\моделирования аппарат средств.Сети
с измен структурой, кратность ребер не
явл постоянной. Существуют временные
с П.,
в них переходам ставится в соответствующее
время нахождения фишки внутри этой
позиции.Стахостические
сети.Элементарные сети П.-
может одновременно присутствовать
только1фишка, вес дуг всегда еденица.Сущ-ют
сети П. высокого
уровня –
наличие возможности применять
цвета.Дискретные
непрерывные сети П.:ДНСП= Уравнение
динамики для непрерывных сПетри:
Уравнение
динамики для непрерывных сПетри: ,
, -
функция;
-
функция;
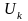 -
управляющий вектор;
-
управляющий вектор;
 -
транспонированная матрица.Элементы
управл.вектора принимают значения 0
или 1, 1 - если даны переход готов к
срабатыванию , 0- если нет.
отражает
структуру сети, показывает какое
количество фишек перем-ся между позицией
и переходом.Вложенные
сети П.
состоят из сист сети и элемент сетей,
представляющ собой обыкнов сети П. Во
вложенных сетях существуют элементарн
и сетевые фишки.Динамика поведения в
ложной сети харак-ся 4-мя шагами:1.
срабатыв переходов сист сети в соот-ии
с паравилами; 2. срабатывание преходов
в элемент сетях; 3. шаг гор синхронизации,
срабатывание переходов, помеченных
особым символом; 4. шаг вертик
синхронизации.Гибридные
сети отличаются математическим
описанием.
-
транспонированная матрица.Элементы
управл.вектора принимают значения 0
или 1, 1 - если даны переход готов к
срабатыванию , 0- если нет.
отражает
структуру сети, показывает какое
количество фишек перем-ся между позицией
и переходом.Вложенные
сети П.
состоят из сист сети и элемент сетей,
представляющ собой обыкнов сети П. Во
вложенных сетях существуют элементарн
и сетевые фишки.Динамика поведения в
ложной сети харак-ся 4-мя шагами:1.
срабатыв переходов сист сети в соот-ии
с паравилами; 2. срабатывание преходов
в элемент сетях; 3. шаг гор синхронизации,
срабатывание переходов, помеченных
особым символом; 4. шаг вертик
синхронизации.Гибридные
сети отличаются математическим
описанием.
33.
Понятие структурного синтеза автоматов.
Теорема о структурной полноте.Процесс
постр сх автомата обычно разделяют на
две стадии: 1.абстрактный синтез; 2.
структурный синтез.На стадии абстр.
Синтеза вып-ся построение табл переходов
и выходов автомата. На стадии структ.
синтеза вып-ся схемная реализация
абстрактного автомата, т.е. строится
структ. автомат из более простых
автоматов, называемых элементарными.
Элементарные автоматы бывают двух
видов: авт-т с памятью, имеющие более
одного состояния и авт-ты без памяти –
с одним состоянием. Авт-ты с памятью
наз-ют элементами памяти или запоминающие
элементы, авт-ты без памяти – комбинационные
или лог элементы. Элементы памяти
соединяются между собой с помощью лог
элементов (и, или, не). При структурном
синтезе авт-та необходимо выбрать
систему элементов, из которых в дальнейшем
будет строиться авт-т. Д.т.ч м\б построить
сх любого КА, такая система авт-ов должна
быть структурно полной. Теорема:
система
элемент авт-ов, содержащ функцион полную
систему логич эл-ов, хотя бы один авт-т
Мура с памятью, обладающ полной сист
перех и полн сист вых, явл структурно
полной. Полнота перех в автоматах
означает след-ее: для люб пары состояний
 сущ
хотя бы один вх сигнал, к-ый переводит
авт-т из состояния
сущ
хотя бы один вх сигнал, к-ый переводит
авт-т из состояния
 в сост-ие
в сост-ие
 .
В авт-те, обладающ полной сист перех
д\встречаться все состояния. Полнота
выхода авт-та отлич следующ: в кажд сост
автомат выдает вых сигнал, отличн от
сигналов, выдаваемых в др. состояниях.
Требование полноты сист вых связано с
необходим различ внутр сост элементар
авт-ов. Т.к. в авт-те, необладающ полн
сист вых различ сост невозм=>невозмож
обеспеч зад усл функционир системы.
Авт-т Мура удовлетворяет требованиям
и полноте системы и выходов. Цель
структурного синтеза авт-та заключается
в построении цифр схемы авт-та на основе
системы лог уравн, в кот записыв завис
вых сигналов авт-тв и сигн, подав на вх
запом эле-ов от вх сигналов авт-та и
сигн с вых элем-ов памяти.
.
В авт-те, обладающ полной сист перех
д\встречаться все состояния. Полнота
выхода авт-та отлич следующ: в кажд сост
автомат выдает вых сигнал, отличн от
сигналов, выдаваемых в др. состояниях.
Требование полноты сист вых связано с
необходим различ внутр сост элементар
авт-ов. Т.к. в авт-те, необладающ полн
сист вых различ сост невозм=>невозмож
обеспеч зад усл функционир системы.
Авт-т Мура удовлетворяет требованиям
и полноте системы и выходов. Цель
структурного синтеза авт-та заключается
в построении цифр схемы авт-та на основе
системы лог уравн, в кот записыв завис
вых сигналов авт-тв и сигн, подав на вх
запом эле-ов от вх сигналов авт-та и
сигн с вых элем-ов памяти.
34. Типы элементарных автоматов памяти. Триггеры.В настоящ время в выч технике используются элементар автоматы, имеющие след особенности:1. Элементарн авт-ты явл автом Мура с2внутрен состоян;2. Авт-т выдает 2различных вых сиг, соответс 2его внутр состояниям;3. Элемент авт-ты м\иметь в общем случае несколько физич вх, на каждый из которых могут подавать сигналы, закодированные цифры 0 и 1.
![]() В
кач-ве эл-ых авт-ов в выч технике обычно
исп-ся триггеры различных типов. Триггер-
это устр-во, имеющ 2сост, в кот он переходит
под действием вх сигналов. Выделяют
информац и синхросигн. Информац сигналы
определяют новое состояние триггера
и присутствуют в люб триггерах. По типу
инф. сигналов сущ-ют след класс-ция
триггеров:D,T,RS,JK
– триггеры. RST,DV
– триггеры и т.д.Синхросигн С не явл
обяз и вводится в триггерах с целью
фиксац мом перехода триг в новое сост,
на него поступают импульсы генератора,
синхронизир работу цифр авт-та. Период
следования импульсов соответст1такту
автоматн времени.Т-триггер назыв авт-т
Мура с2уст-ми состояниями и 1входом,
к-ые изменяют свое сост на противополож,
когда на вх поступает новый вх сигнал.
Т- триггер наз-ют триггером со счетным
входом. В соответствии с состоянием,
принимаемым триггером, вход S-
единичный, R-
нулевой, поэтому переход в триггере не
определен.Таблица переходов:
В
кач-ве эл-ых авт-ов в выч технике обычно
исп-ся триггеры различных типов. Триггер-
это устр-во, имеющ 2сост, в кот он переходит
под действием вх сигналов. Выделяют
информац и синхросигн. Информац сигналы
определяют новое состояние триггера
и присутствуют в люб триггерах. По типу
инф. сигналов сущ-ют след класс-ция
триггеров:D,T,RS,JK
– триггеры. RST,DV
– триггеры и т.д.Синхросигн С не явл
обяз и вводится в триггерах с целью
фиксац мом перехода триг в новое сост,
на него поступают импульсы генератора,
синхронизир работу цифр авт-та. Период
следования импульсов соответст1такту
автоматн времени.Т-триггер назыв авт-т
Мура с2уст-ми состояниями и 1входом,
к-ые изменяют свое сост на противополож,
когда на вх поступает новый вх сигнал.
Т- триггер наз-ют триггером со счетным
входом. В соответствии с состоянием,
принимаемым триггером, вход S-
единичный, R-
нулевой, поэтому переход в триггере не
определен.Таблица переходов:
-
R
S

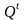
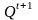
0
0
0
0
0
0
1
1
0
1
0
1
0
1
1
1
1
0
0
0
1
0
1
0
1
1
0
-
1
1
1
-
Таблица функций:
-

S
0
0
х
0
0
1
0
1
1
0
1
0
1
1
0
х
J |
K |
Q(t) |
Q(t+1) |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
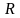 является безразличным, поэтому стоит
в таблице переменная х, к-ая может
принимать два значения 0 или 1. Аналогично
1 в 1 при R=0
S=0,
R=0
S=1,
поскольку при таком переходе S-
безразлично, то переменная х. Авт-ты,
к-ые могут переходить из одного состояния
в другое под действтем нескольких
комбинаций входных сигналов, наз-ся
авт-ми с избыточной системой переходов.
Избыточность можно использовать для
упрощения схемы, придавая переменной
х такие значения, которые позволяют
минимизировать число элементов, поэтому
если схемы двух элементарных автоматов
равноценны по сложности, то предпочтение
авт-ту, имеющему большую систему
переходов.Закон функционирования
является безразличным, поэтому стоит
в таблице переменная х, к-ая может
принимать два значения 0 или 1. Аналогично
1 в 1 при R=0
S=0,
R=0
S=1,
поскольку при таком переходе S-
безразлично, то переменная х. Авт-ты,
к-ые могут переходить из одного состояния
в другое под действтем нескольких
комбинаций входных сигналов, наз-ся
авт-ми с избыточной системой переходов.
Избыточность можно использовать для
упрощения схемы, придавая переменной
х такие значения, которые позволяют
минимизировать число элементов, поэтому
если схемы двух элементарных автоматов
равноценны по сложности, то предпочтение
авт-ту, имеющему большую систему
переходов.Закон функционирования
 -
триггеров:
-
триггеров:
 при
при

 -
триггеры- универсальный авт-т Мура с
двумя усталостными состояниями и двумя
входами J
и K,
в котором приусловии JxK=1
осуществляет инверсию предыдущего
состояния, а в остальных случаях
функционирует в соответствии с таблицей
истинности
-
триггеры- универсальный авт-т Мура с
двумя усталостными состояниями и двумя
входами J
и K,
в котором приусловии JxK=1
осуществляет инверсию предыдущего
состояния, а в остальных случаях
функционирует в соответствии с таблицей
истинности
 -
триггеров, при этом вход
-
триггеров, при этом вход
 эквивалентен
входу S,
а вход К входу R.
Этот триггер не имеет запрещенной
комбинации входных сигналов, а таблица
истинности имеет след-ий вид:
Q(t+1)=f(J,K,Q(t)
эквивалентен
входу S,
а вход К входу R.
Этот триггер не имеет запрещенной
комбинации входных сигналов, а таблица
истинности имеет след-ий вид:
Q(t+1)=f(J,K,Q(t)
Триггер относится к разряду универсальных, т.к. на его основе можно построить RS,D,T- тригерры. RS тр. получается из JK – триггера наложением ограничений на комбинацию входных сигналов J=K=1, т.к. эта комбинация является запрещенной для RS – триггеров.
![]() Счетный
триггер получается путем объединения
входов
и
К.
Счетный
триггер получается путем объединения
входов
и
К.
 -
триггер строится путем подключения к
входу инвектора, на который подается
тот же сигнал что и на вход J.
В этом случае вход J
выполняет функцию входа D,
а все устройство в целом реализует
таблицу переходов D-
триггера. В интегральной технике
применяется только синхронные JK-
триггеры, которые при С=0 сохраняют свое
состояние, а при С=1 работают как
асинхронные триггеры.
-
триггер строится путем подключения к
входу инвектора, на который подается
тот же сигнал что и на вход J.
В этом случае вход J
выполняет функцию входа D,
а все устройство в целом реализует
таблицу переходов D-
триггера. В интегральной технике
применяется только синхронные JK-
триггеры, которые при С=0 сохраняют свое
состояние, а при С=1 работают как
асинхронные триггеры.
35.
Канонический метод структурного синтеза
авт-та.На
стадии абстрактного синтеза обычно
используется представление авт-та в
виде1блока, имеющ 1вх и 1вых. На стадии
структур синтеза авт-та авт-т изображают
в виде обобщенной структурн схемы, в
которой есть l-входных
и l-выходных
сигналов, по которым предаются движения
сигналов
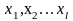 (входные
переменные) и
(входные
переменные) и
 (
выходные переменные или функции выхода
авт-та.
(
выходные переменные или функции выхода
авт-та.
П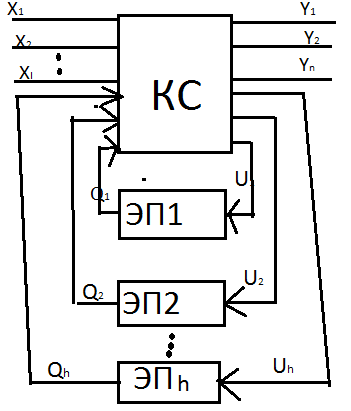 редставляется
обобщенная схема авт-та, состоящая из
двух частей: комбинационной схемы и
набора элементов памяти. Переменные
редставляется
обобщенная схема авт-та, состоящая из
двух частей: комбинационной схемы и
набора элементов памяти. Переменные
 соответствуют выходным сигналам
элементов памяти, называют внутренними
переменными авт-та.
соответствуют выходным сигналам
элементов памяти, называют внутренними
переменными авт-та.
 используются в схеме для обозначения
сигналов, изменяющих состояние элементов
в памяти. Их называют функциями
возбуждения. В качестве элементов
памяти на практике чаще всего используют
элементарные авт-ты, которые имеют
только входные и выходные линии. Каждое
состояние абстрактного авт-та
кодируются в структурных авт-ах набором
состояний элементов памяти. Если все
авт-ты одинаковые, то их число определяется
следующим выражением R≥
используются в схеме для обозначения
сигналов, изменяющих состояние элементов
в памяти. Их называют функциями
возбуждения. В качестве элементов
памяти на практике чаще всего используют
элементарные авт-ты, которые имеют
только входные и выходные линии. Каждое
состояние абстрактного авт-та
кодируются в структурных авт-ах набором
состояний элементов памяти. Если все
авт-ты одинаковые, то их число определяется
следующим выражением R≥ .
M-
число состояний синтезируемого авт-та.
b-
число состояний элементарного авт-та.
Обычно для элементарного авт-та b=2=>
R≥
.
M-
число состояний синтезируемого авт-та.
b-
число состояний элементарного авт-та.
Обычно для элементарного авт-та b=2=>
R≥ .
В отличие от абстрактного авт-та,
имеющего один входной и один выходной
канал, структурный авт-т имеет l-входных
и n-
выходных каналов. Каждый входной и
выходной сигнал абстрактного авт-та
могут быть закодированы двоичным
набором состояний входных и выходных
каналов структурного авт-та. Число
каналов l
и n
можно определить по следующим формулам:
l
≥]
.
В отличие от абстрактного авт-та,
имеющего один входной и один выходной
канал, структурный авт-т имеет l-входных
и n-
выходных каналов. Каждый входной и
выходной сигнал абстрактного авт-та
могут быть закодированы двоичным
набором состояний входных и выходных
каналов структурного авт-та. Число
каналов l
и n
можно определить по следующим формулам:
l
≥] [; n
≥]
[; n
≥] [ , где m
и k-
количество символов во входной и
выходном алфавитах абстрактного авт-та.
Для того чтобы структурный авт-т перешел
из одного состояния в другое необходимо
изменить состояние элементов памяти.
Изменение состояния элементов памяти
происходит под действием сигналов
,
поступающих на их вход. На вход сКС,
кроме вх сигнала, по цепи обратной связи
поступают сигналы
,
называемые функцией обратной связи от
памяти авт-та КС. Структурный синтез
конечных авт-ов заключается в выборе
типов элементарных авт-ов, в состоянии
функций возбуждения каждого элементарного
авт-та и функции кодированных выходов
авт-а.
[ , где m
и k-
количество символов во входной и
выходном алфавитах абстрактного авт-та.
Для того чтобы структурный авт-т перешел
из одного состояния в другое необходимо
изменить состояние элементов памяти.
Изменение состояния элементов памяти
происходит под действием сигналов
,
поступающих на их вход. На вход сКС,
кроме вх сигнала, по цепи обратной связи
поступают сигналы
,
называемые функцией обратной связи от
памяти авт-та КС. Структурный синтез
конечных авт-ов заключается в выборе
типов элементарных авт-ов, в состоянии
функций возбуждения каждого элементарного
авт-та и функции кодированных выходов
авт-а.
36.
Понятия синхронного и асинхронного
автоматов.Различие
м\у синхронными и асинхронными авт-ми
обусловлено задержками распространения
сигнала в элементах, с которых построен
авт-т, а также физическими принципами
работы устройств схемы авт-та. Синхронный
авт-т может изменять своё состояние
только в определенные моменты времени,
а именно в моменты поступления
синхронизированных импульсов. В отличие
от синхр-ых, асинхронный авт-т переключается
в момент изменения логического значения
входных сигналов. Входные сигналы
асинхронного автомата обладают
следующими свойствами: 1. сигнал
присутствует на входе авт-та в каждый
момент времени; 2. Длительность входного
сигнала неограниченна и превышает
некоторую минимальную величину; 3.
изменения входного сигнала могут
происходить в произвольные моменты
времени. При функционировании авт-та
могут появляться состязания. Это явление
возникает вследствие того, что элементы
памяти имеют различные достаточно
близкие времена срабатывания. Также
различны задержки сигналов возбуждения,
поступающих на входные каналы эл-ых
авт-ов по логическим цепям неодинаковой
длины. Если при переходе авт-та из одного
состояния в другое должны изменять
свое состояние сразу несколько
запоминающих элементов, то между ними
начинаются состязания. Тот элемент,
который выиграет эти состязания, т.е.
изменит свое состояние ранее чем другой,
может через цепь обратной связи изменить
сигналы на входах некоторых запоминающих
элементов до того, как другие участники
состязаний изменят свои состояния. Это
может привести к переходу авт-та в
состояние, непредусмотренное его
графом, поэтому в процессе перехода из
состояния
 в состояние
в состояние
 под действием некоторого входного
сигнала
под действием некоторого входного
сигнала
 авт-т
может оказаться в состоянии
авт-т
может оказаться в состоянии
 или
или
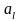 .Если
и далее при том же входном сигнале
авт-т
из состояния
и
перейдет в состояние
,
то такие состояния называются допустимыми
или некритическими. Если в этом автомате
есть переход из состояния
в некоторое состояние
,
отличное от
,
под действием того же сигнала
,
то авт-т может перейти в состояние с
индексом j.
Правильность его работы будет нарушена.
Такие состязания называются критическими
или гонками. Следует принимать меры
для их устранения.
.Если
и далее при том же входном сигнале
авт-т
из состояния
и
перейдет в состояние
,
то такие состояния называются допустимыми
или некритическими. Если в этом автомате
есть переход из состояния
в некоторое состояние
,
отличное от
,
под действием того же сигнала
,
то авт-т может перейти в состояние с
индексом j.
Правильность его работы будет нарушена.
Такие состязания называются критическими
или гонками. Следует принимать меры
для их устранения.![]()
37.
Гонки в автоматах. Устранение гонок.При
функционировании авт-та могут появляться
состязания. Это явление возникает
вследствие того, что элементы памяти
имеют различные достаточно близкие
времена срабатывания. Также различны
задержки сигналов возбуждения,
поступающих на входные каналы эл-ых
авт-ов по логическим цепям неодинаковой
длины. Если при переходе авт-та из одного
состояния в другое должны изменять
свое состояние сразу несколько
запоминающих элементов, то между ними
начинаются состязания. Тот элемент,
который выиграет эти состязания, т.е.
изменит свое состояние ранее чем другой,
может через цепь обратной связи изменить
сигналы на входах некоторых запоминающих
элементов до того, как другие участники
состязаний изменят свои состояния. Это
может привести к переходу авт-та в
состояние, непредусмотренное его
графом, поэтому в процессе перехода из
состояния
в состояние
под действием некоторого входного
сигнала
авт-т
может оказаться в состоянии
или
.Если
и далее при том же входном сигнале
авт-т
из состояния
и
перейдет в состояние
,
то такие состояния называются допустимыми
или некритическими. Если в этом автомате
есть переход из состояния
в некоторое состояние
,
отличное от
,
под действием того же сигнала
,
то авт-т может перейти в состояние с
индексом j.
Правильность его работы будет нарушена.
Такие состязания называются критическими
или гонками. Следует принимать меры
для их устранения.
Устранить
гонки можно аппаратными средствами,
либо использовать специальные методы
кодирования.Один из способов ликвидации
гонок это тактирование вх. Сигналов
автомата импульсами определенной
длительности .Предполагается что кроме
вх.сигналов существует еще канал С
от генератора синхро-импульсов , по
которому поступает сигнал С=1в момент
прихода импульса и С=0 при его отсутствии
.В связи с этим вх. Сигналом на переходе
существует еще канал С
от генератора синхро-импульсов , по
которому поступает сигнал С=1в момент
прихода импульса и С=0 при его отсутствии
.В связи с этим вх. Сигналом на переходе
 будет не сигнал Zf
, а сигнал
будет не сигнал Zf
, а сигнал
 .
Если длителбность импульса
.
Если длителбность импульса
 меньше
самого короткого пути прохождения
тактируемого сигнала обратной связи
по КС , то к моменту перехода в промежуточное
состояние
меньше
самого короткого пути прохождения
тактируемого сигнала обратной связи
по КС , то к моменту перехода в промежуточное
состояние
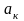 сигнал С=0 ,
=0,
что исключает гонки . Канал С практически
является синхро входом триггера .
Недостаток метода – трудность подбора
требуемой длительности импульса, т.к
она зависит от многих факторов , не
поддающихся строгому учету . Другой
способ ликвидации гонок заключается
в введении двойной памяти . в этом случае
каждый эл. Памяти дублируется , причем
перепись из первого эл. Памяти во второй
происходит , когда С=0 . сигналы обратной
связи для получения фун-ии возбуждения
и ф-ии выхода автомата снимаются с
выхода второго триггера . Т.О состязания
могут возникнуть только между первыми
триггерами . выходы вторых триггеров
не могут изменятся до тех пор, пока С
не станет равным 0. В этом случае сигнал
равно 0 , тогда первый триггер первым
перестанет воспринимать информацию и
гонок не будет . Для устранения гонок
используются спец. Методы противогоночного
кодирования . Среди которых чаще всего
применяется соседнее кодирование
состояния автомата , при котором условие
отсутствия гонок всегда выполнены при
соседнем кодировании любые два состояния,
связанные дугой на графе автомата,
кодируются наборами ,отличающимися
состояниями лишь одного эл. Памяти .
Соседнее кодирование возможно не всегда
. Граф автомата , допускающего соседнее
кодирование должен удовлетворять ряду
требований : 1- в графе автомате не должно
быть циклов с не четным числом вершин
2- два соседних состояния второго порядка
не должны иметь более двух состояний
, лежащих между ними. Под состояниями
второго порядка понимаются такие два
состояния , путь между которыми по графу
автомата состоит из двух ребер не
зависимо от ориентации . при соседнем
кодировании обычно пользуются картой
Карно . В этом случае состояние , связанное
дугой , располагают на соседних клетках
карты. При соседнем кодировании на
каждом переходе переключается только
один триггер, что принципиально устраняет
гонки. Анализ метода структурного
синтеза автомата показывает ,что
различные варианты кодирования состояния
автомата приводят к различным выражениям
функции возбуждения памяти и ф-ии выхода
, в результате чего сложность комбинационной
схемы существенно зависит от выбранного
кодирования . Среди множества алгоритмов
кодирования имеются два наиболле часто
встречающихся 1- алгоритм кодирования
для D-
триггеров ,2- эвристический алгоритм
кодирования. Алгоритм кодирования для
D-
триггеров : при кодировании не обходимо
выполнить следующее 1- каждому состоянию
автомата
сигнал С=0 ,
=0,
что исключает гонки . Канал С практически
является синхро входом триггера .
Недостаток метода – трудность подбора
требуемой длительности импульса, т.к
она зависит от многих факторов , не
поддающихся строгому учету . Другой
способ ликвидации гонок заключается
в введении двойной памяти . в этом случае
каждый эл. Памяти дублируется , причем
перепись из первого эл. Памяти во второй
происходит , когда С=0 . сигналы обратной
связи для получения фун-ии возбуждения
и ф-ии выхода автомата снимаются с
выхода второго триггера . Т.О состязания
могут возникнуть только между первыми
триггерами . выходы вторых триггеров
не могут изменятся до тех пор, пока С
не станет равным 0. В этом случае сигнал
равно 0 , тогда первый триггер первым
перестанет воспринимать информацию и
гонок не будет . Для устранения гонок
используются спец. Методы противогоночного
кодирования . Среди которых чаще всего
применяется соседнее кодирование
состояния автомата , при котором условие
отсутствия гонок всегда выполнены при
соседнем кодировании любые два состояния,
связанные дугой на графе автомата,
кодируются наборами ,отличающимися
состояниями лишь одного эл. Памяти .
Соседнее кодирование возможно не всегда
. Граф автомата , допускающего соседнее
кодирование должен удовлетворять ряду
требований : 1- в графе автомате не должно
быть циклов с не четным числом вершин
2- два соседних состояния второго порядка
не должны иметь более двух состояний
, лежащих между ними. Под состояниями
второго порядка понимаются такие два
состояния , путь между которыми по графу
автомата состоит из двух ребер не
зависимо от ориентации . при соседнем
кодировании обычно пользуются картой
Карно . В этом случае состояние , связанное
дугой , располагают на соседних клетках
карты. При соседнем кодировании на
каждом переходе переключается только
один триггер, что принципиально устраняет
гонки. Анализ метода структурного
синтеза автомата показывает ,что
различные варианты кодирования состояния
автомата приводят к различным выражениям
функции возбуждения памяти и ф-ии выхода
, в результате чего сложность комбинационной
схемы существенно зависит от выбранного
кодирования . Среди множества алгоритмов
кодирования имеются два наиболле часто
встречающихся 1- алгоритм кодирования
для D-
триггеров ,2- эвристический алгоритм
кодирования. Алгоритм кодирования для
D-
триггеров : при кодировании не обходимо
выполнить следующее 1- каждому состоянию
автомата
 ставится
в соответствие целое число
ставится
в соответствие целое число
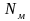 , равное числу переходов состояний
(
=числу
появлений
, равное числу переходов состояний
(
=числу
появлений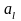 в
поле таблицы переходов или числу дуг
, входящих в
при графическом способе задания автомата
) 2-числа
в
поле таблицы переходов или числу дуг
, входящих в
при графическом способе задания автомата
) 2-числа
 ,
, ,
, и так далее
упорядочиваются по убыванию . 3- состояние
и так далее
упорядочиваются по убыванию . 3- состояние
 с наибольшим числом
с наибольшим числом
 кодируется
следующим образом (000…..0) –R,R-
Количество эл. Памяти . 4- Следующее R
состояние кодируется кодами , содержащими
только одну единицу для оставшихся
состояний в порядке списка из второго
пункта используют коды с двумя ед. ,
затем с тремя и т.д., пока не будут
закодированы все состояния . В результате
получается такое кодирование, при
котором чем больше имеется переходов
в не которое состояние тем меньше ед.
в коде .Так как для D-
триггеров ф-.ии возбуждения однозначно
определяются кодом состояния перехода
, очевидно что выражение для ф-ии
возбуждения будут проще. Этот метод
особенно эффективен при отсутствии
минимальной ф-ии возбуждения, что имеет
место в реальных автоматах с большим
количеством внутренних состояний и
вх. Переменных. Аналогично кодирование
вн. Состояний для D-
триггеров можно кодировать в выходные
сигналы для любого типа триггеров ,
т.е. чем чаще выбирается данный выходной
сигнал , тем меньше ед. в его коде .
кодируется
следующим образом (000…..0) –R,R-
Количество эл. Памяти . 4- Следующее R
состояние кодируется кодами , содержащими
только одну единицу для оставшихся
состояний в порядке списка из второго
пункта используют коды с двумя ед. ,
затем с тремя и т.д., пока не будут
закодированы все состояния . В результате
получается такое кодирование, при
котором чем больше имеется переходов
в не которое состояние тем меньше ед.
в коде .Так как для D-
триггеров ф-.ии возбуждения однозначно
определяются кодом состояния перехода
, очевидно что выражение для ф-ии
возбуждения будут проще. Этот метод
особенно эффективен при отсутствии
минимальной ф-ии возбуждения, что имеет
место в реальных автоматах с большим
количеством внутренних состояний и
вх. Переменных. Аналогично кодирование
вн. Состояний для D-
триггеров можно кодировать в выходные
сигналы для любого типа триггеров ,
т.е. чем чаще выбирается данный выходной
сигнал , тем меньше ед. в его коде .
38. Микропрограммирование. Операционный и управляющий автомат.В ЭВМ д\выполнения операций используются операционные устройства, каналы ввода-вывода, контроллеры, процессоры, к-ые в процессе работы осуществляют преобразование их входных сигналов в выходные по некоторому закону. Организация этих устройств основана на принципе микропрограммного управления, который заключается в следующем: 1. любая операция, реализуемая устройством, рассматривается, как сложное действие, которое разбивается на последовательность элементарные действий над словами информации. Эти элем-ые действия называются микрооперациями, к ним относятся передача информации из одного регистра в другой, взятие обратного входа, сдвиг, суммирование, инверсия и т.д. 2. Для управления порядком следования микроопераций используются логические условия, которые в зависимости от значений слов преобразованных микроопераций принимают значения «ложь или истина». 3. Процесс выполнения операций в устройстве описывается в форме алгоритма, который представляется в терминах микроопераций и логических условий, и называется микропрограммой. Микропрограмма определяет порядок проверки логических условий и следования микрооперации, необходимые для получения требуемых результатов. 4. На основе микропрограммы определяется структура и порядок функционирования устройства во времени. В любом устройстве в обработке цифровой операции можно выделить два блока операций: операционный авт-т и управляющий.
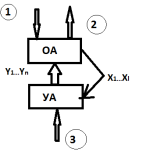 1-входные
слова;2-выходные слова;3-коды.операций;
1-входные
слова;2-выходные слова;3-коды.операций;
 Операционный
авт-т хранит слова операции, выполняет
набор микроопераций, вычисляет значения
логических условий, т.е. только хранит
и обрабатывает данные. Для работы
операционного авт-та используется
входные слова, вводимые в авт-т в качестве
операндов. Авт-т формирует выходные
слова, являющиеся результатами операции.
В процессе работы операционный авт-т
может использовать внутренние слова,
например, const
или слова для хранения вспомогательных
опрераций. Операционный авт-т может
выполнять микрооперации и вычислять
логические условия, но не определяет
порядок следования этих действий во
времени, т.е. операционный авт-т
характеризует свойства, которые могут
быть использованы для вычислений, но
не сам вычислительный процесс. Порядок
выполнения действий во времени в опер-ом
авт-те обусловлен алгоритмом выполнения
операций задает управляющий авт-т. Он
генерирует последовательность
управляющих сигналов для операционного
авт-та. С каждым упр-им сигналом связана
одна микрооперация. Значения логических
условий, вычисленных в операционном
авт-те, передаются в управляющий авт-т,
т.о. в упр-ий авт-т поступают коды
операций, которые нужно выполнить в
устройстве и коды логических условий
из операционного авт-та. Т.о. любое
операционное устройство является
композицией операционного и управляющего
авт-та. Опер-ый авт-т реализует действие
над словами информации, является
исполнительной частью устройства,
работой которого управляет упр-ий
авт-т. Генерирующие необходимые
последовательности управляющих
сигналов. Порядок выполнения действий
во времени задается операторной схемой
алгоритма (микропрограмма) ,которая
обычно представляется в виде граф-схемы
алгоритма.
Операционный
авт-т хранит слова операции, выполняет
набор микроопераций, вычисляет значения
логических условий, т.е. только хранит
и обрабатывает данные. Для работы
операционного авт-та используется
входные слова, вводимые в авт-т в качестве
операндов. Авт-т формирует выходные
слова, являющиеся результатами операции.
В процессе работы операционный авт-т
может использовать внутренние слова,
например, const
или слова для хранения вспомогательных
опрераций. Операционный авт-т может
выполнять микрооперации и вычислять
логические условия, но не определяет
порядок следования этих действий во
времени, т.е. операционный авт-т
характеризует свойства, которые могут
быть использованы для вычислений, но
не сам вычислительный процесс. Порядок
выполнения действий во времени в опер-ом
авт-те обусловлен алгоритмом выполнения
операций задает управляющий авт-т. Он
генерирует последовательность
управляющих сигналов для операционного
авт-та. С каждым упр-им сигналом связана
одна микрооперация. Значения логических
условий, вычисленных в операционном
авт-те, передаются в управляющий авт-т,
т.о. в упр-ий авт-т поступают коды
операций, которые нужно выполнить в
устройстве и коды логических условий
из операционного авт-та. Т.о. любое
операционное устройство является
композицией операционного и управляющего
авт-та. Опер-ый авт-т реализует действие
над словами информации, является
исполнительной частью устройства,
работой которого управляет упр-ий
авт-т. Генерирующие необходимые
последовательности управляющих
сигналов. Порядок выполнения действий
во времени задается операторной схемой
алгоритма (микропрограмма) ,которая
обычно представляется в виде граф-схемы
алгоритма.
39.Граф-схемы
алгоритмов (ГСА)Порядок
выполнения действий во времени задается
операторной схемой алгоритма
(микропрограмма),которая обычно
представляется в виде граф-схемы
алгоритма . ГСА определяет вычислительный
процесс последовательно во времени ,
устанавливая порядок логических условий
и порядок следования микроопераций .В
ГСА используются вершины следующих
типов 1- вершина начала , имеет один
выход , вх. Нет, обозначает начало
микропрограммы. 2-Вершина – конец имеет
любое число входов, вых. Нет , обозначает
конец микропрограммы . 3- Операторная
вершина имеет любое число вх. , один
вых.; внутри операторной вершины
записывается одна микрокоманда , а
именно савокупность микроопераций ,
допускающих совместное выполнение 4-
условная вершина имеет любое число
вх. И два выхода ;Внутри условной вершины
записывается булевое выражение , в
зависимости от значений которого
осуществляется выбор дальнейшего
направления выполнения микропрограммы
5- особый вид – условные вершины –
ждущая вершина имеет множество вх. ,
два выхода , но один из них заведен на
вход. При попадании в ждущую вершину
выход из нее возможен только при
выполнении условия Х .
![]()
![]()
![]()
![]()
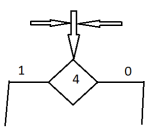 Граф
микропрограммы состоит из совокупности
вершин и дуг, соединенных выходами один
вершин с входами др. вершин. ГСА называется
содержательным, если внутри вершин в
явном виде записаны микрооперации и
логические условия.
Граф
микропрограммы состоит из совокупности
вершин и дуг, соединенных выходами один
вершин с входами др. вершин. ГСА называется
содержательным, если внутри вершин в
явном виде записаны микрооперации и
логические условия.
40.
Переход от ГСА к автоматному описанию.
Граф микропрограммы состоит из
совокупности вершин и дуг, соединенных
выходами один вершин с входами др.
вершин. ГСА называется содержательным,
если внутри вершин в явном виде записаны
микрооперации и логические условия.
Если каждую микрооперацию обозначить
символом
 ,
логические условия через
,
логические условия через
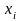 ,
то получится кодированная граф схема
авт-та. Различные микрооперации вып-ся
операционными элементами, которые
явл-ся составными частями основного
операционного авт-та. Под операционным
элементом понимаются устройства,
реализующие одну из следующих функций
или их произвольную комбинацию. Хранение
слова информаций, выполнение некоторых
микроопераций, в результате которых
вычисляются новое значение слова.
Вычисление логического условия,
зависящего от слова. Для построения
операционного авт-та операционные
элементы соединяются между собой с
помощью цепей передачи слов информации
от выходов одних элементов к входам
других. В зависимости от выполненных
микроопераций операционные эл-ты
делятся на разновидности: шина, регистр,
счетчик, сумматор, схема сравнения,
дешифратор, шифратор и т.д. Для различных
содержательных ГСА операционные авт-ты
будут различны, но управление авт-та
будет одним и тем же. Конечный авт-т,
интерпретирующий микропрограммы работы
дискретного устройства, назначается
микропрограммой авт-та. Одну и ту же
ГСА можно интерпретировать, как автоматом
Мили, так и авт-ом Мура. Абстрактный
синтез микропр-ого авт-та по ГСА
осуществляется в два этапа: 1. получение
отмеченной ГСА; 2. постороение графа
авт-та и таблицы переходов и выходов.
,
то получится кодированная граф схема
авт-та. Различные микрооперации вып-ся
операционными элементами, которые
явл-ся составными частями основного
операционного авт-та. Под операционным
элементом понимаются устройства,
реализующие одну из следующих функций
или их произвольную комбинацию. Хранение
слова информаций, выполнение некоторых
микроопераций, в результате которых
вычисляются новое значение слова.
Вычисление логического условия,
зависящего от слова. Для построения
операционного авт-та операционные
элементы соединяются между собой с
помощью цепей передачи слов информации
от выходов одних элементов к входам
других. В зависимости от выполненных
микроопераций операционные эл-ты
делятся на разновидности: шина, регистр,
счетчик, сумматор, схема сравнения,
дешифратор, шифратор и т.д. Для различных
содержательных ГСА операционные авт-ты
будут различны, но управление авт-та
будет одним и тем же. Конечный авт-т,
интерпретирующий микропрограммы работы
дискретного устройства, назначается
микропрограммой авт-та. Одну и ту же
ГСА можно интерпретировать, как автоматом
Мили, так и авт-ом Мура. Абстрактный
синтез микропр-ого авт-та по ГСА
осуществляется в два этапа: 1. получение
отмеченной ГСА; 2. постороение графа
авт-та и таблицы переходов и выходов.
41.
Разметка ГСА по моделям Мили и Мура.Под
разметкой ГСА понимается процесс
сопоставления оператором граф-схемы
символов состояний и выходов автоматной
модели Мура или Мили. В результате такой
разметки и дальнейшего преобразования
должен получиться граф состояний и
переходов авт-та Мура или Мили
соответственно. Для авт-та Мура выходной
сигнал является функцией только
внутреннего состояния и не зависит от
входного сигнала, поэтому каждую
операторную вершину ГСА следует пометить
символом определенного состояния
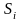 ,
которому можно приписать определенное
значение выхода
,
которому можно приписать определенное
значение выхода
 ,
т.о. будут определены вершины состояний
/
в
графе авт-та Мура. Все возможные пути
через условные вершины к оператору в
ГСА будут отражены в виде граф дуг
переходов в графе авт-та Мура. Этим
дугам следует приписать входные сигналы
,
т.о. будут определены вершины состояний
/
в
графе авт-та Мура. Все возможные пути
через условные вершины к оператору в
ГСА будут отражены в виде граф дуг
переходов в графе авт-та Мура. Этим
дугам следует приписать входные сигналы
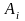 ,
являющиеся конъюнкциями логических
условий
,
являющиеся конъюнкциями логических
условий
 в ГСА. Переход авт-та из одного состояния
в другое при отсутствии логических
условий происходит под воздействием
синхросигнала. К модели авт-та Мили
достаточно просто перейти, используя
определенные правила. Построение модели
Мили в некоторых случаях может привести
к сокращению числа внутренних состояний
авт-та. Однако модель Мура более
естественным образом вытекает из ГСА,
поэтому целесообразно ориентироваться
на построение этой модели.Синтез
авт-та Мили по ГСА.
На этапе получения отмеченной ГСА входы
вершин, следующих за операторными,
отмечаются символами
в ГСА. Переход авт-та из одного состояния
в другое при отсутствии логических
условий происходит под воздействием
синхросигнала. К модели авт-та Мили
достаточно просто перейти, используя
определенные правила. Построение модели
Мили в некоторых случаях может привести
к сокращению числа внутренних состояний
авт-та. Однако модель Мура более
естественным образом вытекает из ГСА,
поэтому целесообразно ориентироваться
на построение этой модели.Синтез
авт-та Мили по ГСА.
На этапе получения отмеченной ГСА входы
вершин, следующих за операторными,
отмечаются символами
 …..по
следующим правилам: 1символом
…..по
следующим правилам: 1символом
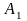 отмечают
вход вершины, следующей за начальной,
а так же вход конечной вершины.2Входы
всех вершин, следующих за операторными,
должны быть отмечены.3Входы
различных вершин, за исключением
конечной, отмечаются различными
символами .4вход
вершины отмечается только одним
символом. .
Результатом первого этапа явл-ся
отмеченная ГСА, которая служит основой
для 2этапа перехода графов или таблиц
переходов выходов.На втором этапе из
отмеченной ГСА строят граф авт-т или
таблицу переходов выходов. Для этого
полагают, что в авт-те будет столько
состояний, сколько символов
понадобилось при отметке ГСА. На
плоскости отмечаются все состояния
авт-та
,
для каждого из них определяют по
отмеченной ГСА все пути, ведущие в
другие состояния и проходящие обязательно
только через одну операторную вершину.
На графе отмечаются все указанные пути
для всех состояний в виде дуг, которым
приписываются условия перехода и
выходной сигнал, выработанный на этом
переходе, в результате получается граф
авт-т Мили. На основании отмеченной ГСА
или графа авт-та можно построить таблицы
переходов выходов. Для микропрограммных
авт-ов таблица переходов выходов
строится в виде списка. Различаются
прямая и обратная таблицы.Синтез
ав-та Мура по ГСА.
Для авт-та Мура на этапе получения
отмеченной ГСА разметка производится
согласно следующим правилам:1. Символом
отмечается начальная и конечная вершины
ГСА;2.Различные операторные вершины
отмечаются различными символами; 3. Все
операторные вершины должны быть
отмечены, после того строят таблицы
переходов и выходов. Обычно для авт-та
Мура в таблицах переходов и выходов не
исп-ся дополнительный столбец для
выходных сигналов. Выходные сигналы
записываются в столбце, где указывается
исходное состояние или состояние
перехода
отмечают
вход вершины, следующей за начальной,
а так же вход конечной вершины.2Входы
всех вершин, следующих за операторными,
должны быть отмечены.3Входы
различных вершин, за исключением
конечной, отмечаются различными
символами .4вход
вершины отмечается только одним
символом. .
Результатом первого этапа явл-ся
отмеченная ГСА, которая служит основой
для 2этапа перехода графов или таблиц
переходов выходов.На втором этапе из
отмеченной ГСА строят граф авт-т или
таблицу переходов выходов. Для этого
полагают, что в авт-те будет столько
состояний, сколько символов
понадобилось при отметке ГСА. На
плоскости отмечаются все состояния
авт-та
,
для каждого из них определяют по
отмеченной ГСА все пути, ведущие в
другие состояния и проходящие обязательно
только через одну операторную вершину.
На графе отмечаются все указанные пути
для всех состояний в виде дуг, которым
приписываются условия перехода и
выходной сигнал, выработанный на этом
переходе, в результате получается граф
авт-т Мили. На основании отмеченной ГСА
или графа авт-та можно построить таблицы
переходов выходов. Для микропрограммных
авт-ов таблица переходов выходов
строится в виде списка. Различаются
прямая и обратная таблицы.Синтез
ав-та Мура по ГСА.
Для авт-та Мура на этапе получения
отмеченной ГСА разметка производится
согласно следующим правилам:1. Символом
отмечается начальная и конечная вершины
ГСА;2.Различные операторные вершины
отмечаются различными символами; 3. Все
операторные вершины должны быть
отмечены, после того строят таблицы
переходов и выходов. Обычно для авт-та
Мура в таблицах переходов и выходов не
исп-ся дополнительный столбец для
выходных сигналов. Выходные сигналы
записываются в столбце, где указывается
исходное состояние или состояние
перехода
 .
Получением графа или таблицы переходов
или выходов заканчивается этап
абстрактного синтеза микропрограммного
авт-та.
.
Получением графа или таблицы переходов
или выходов заканчивается этап
абстрактного синтеза микропрограммного
авт-та.
42. Методы адресации в микропроцессорных аппаратах.Устройство управления микропрограммным автоматом.Задачей устройства управления является, во-1, управление последовательностью микроопераций в АЛУ и в ОЗУ, во-2, управление последовательностью собственных микроопераций. Для установления набора микроопераций УУ зафиксируем, прежде всего, количество и характер работы используемых в нем регистров.Важнейшим из регистров УУ (и всего автомата в целом) является так называемый регистр команд (РК). Для трехадресных команд этот регистр «условно» можно разделить на четыре регистра:− регистр операций (РО), регистрирующий (запоминающий) код операции выполняемой команды;− регистры первого, второго и третьего адреса (РА1, РА2, РА3), которые позволяют запомнить соответственно первый, второй и третий адреса, необходимые выполняемой команде.Другой важной составной частью УУ является счетчик команд (СК), предназначенный для хранения адреса ячейки ОЗУ, из которой должна извлекаться очередная команда программы. Наконец, имеется еще регистр микроопераций (РМО), заменяемый иногда счетчиком микротактов (СМТ).Счетчик микротактов реализуется всегда как циклический (замкнутый) счетчик, что же касается счетчика команд, то он может быть и незамкнутым. Как следует из общего принципа программного управления, чтобы обеспечить управление работой всех устройств (включая и само устройство), УУ должно осуществлять автоматическую выборку команд из ОЗУ, а также их расшифровку и выполнение. С этой целью в набор микроопераций УУ должны быть включены следующие микрооперации:1) передача кода (программного слова) из регистра числа ОЗУ на регистр команд;2) передача первого адреса из РА в регистр адреса ОЗУ;3) передача второго адреса из РА в регистр адреса ОЗУ;4) передача третьего адреса из РА в регистр адреса ОЗУ;5) посылка импульса в счетчик команд (увеличение номера команды на 1);6) очистка регистра команд и регистра микроопераций;7) передача третьего адреса из РА в счетчик команд;8) передача содержимого счетчика команд в регистр адреса ОЗУ.Восьмая микрооперация дает возможность реализовать операцию условного перехода.Для организации управления последовательностью микроопераций строитсяКА М с регистровой памятью в виде регистра микроопераций. Выходные сигналы этого автомата представляют собой импульсы управления микрооперациями, посылаемые по одному или одновременно по нескольким из каналов управления микрооперациями (с изменением набора микроопераций меняется вообще говоря,и число этих каналов).На вход автомата М поступают входные сигналы (сигналы обратной связи, подаваемые из АЛУ), представляющие собой выходные сигналы триггеров регистра операций (операционные входы). Кроме того, имеется один импульсный тактирующий вход, задающий тактировку (разбиение времени на микротакты) автомата М и всего универсального программного автомата в целом. Для синхронного автомата импульсные тактирующие сигналы вырабатываются специальным синхронизирующим генератором, работающим с постоянной частотой. Можно построить автомат М как асинхронный автомат, тогда после выдачи выходного сигнала для выполнения очередной микрооперации автомат переходит в состояние ожидания ответного сигнала от соответствующего устройства, свидетельствующего об окончании выполнения этой микрооперации. Ответные сигналы и будут играть роль тактирующего сигнала. Длительность микротактов при этом будет неодинаковой.Задача организации управления микрооперациями любого универсального программного автомата Q есть задача синтеза соответствующего автомата М, который будет называться микропрограммным блоком.Формирование адреса микрокоманд. Принудительная и естественная адресация.В автоматах с программируемой логикой микрокоманды содержат адресную часть, позволяющую определять номера ячеек ПЗУ, к которым обращаются адресуемые микрокоманды. Способ адресации микрокоманд задает правило определения адреса следующей микрокоманды. Используются два основных способа адресации:принудительная и естественная адресация.Принудительная адресация сводится к указанию в каждой микрокоманде адреса следующей микрокоманды. Этот способ реализован в управляющем автомате, который работает по микропрограмме, представляющей собой последовательность микрокоманд.Данная структура микрокоманды в каждом такте может выполнять не более одной микрооперации.После выполнения микрооперации осуществляется переход к следующей микрокоманде, адрес которой определяется полем А0 или А1 в зависимости от значения поля Х и логических условий х1,…, хL, формируемых в операционном автомате.Если Х ≠ 0, то адрес А назначается равным А0 или А1 в зависимости от значения Хх, выделенного полем Х : А = А0, если Хх = 0 или А = А1, если Хх = 1. Условно считается, что логическое условие х0 тождественно нулю. Поэтому при Х = 0 адрес А = А0. Это правило вычисления адреса следующей микрокоманды реализуется схемой, состоящей из дешифратора ДШХ, подсхемы И-ИЛИ и элемента НЕ, на выходе которых формируются управляющие сигналы а0 и а1, инициирующие передачуА := А0 и А := А1 соответственно.Таким образом, к окончанию такта на адресной шине А будет сформирован адрес следующей микрокоманды, выбираемой из ПЗУ в очередном такте.Перед началом работы управляющего автомата регистр микрокоманды МК устанавливается в нулевое положение, в результате чего адрес А = 0 и первой будет выбрана микрокоманда, хранимая в нулевой ячейке ПЗУ.Запуск автомата приводится сигналом В, который переключит триггер Т в состояние 1, в результате чего синхронизирующий сигнал С поступает на управляющий вход ЧТ, возбуждая в каждом такте процесс чтения микрокоманды из ПЗУ. В последнем такте реализации микропрограммы триггер Т должен быть переключен в состояние 0Для этого в системе микроопераций вводится дополнительная микрооперация Ум+1, которая интерпретируется в виде сигнала F, останавливающего работу управляющего автомата.При естественной адресации адрес следующей микрооперации принимают равным увеличенному на единицу адресу предыдущей микрокоманды, т. е. если А – адрес выполняемой микрокоманды, то следующая микрокоманда выбирается из ячейкис адресом (А + 1).Естественный способ адресации не требует введения адресного поля в каждуюмикрокоманду. Если микрокоманды следуют в естественном порядке, а процесс адресации реализуется счетчиком адреса микрокоманды, состояние которого увеличивается на единицу после чтения очередной микрокоманды. Следовательно, микрокоманды, которые задают функциональные преобразования, состоящие из набора микроопераций могут содержать только операционную часть с полями Y1, Y2, …, YМ.После выполнения микрокоманды с адресом А может возникнуть необходимость в переходе к микрокоманде с адресом В ≠ А+1. Переход может быть безусловным или зависеть от текущего значения Хх. Условные переходы реализуются следующим образом:если Хх = 0, то выполняется следующая микрокоманда с адресом (А+1);если Хх = 1, то следующей выполняется микрокоманда с адресом В.При естественной адресации обычно используются микрокоманды двух типов:операционные и управляющие.Операционная микрокоманда задает набор микроопераций Y1,Y2,… ,YМ и указывает на адрес следующей микрокоманды, равный (А+1). Управляющие микрокоманды используются для изменения естественного порядка следования микрокоманд, что сводится к выполнению безусловных и условных переходов. Управляющая микрокоманда содержит поле Х, определяющее номер логического условия, и поле В, определяющее адрес следующей микрокоманды. Если Х = 0, то адрес следующей микрокоманды безусловно равен В. Для выделения операционных и управляющих микрокоманд в управляющем слове вводится одноразрядное поле признака Р, определяющего тип микрокоманды: если Р = 0, то микрокоманда является операционной;если Р = 1 – управляющей. Возможная структура рассмотренных управляющих слов
45.программирование ПЛК Simantik s7-200.основные редакторыПрограммирование ПЛК SIMATIC S7-200 осуществляется с помощью пакета STEP 7 Micro/Win. В пакете реализована поддержка языков LAD (релейно-контактные схемы), STL (список инструкций) и FBD (функц блоков диаграмм). Связь компьютера с программируемым ЦП осуществляется через PC/PPI-кабель. STEP 7 Micro/Win позволяет выполнять все операции по программированию контроллеров SIMATIC S7-200.Основная работа S7-200 CPU:-CPU считывает состояние входов.-Программа, хранимая в CPU, использует эти входы для вычисления логики управления. Во время выполнения программы CPU обновляет данные.-CPU записывает данные в выходы.Программа S7-200 делится на след организационные элементы:Глав программа: Основная часть программы, где размещаются команды, управляющие вашим приложением. Команды главной программы выполняются последовательно и однократно в каждом цикле сканирования CPU.-Программы обработки прерываний: Эти необязательные элементы программы выполняются при каждом возникновении события, вызывающего прерывание.-Подпрограммы: Эти необязательные элементы программы выполняются только тогда, когда они вызываются из главной программы или программы обработки прерываний.CPU выполняет все или большинство из следующих задач:• считывание входов• выполнение программы(В фазе выполнения цикла сканирования CPU выполняет программу, начиная с первой команды и продолжая до конечной команды)• обработка любых коммуникационных запросов(Во время фазы обработки сообщений в цикле сканирования CPU обрабатывает любые сообщения, принятые из коммуникационного порта)• выполнение самодиагностики CPU(проверяет свое встроенное программное обеспечение и память вашей программы (только режим RUN). Он проверяет также состояние всех модулей ввода-вывода)• запись в выходы(В конце каждого цикла сканирования CPU записывает значения, хранимые в регистре выходов образа процесса, в цифровые выходы).CPU 7-200 имеет два режима работы:• STOP: CPU не выполняет программу. Когда CPU находится в режиме STOP, вы можете загружать программу или конфигурировать CPU.• RUN: CPU выполняет программу.Светодиод состояния на лицевой стороне CPU показывает текущий режим работы.редакторы программирования контроллеров S7 200Редактор списка команд (STL) STEP 7-Micro/WIN 32 позволяет создавать управл программы, вводя мнемонику команд.
 CPU
выполняет команды в порядке, предписанном
программой, сверху донизу и затем опять
начинает сверху. Основные особенности:-STL
лучше всего подходит опытным
программистам.-STL иногда позволяет
решать проблемы, которые невозможно
достаточно легко решить при помощи
редактора LAD или FBD.-Использовать редактор
STL возможно только с системой команд
SIMATIC.-Всегда возможно использовать
редактор STL для просмотра или редактирования
программы, созданной с помощью редактора
SIMATIC LAD или FBD, обратное не всегда
возможно.Редактор
контактного плана (LAD)
STEP 7-Micro/WIN 32 позволяет формировать
программы, имеющие сходство с электрической
монтажной схемой. Программа выполняется
по “цепям” слева направо и затем сверху
вниз, как предписано программой. Как
только CPU достигает конца программы,
он начинает снова с вершины программы.
Контакты представляют логические
состояния “входов”, аналогичных
выключателям, кнопкам, внутренним
условиям и так далее.Катушки обычно
представляют логические результаты
“выходов”, аналогичных лампам,
пускателям электродвигателей,
промежуточным реле, состояниям внутренних
выходов и так далее.Блоки представляют
дополнительные команды, такие как
таймеры, счетчики или математические
команды.Основные
особенности,
-Контактный план прост в использовании
для начинающих программистов.-Графическое
представление часто более легко
понимается и является популярным во
всем мире.Редактор LAD можно использовать
и с системой команд SIMATIC, и с системой
команд IEC 1131–3.-Для отображения программы,
созданной при помощи редактора SIMATIC
LAD, всегда можно использовать редактор
STL.Редактор
функционального плана
(FBD) STEP 7-Micro/WIN 32 позволяет просматривать
команды в форме логических блоков,
напоминающих логические блок-схемы
общего вида. имеются эквивалентные
команды, которые появляются как команды
в форме блоков.выход одной команды
может использоваться для того, чтобы
разрешить другой команде создать
необходимую логику управления. Основные
особенности:-Графический стиль
представления в форме логических
элементов хорош для последующего
составления блок-схемы программы.-Редактор
FBD можно использовать и с системой
команд SIMATIC, и с системой команд IEC
1131–3.- Для отображения программы,
созданной при помощи редактора SIMATIC
FBD, всегда можно использовать редактор
STL.
CPU
выполняет команды в порядке, предписанном
программой, сверху донизу и затем опять
начинает сверху. Основные особенности:-STL
лучше всего подходит опытным
программистам.-STL иногда позволяет
решать проблемы, которые невозможно
достаточно легко решить при помощи
редактора LAD или FBD.-Использовать редактор
STL возможно только с системой команд
SIMATIC.-Всегда возможно использовать
редактор STL для просмотра или редактирования
программы, созданной с помощью редактора
SIMATIC LAD или FBD, обратное не всегда
возможно.Редактор
контактного плана (LAD)
STEP 7-Micro/WIN 32 позволяет формировать
программы, имеющие сходство с электрической
монтажной схемой. Программа выполняется
по “цепям” слева направо и затем сверху
вниз, как предписано программой. Как
только CPU достигает конца программы,
он начинает снова с вершины программы.
Контакты представляют логические
состояния “входов”, аналогичных
выключателям, кнопкам, внутренним
условиям и так далее.Катушки обычно
представляют логические результаты
“выходов”, аналогичных лампам,
пускателям электродвигателей,
промежуточным реле, состояниям внутренних
выходов и так далее.Блоки представляют
дополнительные команды, такие как
таймеры, счетчики или математические
команды.Основные
особенности,
-Контактный план прост в использовании
для начинающих программистов.-Графическое
представление часто более легко
понимается и является популярным во
всем мире.Редактор LAD можно использовать
и с системой команд SIMATIC, и с системой
команд IEC 1131–3.-Для отображения программы,
созданной при помощи редактора SIMATIC
LAD, всегда можно использовать редактор
STL.Редактор
функционального плана
(FBD) STEP 7-Micro/WIN 32 позволяет просматривать
команды в форме логических блоков,
напоминающих логические блок-схемы
общего вида. имеются эквивалентные
команды, которые появляются как команды
в форме блоков.выход одной команды
может использоваться для того, чтобы
разрешить другой команде создать
необходимую логику управления. Основные
особенности:-Графический стиль
представления в форме логических
элементов хорош для последующего
составления блок-схемы программы.-Редактор
FBD можно использовать и с системой
команд SIMATIC, и с системой команд IEC
1131–3.- Для отображения программы,
созданной при помощи редактора SIMATIC
FBD, всегда можно использовать редактор
STL.
46. CPU s7-200.адресация Используя байтовый формат адреса можно обращаться к данным в различных областях памяти CPU (V, I, Q, M, S, L и SM) как к байтам, словам или двойным словам. Для доступа к байту, слову или двойному слову в памяти CPU нужно указать адрес, таким же способом, как и при указании адреса бита. Он включает идентификатор области, обозначение размера данных и начальный байтовый адрес байта, слова или двойного слова. Доступ к данным в других областях памяти CPU (таким, как T, C, HC и аккумуляторы) производится с помощью формата адреса, включающего идентификатор области и номер элемента.Адресация регистра входов образа процесса (I)можно получить доступ к регистру входов образа процесса в битах, байтах, словах или двойных словах.Формат:Бит I[адрес байта].[адрес бита] I0.1Байт, слово, двойное слово I[размер][начальный адрес байта] IB4Адресация регистра выходов образа процесса (Q)В конце цикла CPU копирует значения, хранящиеся в регистре выходов образа процесса в физические выходы. Формат:Бит Q[адрес байта].[ адрес бита] Q1.1Байт, слово, двойное слово Q[размер][ начальный адрес байта] QB5Адресация области памяти переменных (V) можно использовать V-память для хранения промежуточных результатов операций, выполняемых в программе управляющей логикой. можно также использовать V-память для хранения других данных, относящихся к вашему процессу или задаче. Вы можете получить доступ к V-памяти в битах, байтах, словах или двойных словах.Формат:Бит V[адрес байта].[адрес бита] V10.2;Байт, слово, двойное слово V[размер][начальный адрес байта];VW100Адресация битовой памяти (маркеров) (M)можно использовать область битовой памяти (M-память) в качестве управляющих реле для хранения промежуточного состояния операции или другой управляющей информации. Хотя название “область битовой памяти” подразумевает, что информация хранится в единицах длиной в бит, вы можете получить доступ к области битовой памяти не только в битах, но также и в байтах, словах или двойных словах.Формат:Бит M[адрес байта].[адрес бита] M26.7;Байт, слово, двойное слово M[размер][начальный адрес байта]MD20Адресация области памяти реле управления последовательностью операций (S)Биты реле управления последовательностью операций (S) используются для организации машинных операций или шагов в эквивалентные сегменты программы. Реле управления последовательностью операций делают возможной сегментацию программы управления. Вы можете получить доступ к области S в битах, байтах, словах или двойных словах.Формат:Бит S[адрес байта].[адрес бита] S3.1;Байт, слово, двойное слово S[размер][начальный адрес байта] SB4.Адресация битов специальной памяти (SM)SM-биты предоставляют средства для обмена информацией между CPU и вашей программой. Вы можете использовать эти биты для выбора и управления некоторыми специальными функциями CPU S7–200, такими, как:-бит, устанавливающийся при первом цикле обработки программы,-бит, переключающийся с определенной частотой,- биты, показывающие состояние арифметических или операционных команд.Хотя SM-область основана на битах, вы можете получить обращаться к данным в этой области как к битам, байтам, словам или двойным словам.Формат:Бит SM[адрес байта].[адрес бита] SM0.1:Байт, слово, двойное слово SM[размер][начальный адрес байта] SMB86.Адресация области локальной памяти (L)ПЛК S7–200 предоставляет 64 байта локальной памяти (L), из которых 60 могут быть использованы в качестве сверхоперативной памяти или для передачи формальных параметров подпрограммам. Если вы программируете на LAD (КОР) или FBD (FUP), то STEP 7-Micro/WIN 32 резервирует последние 4 байта локальной памяти для собственных целей. Если вы программируете на STL (AWL), то доступны все 64 байта L-памяти, но не рекомендуется использовать последние четыре байта этой памяти.Локальная память похожа на V-память за одним существенным исключением. V-память имеет глобальную сферу действия, тогда как L-память имеет локальную сферу действия. Термин глобальная сфера действия означает, что одна и та же ячейка памяти доступна из любого программного объекта (главной программы, подпрограмм или программ обработки прерываний). Термин локальная сфера действия означает, что распределение памяти ассоциируется с конкретным программным объектом. ПЛК S7–200 выделяют 64 байта L-памяти для главной программы, 64 байта для каждого уровня вложенности подпрограмм и 64 байта для программ обработки прерываний. L-память, выделенная для главной программы, недоступна из подпрограмм или программ обработки прерываний. Подпрограмма не может получить доступ к L-памяти, выделенной для главной программы, программы обработки прерывания или другой подпрограммы. Аналогично, программа обработки прерывания не может получить доступ к L-памяти, выделенной для главной программы или подпрограммы. Выделение L-памяти производится ПЛК S7–200 по принципу «сколько нужно». Это значит, что пока выполняется главная часть программы, выделение L-памяти для подпрограмм и программ обработки прерываний не производится. При возникновении прерывания или вызове подпрограммы выделяется требуемое количество локальной памяти. Новое выделение L-памяти может повторно использовать ячейки L-памяти другой подпрограммы или программы обработки прерывания. L-память не инициализируется ПЛК при ее выделении и может содержать любое значение. Когда вы передаете формальные параметры в вызов подпрограммы, значения передаваемых параметров помещаются CPU в соответствующие ячейки L-памяти вызываемой подпрограммы. Ячейки L-памяти, которые не получают значения при передаче формальных параметров не будут инициализированы и могут содержать во время выделения памяти любое значение. Вы можете получить доступ к L-памяти в виде битов, байтов, слов или двойных слов. Вы можете использовать L-память как указатель для косвенной адресации, но вы не можете косвенно обращаться к L-памяти.Формат:Бит L [адрес байта].[адрес бита] L0.0,Байт, слово, двойное слово L [размер] [начальный адрес байта] LB33
47таймеры циклический сдвиг. Таймер с задержкой включения, таймер с задержкой включения с запоминанием, таймер с задержкой выключения Команды. Таймер с задержкой включения (TON) и Таймер с задержкой включения с запоминанием (TONR) отсчитывают время, когда включен разрешающий вход. Когда текущее значение (Txxx) становится > или = предустановл времени (PT), бит таймера устанавливается. Текущее значение Таймера с задержкой включения сбрасыв, когда выкл разрешающ вх, тогда как текущее значение Таймера с задержкой включения с запоминанием сохраняется, когда этот вход выкл. Вы можете использовать Таймер с задержкой включения с запоминанием для накопления времени за несколько периодов, когда включен разрешающ вход. Для стирания текущего значения Таймера с задержкой включения с запоминанием используется команда Сброс (R).Таймер с задержкой включения и Таймер с задержкой включения с запоминанием продолжают счет после достижения предустановленного значения, они останавливают счет при достижении максимального значения, равного 32767.Таймер с задержкой выключения (TOF) используется для задержки выключения выхода на фиксированный интервал времени после выключения входа. Когда включается разрешающий вход, немедленно включается бит таймера, а текущее значение устанавливается в 0. Когда вход выключается, таймер ведет отсчет времени, пока истекшее время не достигнет предустановленного времени. Когда предустановленное время достигнуто, бит таймера сбрасывается, а отсчет текущего значения прекращается. Если выключен в течение более короткого интервала времени, чем предустановленное значение, то бит таймера остается включенным. Команда TOF должна обнаружить переход от включенного состояния к выключенному, чтобы начать отсчет времени. Если таймер TOF находится внутри области SCR, и область SCR не активна, то текущее значение устанавливается в 0, бит таймера выключается, и отсчет текущего значения не ведется.Команды циклического сдвигаКоманды Сдвинуть циклически байт вправо и Сдвинуть циклически байт влево циклически сдвигают содержимое входного байта (IN) вправо или влево на число разрядов, указанное в (N), и загружают результат в выходной байт (OUT). Циклический сдвиг является кольцевым. Если величина сдвига (N) больше или равна 8, то перед выполнением циклического сдвига от величины сдвига, указанной в (N), берется остаток от деления на 8. В результате величина сдвига находится в пределах от 0 до 7. Если величина сдвига равна нулю, то циклический сдвиг не производится. Если циклический сдвиг выполняется, то значение последнего циклически сдвинутого бита копируется в бит переполнения (SM1.1). Если величина сдвига не является целым кратным 8, то последний циклически выдвинутый бит копируется в бит переполнения (SM1.1). Бит нулевого значения (SM1.0) устанавливается, если подлежащая циклическому сдвигу величина равна нулю. Операции циклического сдвига байта вправо и влево являются беззнаковыми.
48 арифметические команды. Сложение и вычитание целых чисел.Команды Сложить целые числа и Вычесть целые числа складывают или вычитают два 16–битовых целых числа и дают 16–битовый результат (OUT).В LAD и FBD: IN1 + IN2 = OUT\IN1 – IN2 = OUT\В STL: IN1 + OUT = OUT\OUT – IN1 = OUT.Умножение и деление целых чисел.Команда Умножить целые числа перемножает два 16–битовых целых числа и дает 16–битовое произведение.Команда Разделить целые числа делит два 16–битовых целых числа и дает 16–битовое частное. Остаток не сохраняется.Бит переполнения устанавливается, если результат занимает долее одного слова.В LAD и FBD: IN1*N2 = OUT\IN1 / IN2 = OUT\В STL: IN1*OUT = OUT\OUT / IN1 =\OUTКоманды сравнения целых чисел.Команда Сравнить целые числа используется для сравнения двух величин: IN1 и IN2. Возможны следующие сравнения: IN1 = IN2, IN1>= IN2, IN1 <= IN2, IN1 > IN2, IN1 < IN2 и IN1 <> IN2.Целые числа сравниваются с учетом знака (16#7FFF > 16#8000).В LAD контакт включен, когда сравнение истинно.В FBD выход включен, когда сравнение истинно.В STL, если сравнение истинно, то эти команды загружают «1» в вершину стека или выполняют логическое сопряжение значения «1» со значением в вершине стека в соответствии с таблицей истинности для И или ИЛИ.
