23. Частные производные высших порядков функции многих переменных. Определение и символика. Привести примеры.

Частные производные и называют частными производными первого порядка. Их можно рассматривать как функции от (х; у) ϵ D. Эти функции могут иметь частные производные, которые называются частными производными второго порядка. Они определяются и обозначаются следующим образом:

Аналогично определяются частные производные З-го , 4-го и т. д. порядков. Так , .

Частная производная второго или более высокого порядка, взятая по различным переменным, называется смешенной частной производной. Таковыми являются, например, , , .

Пример: Найти частные производные второго порядка

функции . Решени Так и ,то , . => .

Теорема (Шварц). Если частные производные высшего порядка непрерывны, то смешанные производные одного порядка, отличающиеся лишь порядком дифференцирования , равны между собой . . В частности, для z = f(х; у) имеем :

24. Дифференциал функции многих переменных. Связь дифференциала и полного приращения функции многих переменных.

Пусть функция z = f ( x ; у) определена в некоторой окрестности точки М(х;у). Составим полное приращение функции в точке М: z = f ( x + х; у + у) - f ( x ; у).(*) Функция z = f ( x ; у) называется дифференцируемой в точке М(х; у), если ее полное приращение в этой точке можно представить в виде z = А· х + В· у + х +β у.(*), где = А, = В, = α( х, у)→ О и β= β ( х, у) → о при х → о, у → о. Сумма первых двух слагаемых в равенстве (*) представляет собой главную часть приращения функции. Главная часть приращение функции z = f ( x ; у), линейная относительно х и у, называется полным дифференциалом этой функции и обозначается символом dz: dz = А· х + В . у.

Равенство (*) можно переписать в виде , можно записать приближенное равенство . Приращения независимых переменных и 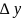-дифференциалы независимых переменных х и у, и обозначаются dx и dу. Тогда вырожение полного дифференциала : .

25. Восстановление вида функции по заданному полному дифференциалу.

Уравнение вида M(x,y)dx+N(x,y)dy=0 (1) называется уравнением полных дифференциалов, если выполняется равенство My=Nx.То что уравнение (1) является уравнением полных дифференциалов означает, что существует функцияF(x,y) такая, что выполняется следующее равенства:dF=Fxdx+Fydy=0 ;Fx=M(x,y); Fy=N(x,y)  (2). Метод восстановления функции:Чтобы найти функцию F нам нужно проинтегрировать 1-е или 2-е уравнение системы (2) F=∫Mdx+C(y) Затем полученное выражение продифференцируем по y и подставим в левую часть уравнения Fy=N(x,y): ∫Mydx+C′(y)=N(x,y) Откуда выразим C(y).Подставляя найденную функцию C(y) в (3) найдем функцию F. Решением исходного уравнения (1) будет кривая F(x,y)=C

26. Скалярное поле. Линии и поверхности уровня. Привести примеры.

Пусть в пространстве (х,у,z) имеется область D, в которой задана функция u=u(x,y,z). В этом случаи говорят, что в области D задано скалярное поле. Рассмотрим точки области D, в которых функция u(x,y,z) имеет постоянное значение с: u(x,y,z)=c. Совокупность этих точек образует некоторую поверхность. Если возьмем другое значение с, то получим другую поверхность. Эти поверхности называются поверхностями уровня. Если функция u есть функция двух переменных x и y u=u(x,y) то «поверхностями» уровня будут линии на плоскости Оху: u(x,y)=c, которые называются линиями уровня.

Пример1: пусть задано солярное поле . Поверхность уровня , то есть эллипсоиды с полуосями , , . Пример2: z=1-x^2-y^2. Линии уровня с=1-x^2-y^2, это окружности с радиусом (1-с)^(1/2)