21. Функция многих переменных. Определение. Область определения. Привести примеры.

все важнейшие факты теории функций нескольких переменных наблюдаются уже на функциях двух переменных.

Если каждой паре (х,у) значений двух, независимых друг от друга, переменных величин х и у, из некоторой области их изменения D соответствует определенное значение величины z, то мы говорим, что z есть функция двух независимых переменных х и у, определенная в области D. Записывается z = f ( x, у)

Совокупность пар (х,у) значений х и у, при которых определяется функция z=f(x,y), называется областью определения этой функции. Функцию z = f ( x ; у), где (х; у) ϵ D .можно понимать как функцию точки М(х; у) координатной плоскости Оху. В частности, областью определения может быть вся плоскость или ее часть, ограниченная некоторыми линиями . Линию, ограничивающую область, называют границей области. Точки области, не лежащие на границе, называются внутренними . Область, состоящая из одних внутренних точек, называется открытой. Область с присоединенной к ней границей называется замкнутой, обозначается D (с чертой сверху). Примером замкнутой области является круг с окружностью.

Пример1 площадь треугольника. S=xy/2 х-основание, у- высота. Область определения x>0, y>0(так как высота и основание не могут быть отрицательными.)

Пример2 z=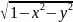 => 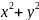≤1 . Все точки М(х,у) лежат к круге радиуса 1 с центром в начале координат и на границе этого круга.

22. Функция многих переменных. Определение. Предел и непрерывность функции многих переменных. Кривые и поверхности разрыва.

все важнейшие факты теории функций нескольких переменных наблюдаются уже на функциях двух переменных.

Если каждой паре (х,у) значений двух, независимых друг от друга, переменных величин х и у, из некоторой области их изменения D соответствует определенное значение величины z, то мы говорим, что z есть функция двух независимых переменных х и у, определенная в области D. Записывается z = f ( x, у)

Введем понятие окрестности точки. Множество всех точек М(х; у) плоскости, координаты которых удовлетворяют неравенству < б, называется б-окрестностью точки Мо(Хо; Уо). Другими словами, б-окрестность точки Мо - это все внутренние точки круга с центром Мо и радиусом б.

Предел: Пусть функция z = f ( x ; у) определена в некоторой окрестности точки Мо(Хо; Уо), кроме, быть может, самой этой точки. Число А называется пределом функции z = f ( x ; у) при х ≠ хо и у ≠ Уо если для любого ε > О существует б > О такое, что для всех х ≠хо и у ≠ уо и удовлетворяющих < б выполняется неравенство |f(x,y)-A|<ε. Записывают 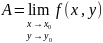или .

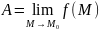Непрерывность функции многих переменных: Функция z = f ( x ; у) (или f (M)) называется непрерывной в точке Мо(хо; Уо), если она: .

а) определена в этой точке и некоторой ее окрестности, б) имеет предел в) этот предел равен значению функции z в точке , т. е.

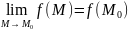
Функция, непрерывная в каждой точке некоторой области, называется непрерывной в этой области. Точки, в которых непрерывность нарушается (не выполняется хотя бы одно из условий непрерывности функции в точке), называются точками разрыва этой функции. Точки разрыва z = f ( x ; у) могут образовывать целые линии разрыва.

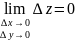Можно дать другое, равносильное приведенному выше, определение непрерывности функции z = f ( x ; у) в точке. Обозначим x = х-хо, y = у - Уо, z = f ( x ; у) - f(xo; Уо)· Величины x и y называются приращениями аргументов х и у, а z - ПОЛНЫМ приращением функции f ( x ; У) в точке Мо(хо; уо). Функция z = f ( x ; У) называется непрерывной в точке Мо(хо; Уо) ϵ D, если выполняется равенство полное приращение функции в этой точке стремится к улю, когда приращения ее аргументов х и У стремятся к нулю.