4. Расчетная часть

Проницаемость пород и ее распределение

Характер движения нефти или газа к забою добывающей скважины определяется двумя основными факторами:

• физико-химическими свойствами этих углеводородов;

• структурой порового пространства среды – коллектора, в которой они распространяются.

Для описания течения углеводородов с учетом этих факторов, наряду с другими характеристиками, вводится понятие проницаемости горной породы,

характеризующей ее способность пропускать жидкости и газы. Для оценки проницаемости пород обычно пользуются законом фильтрации Дарси, согласно которому скорость фильтрации (просачивания) жидкости в среде пропорциональна градиенту давления и обратно пропорциональна ее динамической вязкости :

.

Перепишем эту формулу в скалярной форме для одномерной задачи. Для этого выделим образец породы длиной , и предположим, что ее фильтрационные свойства одинаковы по всей длине. Тогда имеем

, (1.1)

где - скорость линейной (плоскопараллельной) фильтрации, - объемный расход жидкости в единицу времени, - площадь фильтрации, - перепад давления на выделенном участке пористой среды. Коэффициент пропорциональности в (1.1) называется коэффициентом проницаемости:

. (1.2)

Величина имеет размерность площади, и в системе СИ измеряется в :

.

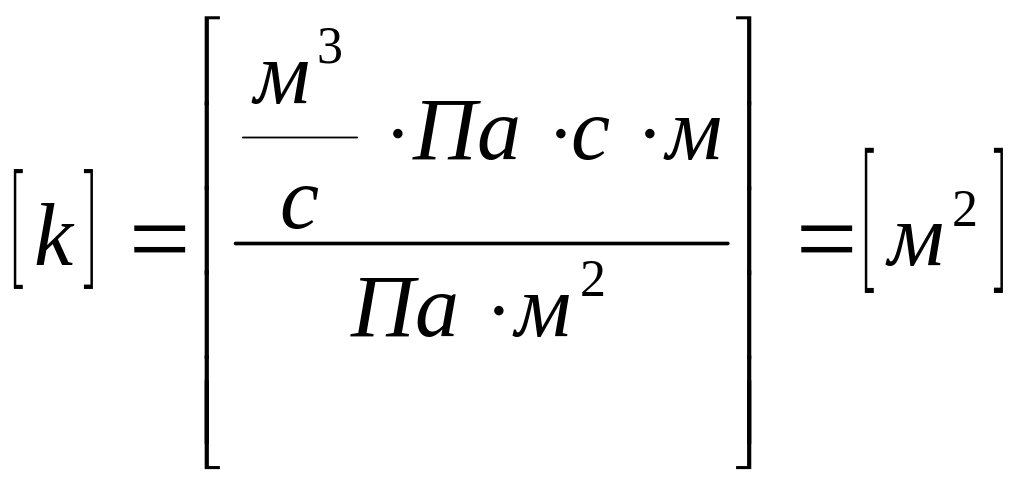i – номера интервалов, на которые разбивается весь наблюдаемый диапазон значений проницаемостей. Число таких интервалов в табл. 1 равно 10.

N_i – число пород, проницаемости которых лежат в i - том интервале. Общее число исследованных пород составляет .

p_i – относительное число пород, проницаемости которых попадают в i- тый интервал: , величина равна относительной доле образцов с выделенной проницаемостью. На языке математической статистики есть вероятность того, что проницаемость одной случайно выбранной породы из тысячи, попадет в интервал проницаемостей шириной .

Таблица 1

1i	Интервал проницаемостей (мкм2)	Ni	pi
11	0 – 0,2	4	0,004
22	0,2 – 0,4	126	0,126
33	0,4 – 0,6	230	0,230
44	0,6 – 0,8	260	0,260
55	0,8 – 1,0	130	0,130
66	1,0 – 1,2	120	0,120
77	1,2 – 1,4	50	0,050
88	1,4 – 1,6	30	0,030
99	1,6 – 1,8	30	0,030
110	1,8 - 2,0	20	0,020

Графическое представление данных и их характеристики

В качестве численных характеристик гистограмм чаще всего рассматривают два параметра – среднюю величину и дисперсию, и реже используют такие величины как наиболее вероятная и медиана. Определим два последних понятия. Наиболее вероятная величина распределения определяется как значение переменной, на которую приходится максимум распределения. Медианой называют такое значение переменной, относительно которой полная площадь под распределением делится на две равные части. В идеальном эксперименте, когда проводится большое число высокоточных измерений, средняя величина совпадает с т.н. математическим ожиданием. Средняя величина характеризует положение центра тяжести гистограммы на оси абсцисс, а дисперсия - ширину распределения вдоль нее. Вычислим эти характеристики по данным табл. 1. По определению, средняя величина проницаемости есть

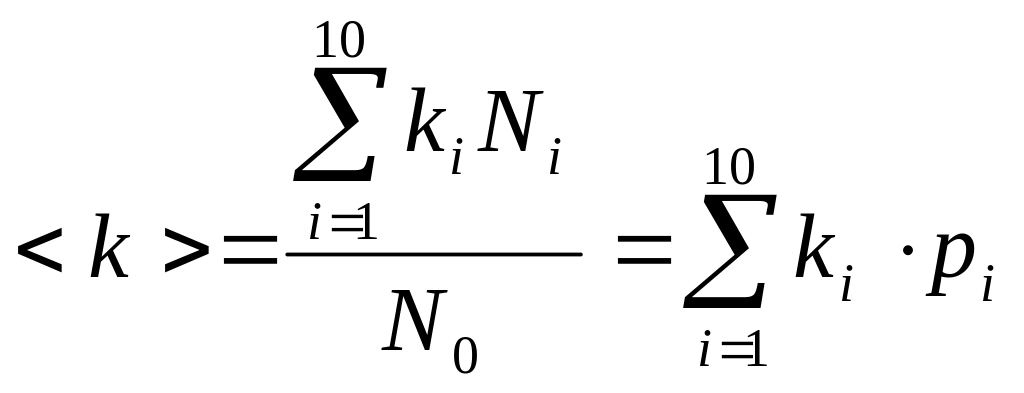, (2.1)

где

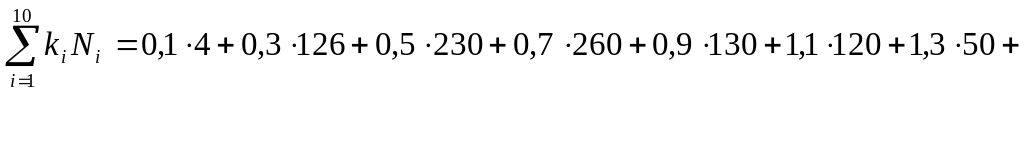
(2.2)

Формула (2.1) применяется для вычисления средней величины в случае, когда исходные данные предварительно распределены по отдельным ячейкам, т.е. в виде табл. 1. В этом случае мы не располагаем данными по отдельно взятым породам. В случае, когда известны проницаемости каждой из тысячи рассмотренных пород, средняя проницаемость вычисляется как средняя арифметическая

.

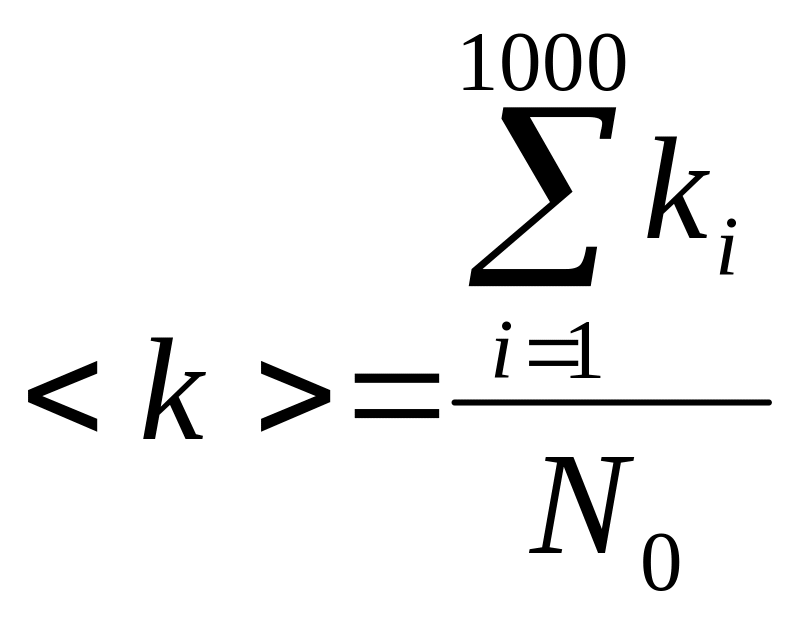Таким образом, мы вычислили среднюю проницаемость горных пород, хотя и для достаточно большой, но ограниченной выборки пород . Поэтому, полученная величина является приближенной. Поясним сказанное. Предположим, что у нас имеется возможность выбора образцов горных пород из неограниченно большого набора пород. Результат (2.2) получен для одной выборки, состоящей из 1000 образцов. Если проделать аналогичную процедуру для другой выборки из 1000 образцов, то получаемый результат может оказаться близким, но не совпадающим с (2.2). Увеличивая, таким образом, число исследуемых образцов в одной выборке можно повысить точность определения величины средней проницаемости. При бесконечно большом числе исследуемых образцов эта величина неограниченно приближается к истинной средней величине , т.е. к математическому ожиданию. Поскольку величина часто используется в уравнениях гидродинамики в качестве основного параметра фильтрации жидкости, то здесь следует оговорить одну возможную особенность ее использования. В общем случае, средняя проницаемость пород, определяемая для большой совокупности образцов пород, может оказаться малоинформативной характеристикой грунта. Например, в случае, если в выбранную совокупность пород ввести тонкую перегородку со сравнительно низкой проницаемостью, то величина , рассчитанная по формуле (2.2), может измениться несущественно, тогда, как скорость фильтрации будет определяться, в основном, проницаемостью этой тонкой перегородки. В аналогичных случаях бывает полезным использование метода сопряженных уравнений, содержащих наряду со средними величинами и моменты более высоких порядков, каковой является, например, дисперсия распределения. Эта величина характеризует степень «рассеяния» совокупности результатов опытов относительно средней величины. Конкретное рассмотрение дисперсии проделаем на основе результатов табл. 1. Вычислим дисперсию распределения проницаемостей. По определению

, (2.3)

где - математическое ожидание.

В формуле (2.3) математическое ожидание не известно, и поэтому вычислим приближенное значение дисперсии с использованием средней проницаемости (2.2), определенной из опыта.

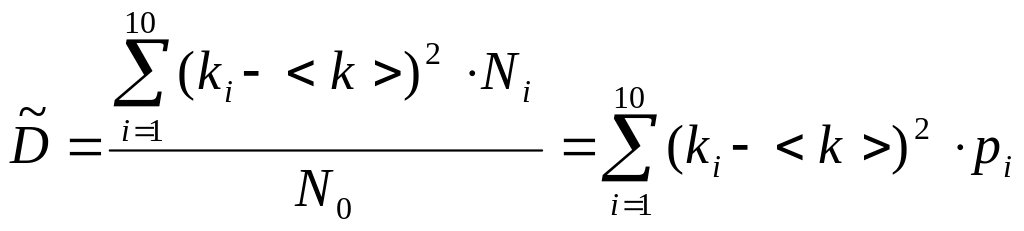. (2.4)

Применим эту формулу к данным табл. 1.

.

. (2.5)

Здесь отметим, что формулы (2.3) и (2.4), вообще говоря, являются приближенными. Они справедливы только в случае больших значений . Для сравнительно малых значений нужно пользоваться более точной формулой:

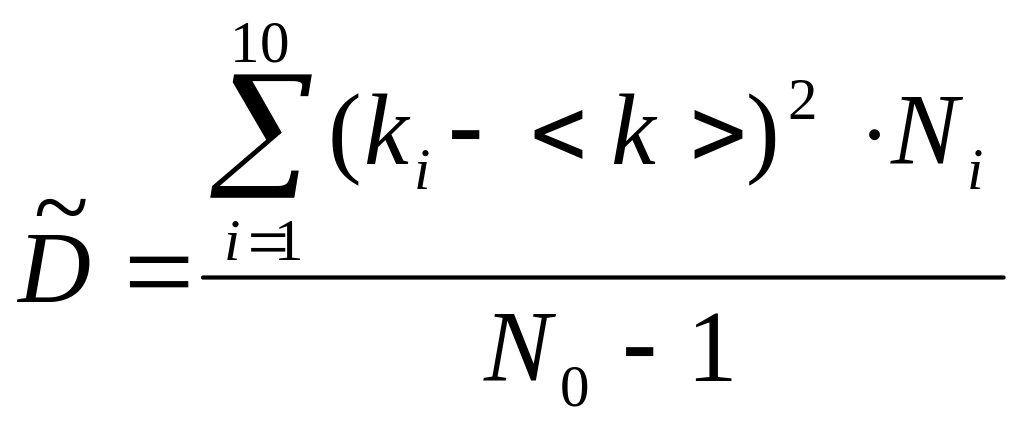. (2.6)

Отличие знаменателей правых частей формул (2.6) и (2.4) обусловлено тем, что сумма в числителе должна быть отнесена не к числу образцов , а к числу подлинно независимых значений . Здесь можно предположить, что все 1000 измерений в табл. 1 являются независимыми. Но в формуле (2.6) выражается через среднюю проницаемость , которая вычислена по формуле (1) с использованием тех же данных. Этим мы накладываем одно условие связи на имеющуюся совокупность данных, после чего независимых становится . В этом смысле величину в (2.6) называют числом степеней свободы. Поскольку величина , в рассматриваемом нами случае, достаточно велика, то дисперсия, вычисленная по формуле (2.6) совпадает с (2.5).

Как уже отмечалось, дисперсия является одной из важнейших характеристик статистического распределения, и характеризует ее ширину. Она обладает следующими важными свойствами (без доказательства).

1. Дисперсия постоянной величины равна нулю: .

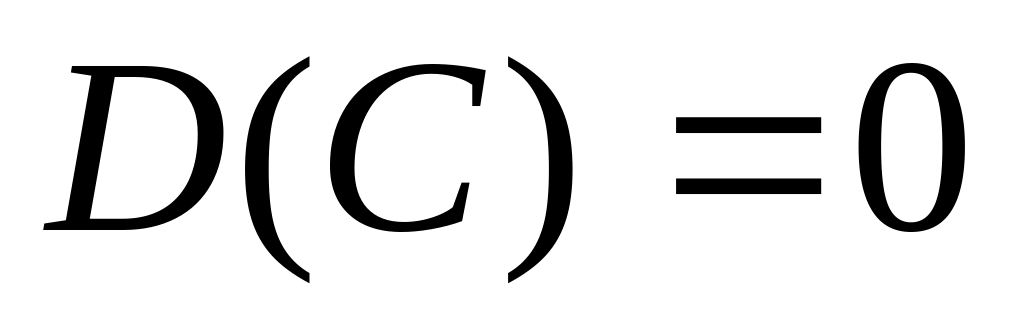2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат: .

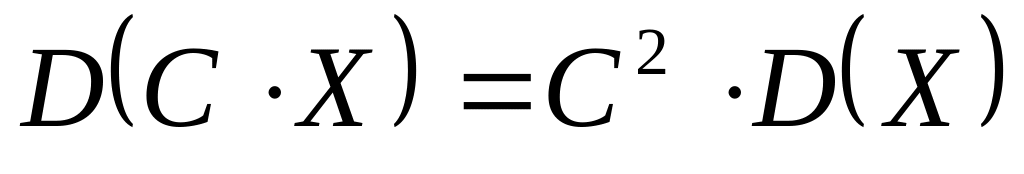3. Дисперсия суммы нескольких взаимно независимых случайных величин равна сумме дисперсий этих величин: .

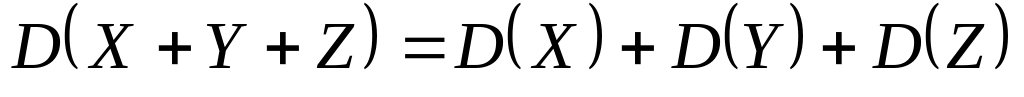Вычисление погрешности средней проницаемости

Величины средней проницаемости и ее дисперсии, вычисленные в предыдущем пункте по формулам (2.1) и (2.6), являются приближенными, т.к. они получены по ограниченному числу измерений. В этом разделе рассмотрим способ вычисления величины погрешности, с которой определена средняя проницаемость (2.2). Поскольку дисперсия характеризует ширину распределения, или более конкретно, степень отклонения имеющейся совокупности данных от средней величины, то она является мерой абсолютной погрешности в определении средней проницаемости (величину часто называют просто погрешностью). Но отождествление абсолютной величины экспериментальной дисперсии с погрешностью не имеет явного смысла, т.к. они имеют разные размерности (см. формулы (2.2) и (2.5). Поэтому для наглядной характеристики рассеивания опытных данных следует пользоваться величиной, размерность которой совпадает с размерностью . Такой величиной является квадратный корень из дисперсии :

(3.1)

В соответствующей литературе эту величину называют по-разному - среднеквадратичным отклонением, среднеквадратичной погрешностью или стандартом. Стандарт характеризует вероятность попадания величины проницаемости одной случайно выбранной породы в интервал . Величина называется относительной погрешностью или относительной дисперсией. Но это только частный случай. В общем случае величина не совпадает с абсолютной погрешностью . В частности, такое утверждение следует из того, что стандарт , также, как и , не зависит явно от числа образцов . Это означает, что погрешность также не зависит от . Такое утверждение противоречит простой логике, т. к. с ростом числа образцов , степень точности с которой вычисляется средняя проницаемость должна расти. Следовательно, погрешность должна уменьшаться с ростом . Получим эту зависимость. В табл. 1 приведены результаты сеансов независимых измерений. Средняя проницаемость вычисляется по формуле (2.1):

.

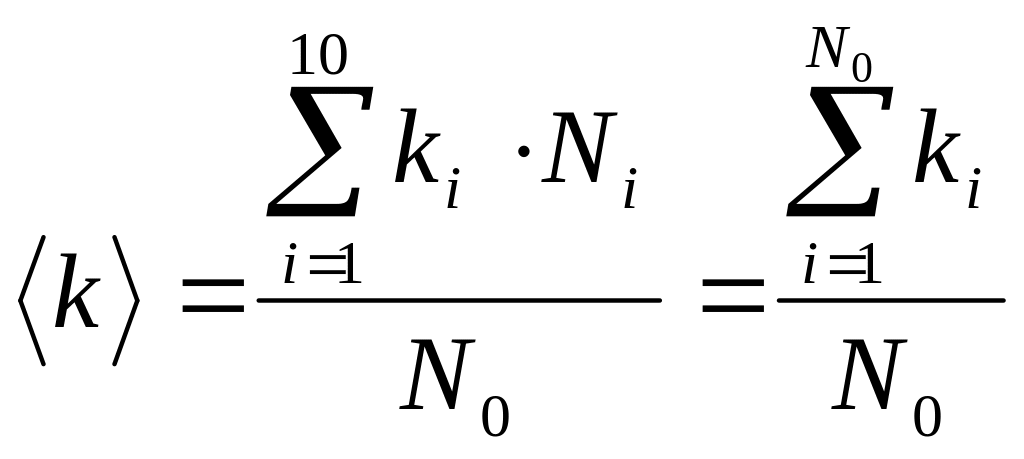Вычислим теперь дисперсию средних величин . Используя свойства дисперсий, приведенные в конце предыдущего пункта получаем

.

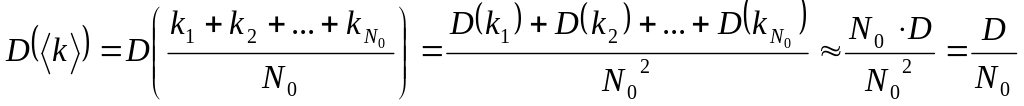Следовательно, величина относительной погрешности распределения средних проницаемостей равна

,

т. е., относительная погрешность распределения средних проницаемостей, в раз меньше относительной погрешности одного отдельного измерения. Следовательно, с ростом числа испытуемых пород погрешность уменьшается, и для данных, приведенных в табл. 1, получаем

. (3.2)

Величину абсолютной погрешности , определенную таким образом, часто называют, наряду с (3.1), также среднеквадратичным отклонением. Таким образом, средняя величина проницаемости, определенная по данным табл. 1, равна

, (3.3)

т.е. она определена с относительной погрешностью

. (3.4)

Изложенный способ вычисления погрешности средней проницаемости используется часто, но следует отметить, что он является приближенным и имеет оценочный характер. При более строгом рассмотрении вопроса вычисления погрешности вводится понятие доверительного интервала и доверительной вероятности, которая характеризует точность и надежность оценки . По данным табл. 1 мы нашли, что . Зададим некоторую большую вероятность . Пусть истинная средняя проницаемость пород отличается от вычисленной величины на величину с вероятностью

. (3.5)

Это равенство означает, что с вероятностью неизвестное значение средней проницаемости попадает в интервал

. (3.6)

Вероятность называется доверительной вероятностью, а интервал - доверительным интервалом.

Рассмотрим теперь общий случай. До сих пор мы рассматривали величину , полученную по данным одной серии измерений проницаемостей для 1000 образцов пород. Предположим далее, что мы располагаем результатами большого числа таких измерений, каждая из которых характеризуется средней величиной , вычисленной по формуле (2.1). Тогда, согласно центральной предельной теореме теории вероятностей, распределение по числу полученных средних будет описываться нормальным распределением

, (3.7)

где . Эта функция представляет собой нормальную функцию распределения с параметрами и , и характеризует вероятность того, что случайно выбранная величина имеет значение, меньшее чем (см. Приложение). Здесь отметим, что

, (3.8)

т.е. полная площадь под функцией плотности вероятностей нормального распределения равна единице, или, применяя стандартную терминологию, следует сказать, что эта функция нормирована. Поскольку, в рассматриваемом нами примере, проницаемость является положительной величиной, то величины и могут принимать произвольные положительные значения. В этом случае нормальная функция распределения имеет вид

. (3.9)

Из (3.8) и (3.9) следует, что измеренная в одной серии опытов средняя проницаемость имеет величину, большую, чем некоторая критическая величина с вероятностью . Эта вероятность соответствует затененной части площади под функцией плотности вероятностей. Тогда в силу симметрии рассматриваемой функции, величина попадает в интервал с вероятностью

. (3.10)

Перепишем (3.10) используя (3.5) и (3.9)

. (3.11)

Приравнивая правые части (2.11) и (3.11) получаем уравнение для границ доверительного интервала

,

откуда

, (3.12)

где - функция, обратная .

Как уже отмечалось, истинное значение нам не известно, и поэтому в (3.12) подставляют ее приближенное значение , определяемое из опыта. Вычисляя, таким образом, величину , можно определить доверительный интервал (3.5). При вычислении , как правило, используют табличные данные функции в зависимости от . Величина , приведенная в табл. 2, определяет для нормального закона число среднеквадратических отклонений, которое нужно отложить справа и слева от средней величины, чтобы вероятность попадания в полученный участок была равна :

, (3.13)

где вычисляется по формуле (3.2).

Используя результаты, приведенные в табл. 2 можно сказать, что средняя проницаемость горных пород, определяемая по данным табл. 1, с доверительной вероятностью попадает в интервал с доверительными границами :

,

.

Из табл. 2 следует, что чем больше доверительная вероятность , тем больше величина , и тем сильнее отличаются границы доверительного интервала.

Таблица 2

0,8	1,282	0,86	1,475	0,91	1,694	0,97	2,169
0,81	1,310	0,87	1,513	0,92	1,750	0,98	2,325
0,82	1,340	0,88	1,554	0,93	1,810	0,99	2,576
0,83	1,371	0,89	1,597	0,94	1,880	0,997	3,000
0,84	1,404	0,90	1,643	0,95	1,960	0,999	3,290
0,85	1,439			0,96	2,053

Таким образом, мы рассмотрели приближенный метод построения доверительного интервала, не зная при этом истинного закона распределения проницаемостей пород. В том случае, когда этот закон известен, задача построения доверительного интервала решается точно, т.к. при вычислении дисперсии, мы вместо (2.6) можем пользоваться точной формулой

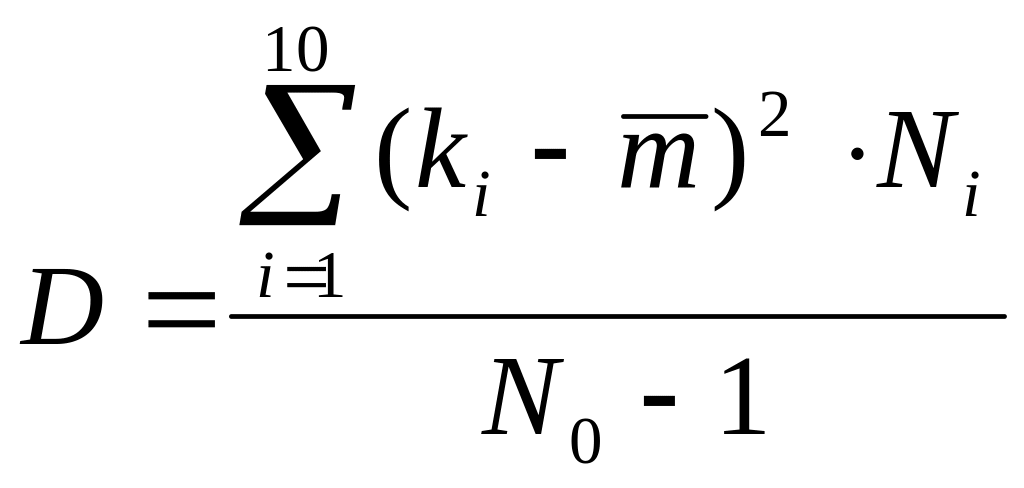, (3.14)

где есть математическое ожидание, вычисляемое как первый момент распределения :

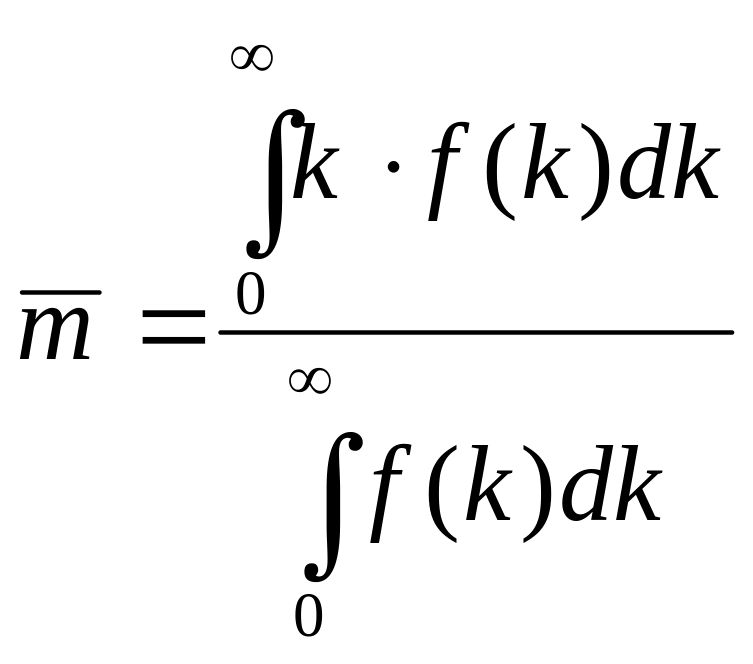. (3.15)

Например, если бы распределение проницаемостей горных пород описывалось нормальным распределением, то задача построения точного доверительного интервала для средней проницаемости свелась бы к соответствующему анализу распределения Стьюдента.