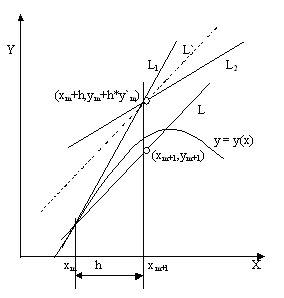
Тангенс угла наклона прямой l и прямой l равен

Ф(x_my_mh)=½[f(x_my_m)+f(x_m+hy_m+y_mh)] 1.2.

где y_m=f(x_my_m) 1.3.

Уравнение линии L при этом записывается в виде

y=y_m+(x-x_m)Ф(x_my_mh)

так что

y_m+1=y_m+hФ(x_my_mh) 1.4.

Соотношения 121314 описывают исправленный метод Эйлера

Чтобы выяснитьнасколько хорошо этот метод согласуется с разложением в ряд Тейлоравспомнимчто разложение в ряд функции f(xy) можно записать следующим образом:

f(xy)=f(x_my_m)+(x-x_m)f/x+(y-y_m)f/x+1.5.

где частные производные вычисляются при x=x_mи y=y_m

Подставляя в формулу 15 x=x_m+h и y=y_m+hy_m и используя выражение 13 для y_m получаем

f(x_m+hy_m+hy_m)=f+hf_x+hff_y+O(h²)

где снова функция f и ее производные вычисляются в точке x_my_mПодставляя результат в 12 и производя необходимые преобразованияполучаем

Ф(x_my_mh)=f+h/2(f_x+ff_y)+O(h²)

Подставим полученное выражение в 14 и сравним с рядом Тейлора

y_m+1=y_m+hf+h²/2(f_x+ff_y)+O(h³)

Как видимисправленный метод Эйлера согласуется с разложением в ряд Тейлора вплоть до членов степени h²являясьтаким образомметодом Рунге-Кутты второго порядка

Рассмотрим модификационный метод ЭйлераРассмотрим рис3 где первоначальное построение сделано так жекак и на рис2Но на этот раз мы берем точкулежащую на пересечении этой прямой и ординатой x=x+h/2На рисунке эта точка образована через Ра ее ордината равна y=y_m+(h/2)y_mВычислим тангенс угла наклона касательной в этой точке

Ф(x_my_mh)=f+(x_m+h/2y_m+h/2*y_m)1.6.

где y_m=f(x_my_m) 1.7.

Прямая с таким наклономпроходящая через Робозначена черезL^*Вслед за теммы проводим через точку xmym прямую параллельнуюL^*и обозначаем ее через L₀Пересечение этой прямой с ординатой x=x_m+h и даст искомую точку x_m+1y_m+1Уравнение прямой можно записать в виде y=y_m+(x-x_m)Ф(x_my_mh)

где Ф задается формулой 16Поэтому

y_m+1=y_m+hФ(x_my_mh)1.8.

Соотношения 161718 описывают так называемый модификационный метод Эйлера и является еще одним методом Рунге-Кутта второго порядкаОбобщим оба методаЗаметимчто оба метода описываются формулами вида

y_m+1=y_m+hФ(x_my_mh) 1.9.

и в обоих случаях Ф имеет вид

Ф(x_my_mh)=a₁f(x_my_m)+a₂f(x_m+b₁hy_m+b₂hy_m) 1.10.

где y_m=f(x_my_m) 111.

В частностидля исправленного метода Эйлера

a₁=a₂=1/2;

b₁=b₂=1

В то время как для модификационного метода Эйлера

a₁=0a₂=1

b₁=b₂=1/2

Формулы 19110111 описывают некоторый метод типа Рунге-КуттыПосмотримкакого порядка метод можно рассчитывать получить в лучшем случае и каковы допустимые значения параметров a₁a₂b₁и b₂

Чтобы получить соответствие ряду Тейлора вплоть до членов степени hв общем случае достаточно одного параметраЧтобы получить согласование вплоть до членов степени h²потребуется еще два параметратак как необходимо учитывать члены h²f_xи h²ff_yТак как у нас имеется всего четыре параметратри из которых потребуются для создания согласования с рядом Тейлора вплоть до членов порядка h²то самое лучшеена что здесь можно рассчитывать - это метод второго порядка

В разложении f(xy) в ряд 15 в окрестности точки x_my_mположим x=x_m+b₁h

y=y_m+b₂hf

Тогда f(x_m+b₁hy_m+b₂hf)=f+b₁hf_x+b₂hff_y+O(h²)где функция и производные в правой части равенства вычислены в точке x_my_m

Тогда 19 можно переписать в виде y_m+1=y_m+h[a₁f+a₂f+h(a₂b₁f_x+a₂b₂ff_y)]+O(h³)

Сравнив эту формулу с разложением в ряд Тейлораможно переписать в виде

y_m+1=y_m+h[a₁f+a₂f+h(a₂b₁f_x+a₂b₂ff_y)]+O(h³)

Если потребовать совпадения членов hfто a₁+a₂=1

Сравнивая членысодержащие h²f_xполучаем a₂b₁=1/2

Сравнивая членысодержащие h²ff_yполучаем a₂b₂=1/2

Так как мы пришли к трем уравнениям для определения четырех неизвестныхто одно из этих неизвестных можно задать произвольноисключаяможет бытьнульв зависимости от тогокакой параметр взять в качестве произвольного

Положимнапримерa₂=0тогда a₁=1-b₁=b₂=1/2и соотношения 19110111 сведутся к

y_m+1=y_m+h[(1-)f(x_my_m)+f(x_m+h/2y_m+h/2f(x_my_m))]+O(h³) 1.12

Это наиболее общая форма записи метода Рунге-Кутта второго порядкаПри=1/2 мы получаем исправленный метод Эйлерапри=1 получаем модификационный метод ЭйлераДля всехотличных от нуляошибка ограничения равна

e_t=kh³1.13.

Методы Рунге-Кутта третьего и четвертого порядков можно вывести совершенно аналогично томукак это делалось при выводе методов первого и второго порядковМы не будем воспроизводить выкладкиа ограничимся темчто приведем формулыописывающие метод четвертого порядкаодин из самых употребляемых методов интегрирования дифференциальных уравненийЭтот классический метод Рунге-Кутта описывается системой следующих пяти соотношений

y_m+1=y_m+h/6(R₁+2R₂+2R₃+R₄) 1.14.

где R₁=f(x_my_m)1.15.

R₂=f(x_m+h/2y_m+hR₁/2)1.16.

R₃=f(x_m+h/2y_m+hR₂/2)1.17.

R₄=f(x_m+h/2y_m+hR₃/2). 1.18.

Ошибка ограничения для этого метода равна e_t=kh⁵

так что формулы 114.-118. описывают метод четвертого порядка Заметим что при использовании этого метода функцию необходимо вычислять четыре раза