Лабораторная работа - Задача Коши

Тема: Задача Коші.

Мета роботи: Засвоїти методи розв'язання диференціальних рівнянь першого роду.

Завдання:

1. Методами Рунге-Кутта четвертого порядку та Адамса четвертого порядку розв'язати диференціальне рівняння.

на відрізку [x0;x0+1].

Аналітичний розв”язок задачі:

Резутьтати роботи

Файл out.txt

Runge-Kutta:

0 -2

0.1 -2.0301 Real: 0.010202 2.0403

0.2 -2.12162 Real: 0.0433315 2.16495

0.3 -2.27835 Real: 0.10775 2.3861

0.4 -2.50702 Real: 0.22034 2.72736

0.5 -2.81805 Real: 0.41218 3.23023

0.6 -3.22666 Real: 0.739596 3.96626

0.7 -3.75463 Real: 1.30558 5.06022

0.8 -4.43296 Real: 2.30185 6.73481

0.9 -5.30581 Real: 4.093 9.39881

1 -6.43654 Real: 7.38906 13.8256

Max error R-K: 13.8256

Adamsa-Bashfort:

0.4 -2.50684 Real: 0.22034 2.72718

0.5 -2.81753 Real: 0.41218 3.22971

0.6 -3.22557 Real: 0.739596 3.96517

0.7 -3.75263 Real: 1.30558 5.05821

0.8 -4.42947 Real: 2.30185 6.73132

0.9 -5.2999 Real: 4.093 9.3929

1 -6.42669 Real: 7.38906 13.8157

Max error A-B: 13.8256

Побудуємо графіки залежностей:

1. Побудуємо графіки самої функції, значень функції обчислених за допомогою методів Рунге-Кутта та Адамса четвертого порядку.

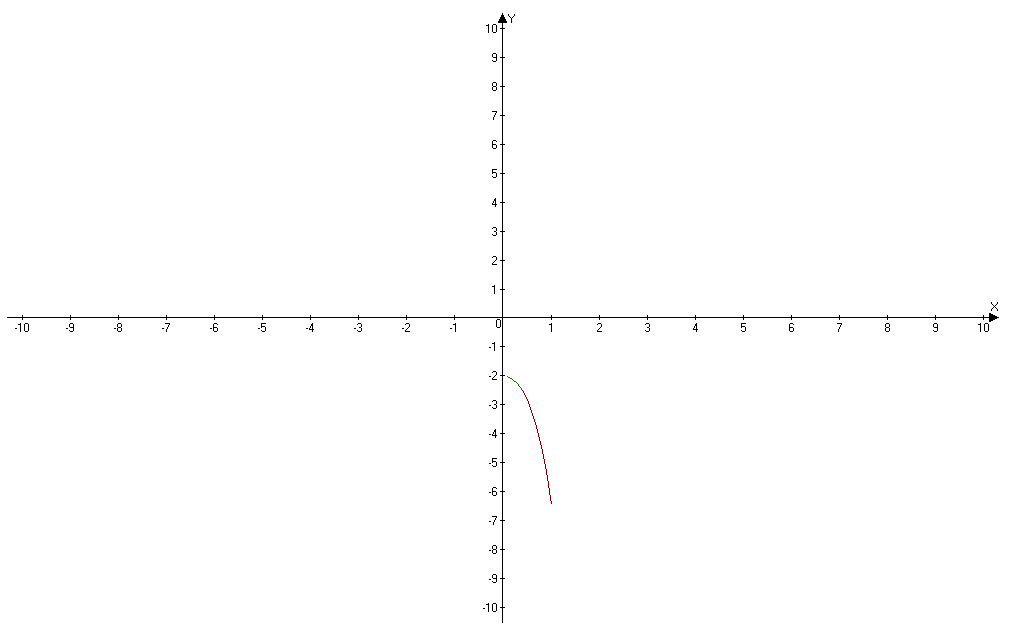
Так,як похибка в цьому випадку мінімальна, то ці графіки майже накладаються.

2. Графіки помилок:

1)Нижній – метод Адамса.

метод Рунге-Кутта

метод Адамса

3) Побудуйте графіки залежності e(h) для обох методів.

а) - метод Рунге-Кутта.

б)

- Метод Адамса.

Аналіз результатів.

1)Обидва графіки(3а,3б) нагадують параболи 4 порядку(різке зростання вверх).

Це підтверджує теоретичні обгрунтування.

2) метод Рунге-Кутта працює за довільних h значно точніше методу Адамса.

Це показано на графіках(2а,2б)

Текст програми:

#include <iostream.h>

#include <fstream.h>

#include <conio.h>

#include <math.h>

double f(double,double);

double realfun(double);

void main()

{

double x[50],y[50],F1,F2,F3,F4,max,er;

int i,j,n;

x[0]=0;

y[0]=-2;

n=10;

double h=1.0/n;

ofstream fout("out.txt");

max=0;

clrscr();

fout<<"Runge-Kutta:"<<endl;

fout<<x[0]<<"\t"<<y[0]<<endl;

for(i=0;i<n;i++){

x[i+1]=x[i]+h;

F1=f(x[i],y[i]);

F2=f(x[i]+h/2.0,y[i]+h/2.0*F1);

F3=f(x[i]+h/2.0,y[i]+h/2.0*F2);

F4=f(x[i+1],y[i]+h*F3);

y[i+1]=y[i]+(F1+2*F2+2*F3+F4)*h/6.0;

er=fabs(realfun(x[i+1])-y[i+1]);

if (er>max) max=er;

fout<<x[i+1]<<" \t"<<y[i+1]<<" \t Real: "<<realfun(x[i+1])<<" \t "<<er<<endl;

}

fout<<"Max error R-K: "<<max<<endl;

fout<<"Adamsa-Bashfort:"<<endl;

for(i=3;i<n;i++){

y[i+1]=y[i]+(h/24.0)*(55*f(x[i],y[i])-59*f(x[i-1],y[i-1])+37*f(x[i-2],y[i-2])-9*f(x[i-3],y[i-3]));

er=fabs(realfun(x[i+1])-y[i+1]);

if (er>max) max=er;

fout<<x[i+1]<<" \t"<<y[i+1]<<" \t Real: "<<realfun(x[i+1])<<" \t "<<er<<endl;

}

fout<<"Max error A-B: "<<max<<endl;

}

double f(double x,double y){

return 2*((x*x*x)-x+y*x);

}

double realfun(double x){

return (x*x)*exp(2*(x*x));

}