Министерство образования и науки Российской Федерации

Федеральное агентство по образованию

Государственное образовательное учреждение

высшего профессионального образования

«Уфимский государственный нефтяной технический университет»

Кафедра «Вычислительная техника и инженерная кибернетика»

«Решение системы нелинейных уравнений»

ОТЧЁТ

по лабораторной работе № 9

(Вариант № 45)

Выполнил ст. гр. ПО-01-01 _____________ Исхаков И.И.

(подпись, дата)

Проверил доцент каф. ВТИК _____________ Мухамадеев И. Г.

(подпись, дата)

Уфа, 2003

1. Постановка задачи.

Дана подынтегральная функция и её первообразная .

Требуется вычислить приближенное значение с точностью  = 0.001, 0.0001, используя формулы численного интегрирования (квадратурную формулу). Полученное значение сравнить с точным значением интеграла I_т, рассчитанным по формуле Ньютона-Лейбница.

2. Анализ задачи.

Необходимо создать программу вычисления приближенного значения интеграла по формуле трапеций и Ньютона-Котеса 5 порядка, с помощью созданной программы вычислить приближенное значение интеграла с требуемой точностью, используя алгоритм автоматического выбора шага интегрирования для метода трапеций.

Расчетная формула для одного Ньютона-Котеса участка выглядит следующим образом:

где –– коэффициенты Ньютона - Котеса, а k — число использующихся ординат на участке

Для проверки правильности вычислим тот же интеграл по формуле Ньютона-Лейбница:

a=1

b=2.2

I=F(b)-F(a);

I=()-()=()-()=

=-1.5-(-1,19155)= 0,30845

Так же для проверки правильности выполним вычисление в MathCAD

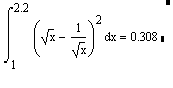
4. Текст программы

//------------------------------------------------------------------------

#include <vcl.h>

#pragma hdrstop

#include "math.h"

#include "Unit1.h"

//------------------------------------------------------------------------

#pragma package(smart_init)

#pragma resource "*.dfm"

TForm1 *Form1;

//------------------------------------------------------------------------

__fastcall TForm1::TForm1(TComponent* Owner)

: TForm(Owner)

{

}

//------------------------------------------------------------------------

float func(float x){

return (sqrt(x)-1.0/sqrt(x))* (sqrt(x)-1.0/sqrt(x));}

float Func(float x){

return (x*x)/2-2*x+log(fabs(x));}

void __fastcall TForm1::Button1Click(TObject *Sender)

{

float a=StrToFloat(Edit1->Text);

float b=StrToFloat(Edit2->Text);

float E=StrToFloat(Edit3->Text);

float S=0,S0,Sigma;

int n=1;

do{ n=2*n;

S0=S;

float h=(b-a)/n;

S=(func(a)+func(b))/2;

for (int i=1;i<n;i++)

S=S+func(a+i*h);

S=h*S;

Sigma=S-S0;

}while(fabs(Sigma)>=E);

Edit4->Text=FloatToStr(S);

Edit5->Text=FloatToStr(Sigma);

Edit6->Text=FloatToStr(n);

Edit7->Text=FloatToStr(fabs(S-(Func(b)-Func(a))));

}

//-----------------------------------------------------------------------

void __fastcall TForm1::Button2Click(TObject *Sender)

{

float a=StrToFloat(Edit1->Text);

float b=StrToFloat(Edit2->Text);

float H[6],x[6],W[6],k,I=0;

H[0]=H[5]=19.0/288.0; H[1]=H[4]=25.0/96.0;H[2]=H[3]=25.0/144.0;

k=5 ;

for(int i=0;i<=k;i++){

x[i]=a+i*(b-a)/k;

W[i]=(b-a)*H[i];

I=I+W[i]*func(x[i]);

}

Edit4->Text=FloatToStr(I);

Edit7->Text=FloatToStr(fabs(I-(Func(b)-Func(a))));

}

//------------------------------------------------------------------------

5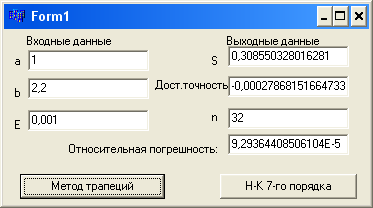 . Результаты расчётов, выполненные с помощью подготовленной программы на Си. Анализ и проверка

Метод трапеции  = 0.001

М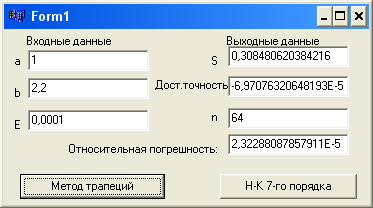 етод трапеции  = 0.0001

M етод Ньютона-Котеса 5

Результаты, полученные двумя методами по разработанной программе, совпали с требуемой точностью с результатами, полученными вручную в MathCADе, следовательно, задача решена верно