Министерство образования и науки Российской Федерации

Федеральное агентство по образованию

Государственное образовательное учреждение

высшего профессионального образования

«Уфимский государственный нефтяной технический университет»

Кафедра «Вычислительная техника и инженерная кибернетика»

ОТЧЁТ

по лабораторной работе № 8

«Решение системы нелинейных уравнений»

(Вариант № 100)

Выполнил студент гр. ПО-04-01 _____________ А.А. Бусов

(подпись, дата)

Проверил доцент каф. ВТИК _____________ И.Г. Мухамадеев

(подпись, дата)

Уфа, 2006

1. Постановка задачи.

Дана система нелинейных уравнений F(X) = 0.

Требуется найти решения системы методом простых итераций с улучшением Зейделя с точностью  = 0.001, 0.0001.

2. Анализ задачи.

Запишем систему в стандартном виде

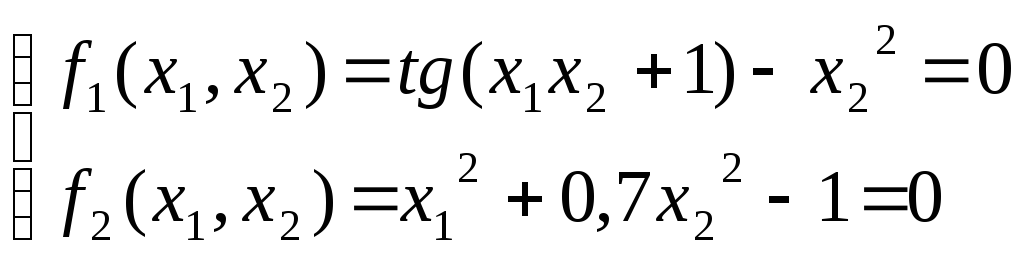
Область определения функций системы:

D_f1 = {-∞ < x₁ < ∞; -∞ < x₂ < ∞};

D_f2 = {-1 ≤ x₁ ≤ 1; -1,195 ≤ x₂ ≤ 1,195};

Область существования решений системы:

D_o = {-1 ≤ x₁ ≤ 1; -1,195 ≤ x₂ ≤ 1,195};

В MathCADе построим графики функций:

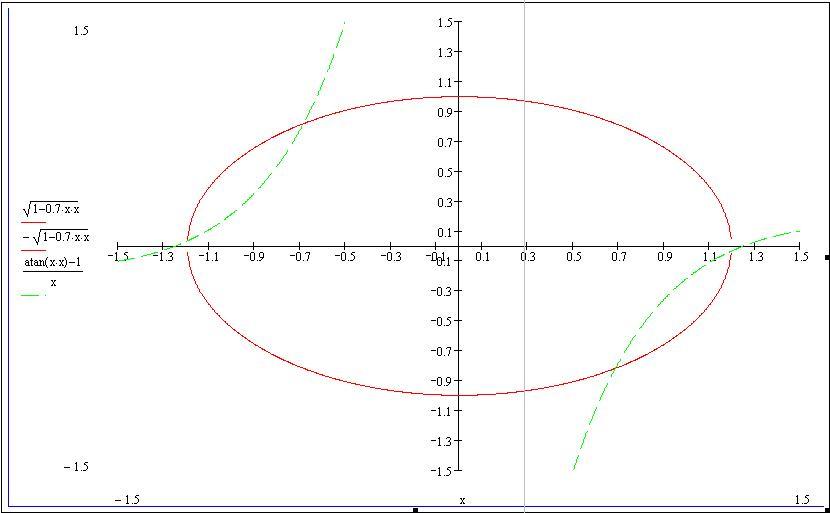
По графику видно, что данная система имеет 4 решения:

D_I = {0 < x₁ < 0,1; -1,3 < x₂ < -1,1};

D_II = {0,7 < x₁ < 0,9; -0,6 < x₂ < -0,8};

D_III = {-0,1 < x₁ < 0; 1,1 < x₂ < 1,3};

D_VI = {-0,9 < x₁ < -0,7; 0,6 < x₂ < 0,8};

Получим формулы сходящегося итерационного процесса для всех решений системы.

Для решения I:

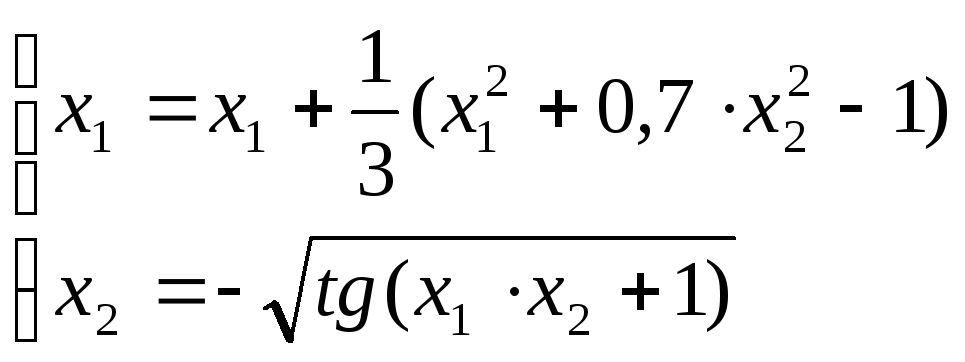
Определим частные производные:

Проверим условия сходимости в окрестности первого решения, взяв точку из области существования этого решения х₁=0,1; х₂=-1,2.

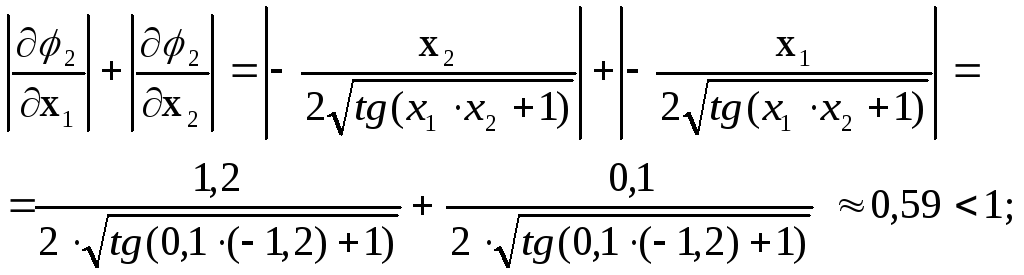
Условия сходимости соблюдаются, следовательно полученную эквивалентную систему можно использовать для уточнения первого решения.

Для решения II:

Определим частные производные:

Проверим условия сходимости в окрестности второго решения, взяв точку из области существования этого решения х1=0,7; х2=-0,7.

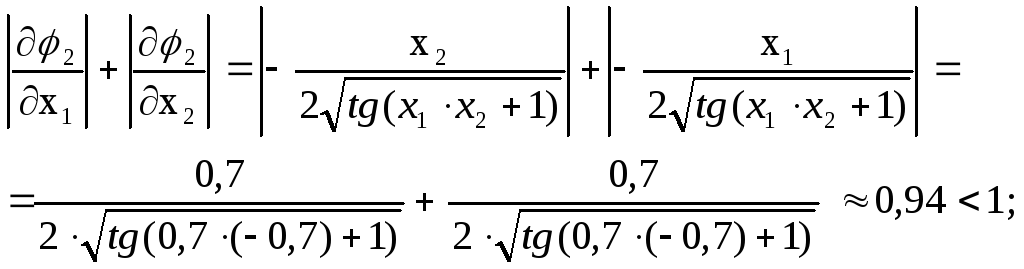
Условия сходимости соблюдаются, следовательно полученную эквивалентную систему можно использовать для уточнения второго решения.

Для решения III:

Определим частные производные:

Проверим условия сходимости в окрестности первого решения, взяв точку из области существования этого решения х₁=-0,1; х₂=1,2.

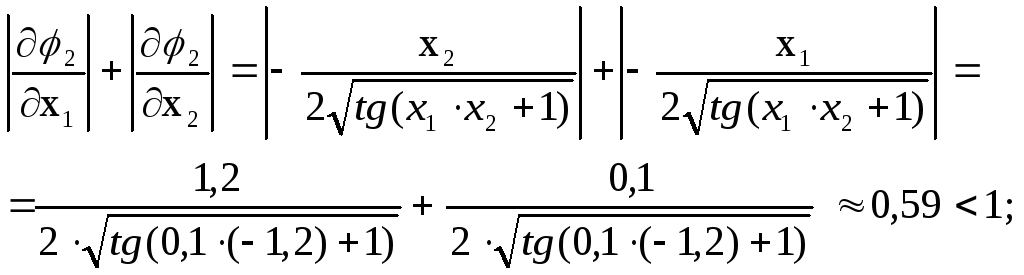
Условия сходимости соблюдаются, следовательно полученную эквивалентную систему можно использовать для уточнения третьего решения.

Для решения VI:

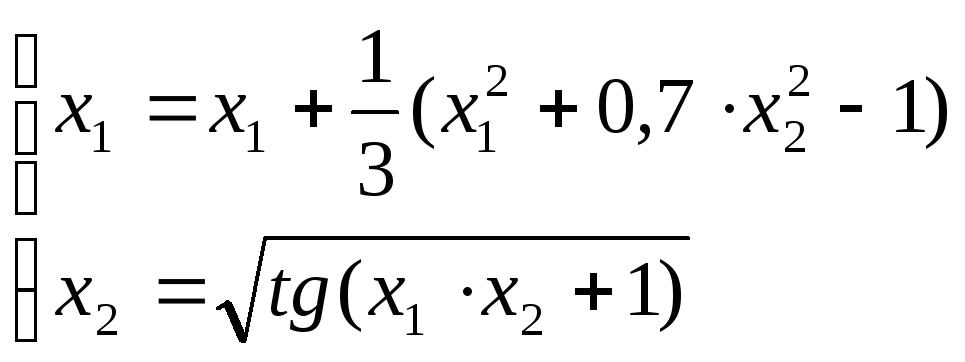
Определим частные производные:

Проверим условия сходимости в окрестности первого решения, взяв точку из области существования этого решения х₁=-0,7; х₂=0,7.

Условия сходимости соблюдаются, следовательно полученную эквивалентную систему можно использовать для уточнения четвертого решения.

3. Решение системы с помощью пакета MathCAD

4. Текст программы.

//----------------------------------------------------------------

#include <vcl.h>

#include <math.h>

#pragma hdrstop

#include "Unit1.h"

//----------------------------------------------------------------#pragma package(smart_init)

#pragma resource "*.dfm"

TForm1 *Form1;

//----------------------------------------------------------------

__fastcall TForm1::TForm1(TComponent* Owner)

: TForm(Owner)

{

}

//----------------------------------------------------------------

float x1(float x[2]){

return sqrt(1-0.7*x[1]*x[1]);}

float x2(float x[2]){

return (x[1]+tan(x[0]*x[1]+1)-x[1]*x[1]);}

//----------------------------------------------------------------

void __fastcall TForm1::Button1Click(TObject *Sender)

{

float x[2],y[2],E,q; int n=2,kmax,k;

x[0]=StrToFloat(Edit1->Text);

x[1]=StrToFloat(Edit2->Text);

E=StrToFloat(Edit3->Text);

kmax=StrToInt(Edit4->Text);

k=0;

do{

k=k+1;

for (int i=0;i<2;i++) y[i]=x[i];

if(x[1]<=-1) {

x[0]=x[0]+2.0/3*(x[0]*x[0]+0.7*x[1]*x[1]-1);

x[1]=-sqrt(tan(x[0]*x[1]+1)); }

if(x[1]>-1 && x[1]<=0) {

x[0]=sqrt(1-0.7*x[1]*x[1]);

x[1]=-sqrt(tan(x[0]*x[1]+1)); }

if(x[1]>=0 && x[1]<1) {

x[0]=x[0]+1.0/3*(x[0]*x[0]+0.7*x[1]*x[1]-1);

x[1]=sqrt(tan(x[0]*x[1]+1)); }

if(x[1]>=1) {

x[0]=x[0]-1.0/3*(x[0]*x[0]+0.7*x[1]*x[1]-1);

x[1]=sqrt(tan(x[0]*x[1]+1)); }

q=1.0/n*(fabs(x[0]-y[0])+fabs(x[1]-y[1])); }

while(q>E && k<kmax);

AnsiString f;

Memo1->Lines->Add("x1 = "+f.sprintf(" %5.10f", x[0]));

Memo1->Lines->Add("x2 = "+f.sprintf(" %5.10f", x[1]));

Memo1->Lines->Add("Достигнутая точность = "+f.sprintf(" %5.10f", q));

Memo1->Lines->Add("Количество итераций: "+IntToStr(k));

}

//----------------------------------------------------------------

5. Результаты расчётов, выполненные с помощью

подготовленной программы на Си.

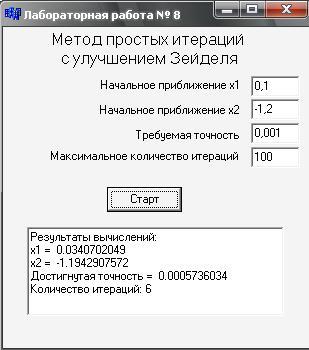
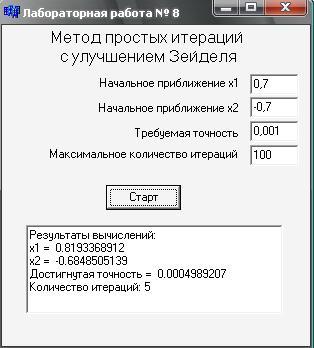
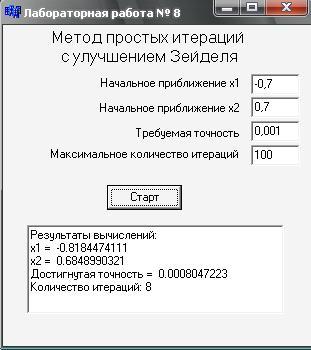
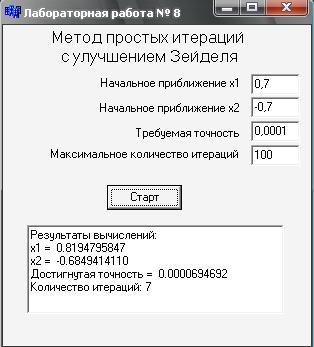
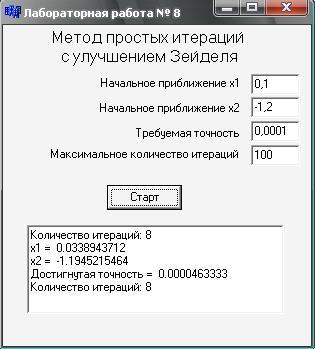
6. Выводы

Анализ результатов показывает, что программа работает правильно и верно находит корни системы нелинейных уравнений. При увелечении точности увеличивается количество итераций, а при более близком к точному начальном приближении сходимость происходит быстрее и, следовательно, количество итераций уменьшается.