ЛИСТ ДЛЯ ЗАМЕЧАНИЙ
СОДЕРЖАНИЕ
ЛИСТ С ЗАДАНИЯМИ 3
ВВЕДЕНИЕ 6
1 ТЕОРЕТИЧЕСКАЯ ЧАСТЬ 7
2 ПРАКТИЧЕСКАЯ ЧАСТЬ 11
2.1 Задача 1 11
2.2 Задача 2 11
2.3 Задача 3 12
2.4 Задача 4 13
2.5 Задача 5 14
2.6 Задача 6 15
2.7 Задача 7 16
2.8 Задача 8 16
2.9 Задача 9 17
2.10 Задача 10 17
ПРИЛОЖЕНИЕ А 20
ЗАКЛЮЧЕНИЕ 21
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ 22
Лист с заданиями
Задача 1:
Вычислить определенный интеграл
а)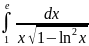 ;
;
б) ;
;
в)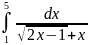 .
.
Задача 2:
Вычислить несобственный интеграл или доказать его расходимость
а)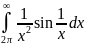 ;
;
б)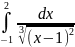 .
.
Задача 3:
Найти площадь фигуры, ограниченной указанными линиями:
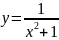 ,
,
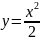 .
.
Задача 4:
Найти площадь фигуры, ограниченной указанными линиями:
 ,
,
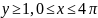 .
.
Задача 5:
Найти площадь фигуры, ограниченной указанными линиями:
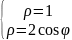 ,
,
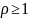 .
.
Задача 6:
Найти площадь фигуры ограниченной указанной линией:
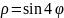 .
.
Задача 7:
Вычислить длину дуги ограниченной данными линиями:
,
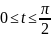 .
.
Задача 8:
Вычислить объем тела, образованного вращением фигуры ограниченной графиками функции:
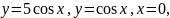
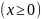 (относительно
Ox).
(относительно
Ox).
Задача 9:
Вычислить площадь поверхности, образованной вращением кривой вокруг указанной оси:
,
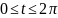 (относительно Ox).
(относительно Ox).
Задача 10:
Вычислить приближенно определенный интеграл, используя формулу Симпсона:
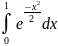 .
.
Введение
В работе я попробую найти площадь плоских фигур, площадь поверхности вращения, длину дуги и объем тела с помощью определенных интегралов, приближенное значение определенного интеграла с помощью формулы Симпсона и попытаюсь доказать одну из используемых формул.
1 Теоретическая часть
Для решения поставленных задач я воспользуюсь таблицей интегралов (приложение А), рядом формул и свойствами определенных интегралов для нахождения определенных интегралов, а именно (a и b – пределы интегрирования, F –первообразная от f):
Формула Ньютона-Лейбница (все задачи):
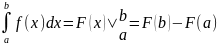 ;
;
Если
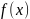 - четная, то
- четная, то
 (задача 3);
(задача 3);Формула по частям (задача 1(б)):
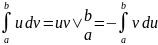 ;
;Замена переменной (задача 1(в)):
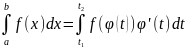 ,
где
,
где
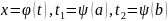 [1];
[1];Формула для нахождения несобственного интеграла первого рода (задача 2 (а)):
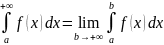 ;
;Формула для нахождения несобственного интеграла второго рода (функция f(x) имеет разрыв в точке
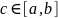 )
(задача 2 (б)):
)
(задача 2 (б)):
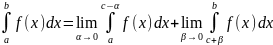 ;
;Формула для нахождения площади плоских фигур в декартовой системе координат y = y(x) (см. рисунок 1) (задача 3):
 ;
;
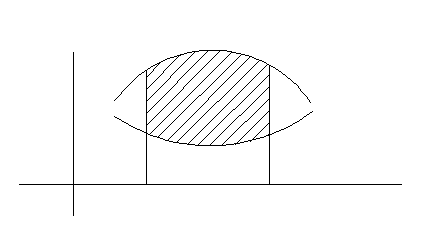
Рисунок 1
Формула для нахождения площади плоских фигур при параметрическом задании функции (задача 4):
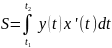 ,
где
,
где
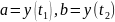 (важен порядок получения пределов
интегрирования) [2];
(важен порядок получения пределов
интегрирования) [2];Формула для нахождения площади плоских фигур в полярной системе координат
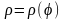 (см. рисунок 2) (задача 5):
(см. рисунок 2) (задача 5):
 ;
;
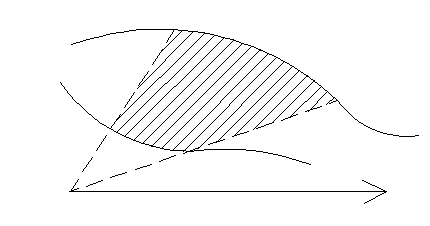
Рисунок 2
Формула для нахождения площади плоских фигур в полярной системе координат (см. рисунок 3) (задача 6):
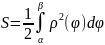 ;
;
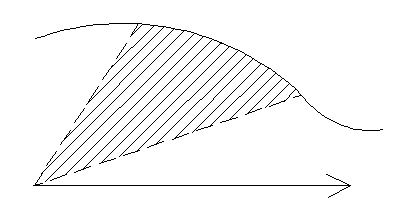
Рисунок 3
Формула для нахождения длины дуги при параметрическом задании функции (задача 7):
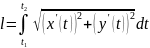 (в порядке увеличения пределов
интегрирования);
(в порядке увеличения пределов
интегрирования);Формула для нахождения объема тела вращения в декартовой системе координат (см. рисунок 4) (задача 8):
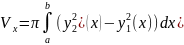 ,
,
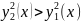 ;
;
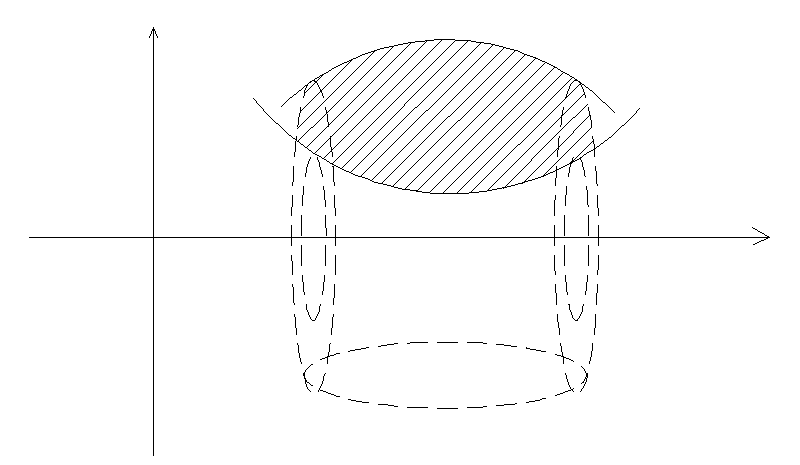
Рисунок 4
Формула для нахождения площадь поверхности вращения при параметрическом задании функции (задача 9):
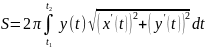 [3];
[3];Формула Симпсона [4] для нахождения приближенного значения определенного интеграла (задача 10):
 ,
,
где
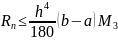 ,
,
 - предельная
абсолютная погрешность,
- предельная
абсолютная погрешность,
n=2k - шаг;
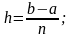
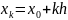 (k
= 0, 1,…, n)
(k
= 0, 1,…, n)
Значения y берем из таблицы 1:
|
|
|
|
|
|
… |
… |
|
|
|
|
Таблица 1
Докажем формулу №10: .
Пусть
 –
непрерывная функция при
–
непрерывная функция при
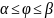 и кривая задана уравнением
и кривая задана уравнением
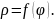 Покажем на рисунке 5 эту кривую и найдем
площадь сектора ОАВ. Для этого разобьем
сектор радиус-векторами на n
частей:
Покажем на рисунке 5 эту кривую и найдем
площадь сектора ОАВ. Для этого разобьем
сектор радиус-векторами на n
частей:
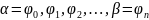 .
Пусть
.
Пусть
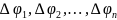 – углы между радиус-векторами. Обозначим
через
– углы между радиус-векторами. Обозначим
через
 – длину какого-либо радиус-вектора
соответствующего угла
– длину какого-либо радиус-вектора
соответствующего угла
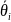 ,
заключенного между
,
заключенного между
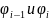 (см. рисунок 6).
(см. рисунок 6).
Рисунок 5 Рисунок 6
Площадь кругового
сектора с радиусом
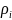 находится по формуле
находится по формуле
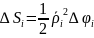 ,
,
при
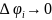
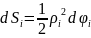 ,
,
проинтегрируем
полученное равенство в пределах от
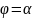 до
до
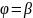 и получим искомую площадь
[5].
и получим искомую площадь
[5].
2 ПРАКТИЧЕСКАЯ ЧАСТЬ
2.1 Задача 1
а)

Ответ:
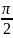 .
.
б)
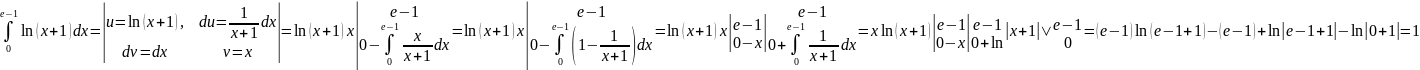 ;
;
|
x |
x+1 |
|
x+1 |
1 |
|
-1 |
|
Ответ: 1.
в)
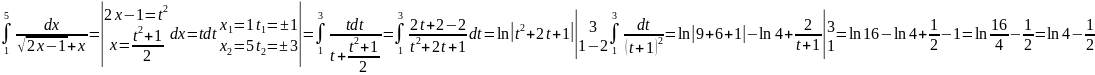 ;
;
Ответ:
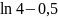 .
.
2.2 Задача 2
а)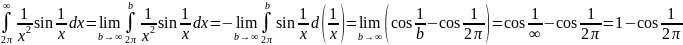 ;
;
Ответ: Несобственный интеграл сходится.
б)
 (несобственный интеграл второго рода,
функция имеет разрыв в точке 1)
(несобственный интеграл второго рода,
функция имеет разрыв в точке 1)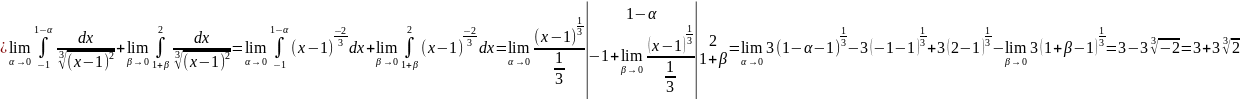 ;
;
Ответ: Несобственный интеграл сходится.
2.3 Задача 3
x |
-2 |
-1 |
0 |
1 |
2 |
y |
1/5 |
1/2 |
1 |
1/2 |
1/5 |
x |
-2 |
1 |
0 |
1 |
2 |
y |
2 |
1/2 |
0 |
1/2 |
2 |
Построим графики функций (рисунок 7).
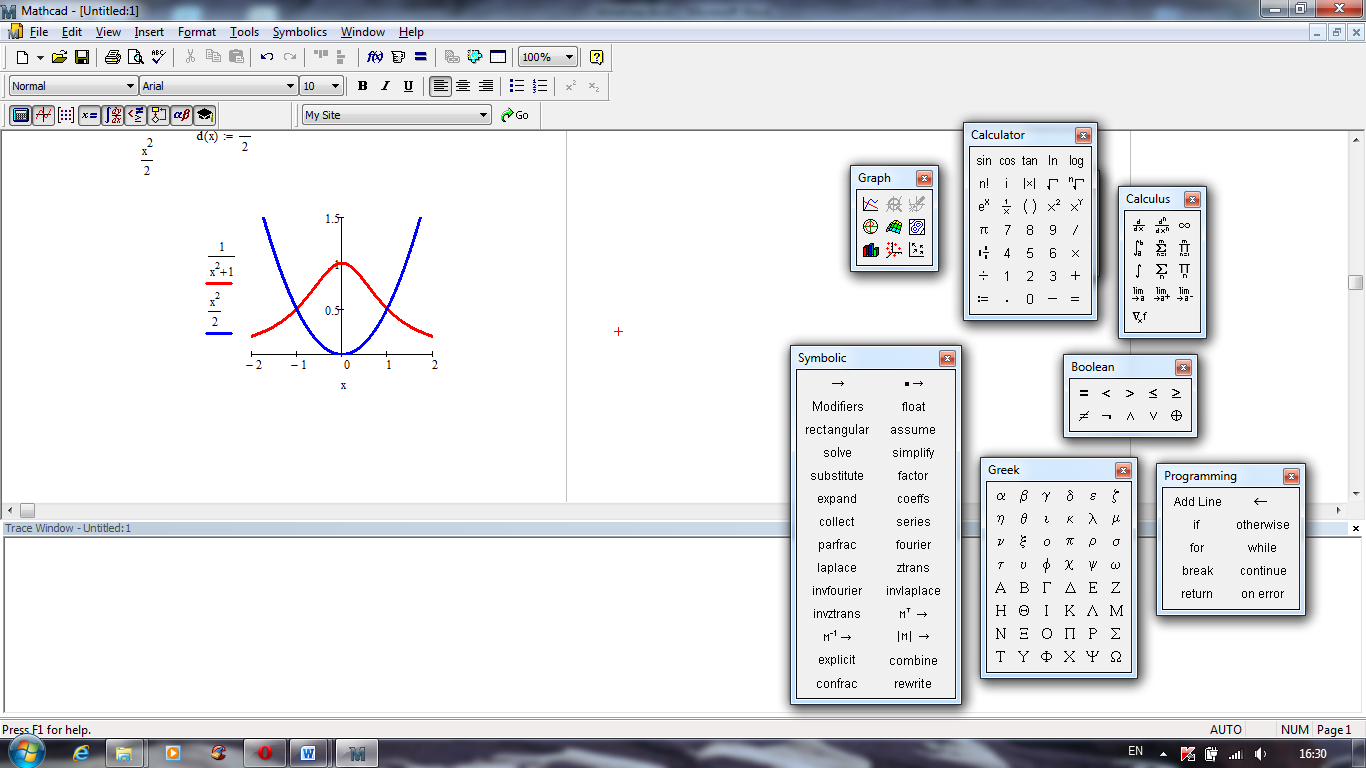
Рисунок 7
Найдем площадь (S) заштрихованной области (рисунок 7).
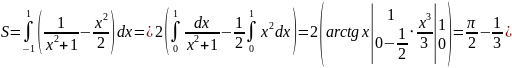 (ед2);
(ед2);
Ответ:
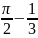 (ед2)
(ед2)

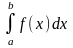
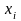 =а
=а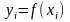
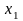 =
=