1.7. Примеры на условный экстремум с закреплёнными границами. Применение системы уравнений Эйлера-Лагранжа

1.7.1. Связи заданы в виде дифференциальных уравнений

Такие задачи часто встречаются в теории автоматического регулирования. Например, известный метод аналитического конструирования регуляторов базируется на условном экстремуме.

Пример 1.4. Синтез оптимального регулятора для осциллирующего объекта:

, (1.62)

где x(t) – управляемая величина; U – управление (управляющее воздействие), U=k ω₀²;T – постоянная времени; ε – относительное затухание; ω₀=1/T  угловая частота; k – коэффициент передачи.

В качестве критерий оптимизации примем квадратичный критерий качества:

,

где q₁≥0, q₂≥0, r>0 – некоторые весовые коэффициенты.

Зададимся граничными условиями:

при х=0

Уравнение объекта (1.62) представим системой двух уравнений:

. (1.63)

Из системы (1.63) находим связи в виде дифференциальных уравнений:

Составляем вспомогательный функционал:

Система уравнений Эйлера-Лагранжа (1.54) для данной задачи будет иметь вид:

.

В результате имеем:

. (1.64)

Из последнего уравнения (1.64) выделим управление:

и подставим его во второе уравнение системы (1.64):

. (1.65)

Запишем характеристическое уравнение системы (1.65):

(1.66)

Введём обозначение:

;

В зависимости от соотношений В и С будут иметь следующие случаи.

Случай 1. В²≥С, тогда при В>0 все корни уравнения (1.66) будут чисто мнимые и оптимальный регулятор не существует.

При В<0, корни будут: , где .

Общее решение системы (1.65) запишется:

.

Согласно граничным условиям (1.63) постоянные .

Производную выразим через переменные состояния

(1.67)

С учётом второго уравнения системы (1.64) и уравнения (1.67) получаем алгоритм оптимального управления:

Структурная схема замкнутой системы приведена на рис.1.7.

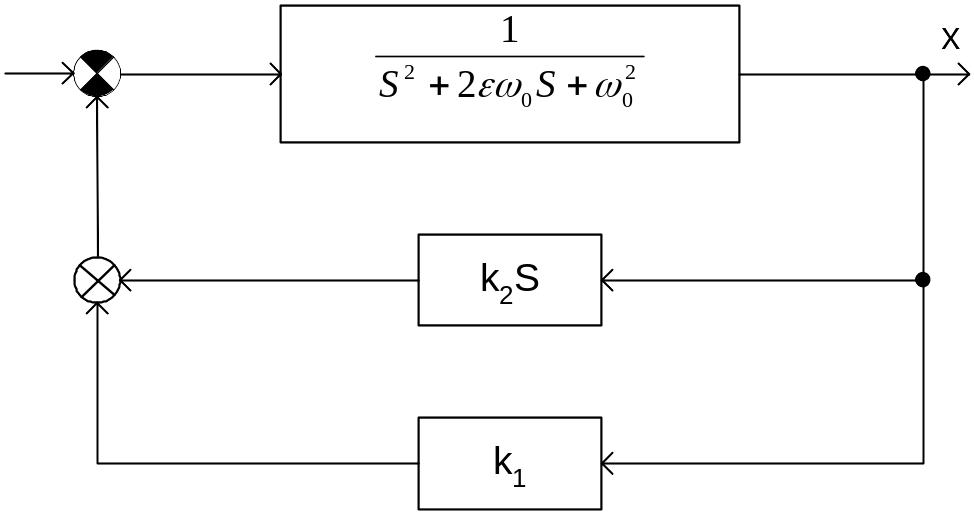
Рис. 1.7 Структурная схема оптимальной системы автоматического управления.

На структурной схеме приняты обозначения: ;

Случай 2. В случае, когда В²<С корни характеристического уравнения получаются комплексно-мнимыми:

, ,

где , .

Для этого случая: и .

1.7.2. Связи заданы в виде интегральных уравнений

Исторически первой задачей, известной в глубокой древности и отнесённой в последствии к задачам вариационного исчисления, явилась так называемая задача Дидо. Легенда гласит, что Дидо (Др. грек. Дидона) – царица одного из государств Древней Греции, преследуемая царём соседнего государства, бежала в Северную Африку и попросила у местного населения участок земли, который можно охватить шкурой вола. Получив согласие на столь ничтожную просьбу, она на глазах у изумлённых зрителей разрезала шкуру на тонкие ремешки и, связав, их друг с другом, охватила полученной нитью изрядный по тем временам участок, на котором основала знаменитый в древности город Карфаген. Сейчас на месте этого города расположен город Тунис.

Уже античные учёные заинтересовались математической стороной этой легенды. Допустим, что нить длинной ℓ уже связана, как её надо расположить, чтобы охваченный ею участок имел наибольшую площадь?

Приступим к формулировке задачи Дидо и её решению.

Пример 1.5. Среди всех кривых ℓ, соединяющих две точки А и В найти кривую, ограничивающую, совместно с отрезком [АВ], наибольшую площадь (рис. 1.8).

Рис. 1.8. Геометрическое представление задачи Дидо.

Расположим координатные оси так, чтобы ось 0Х проходила через точки А и В.

В результате получаем площадь, ограниченную искомой кривой y(x):

. (1.68)

Требуется найти функцию y(x), доставляющую максимум интегралу (1.68), при условии

(1.69)

и условиях на концах отрезка:

.

Запишем интеграл (1.69) с учётом (1.25):

, .

Введём промежуточную функцию (1.53):

и образуем вспомогательный функционал (1.68):

Подынтегральная функция L явно не зависит от х, поэтому пишем сразу первый интеграл уравнения Эйлера:

,

то есть

.

Тогда или .

Выразим

(1.70)

Проинтегрировав выражение (1.70), получим

(1.71)

И далее путём преобразования (1.71) получили уравнение окружности с радиусом λ₀:

.

Теперь можно оценить размер участка земли царицы Дидо. Пусть шкура вола имела площадь 4 м² и царица Дидо разрезала её на ремешки шириной 0,5 см, тогда длина нитки ℓ составила: ℓ=800м, а площадь участка S=800²/4π=50930м², т.е. примерно 5Га. На такой площади можно было основать город и греческая легенда, во всяком случае, правдоподобна.

Если же Дидо расположила бы ремень по контуру квадрата, то площадь получилась бы: S=40000м², что почти на 22% меньше.

Оглавление

Введение 3

1. Классическое вариационное исчисление 5

1.1. Понятие вариационного исчисления 5

1.2. Экстремум функционала. Необходимое и достаточное условия экстремума 5

1.2.1. Приращение функционала 6

1.2.2. Необходимое условие экстремума функционала 6

1.2.3. Достаточное условие локального экстремума 7

1.3. Вариационная задача на безусловный экстремум с закреплёнными границами 7

1.3.1. Вывод первой и второй вариации интегрального типа для простейшего функционала 8

1.3.2. Вывод уравнения Эйлера 9

1.3.3. Условие Лежандра 10

1.3.4. Обсуждение уравнения Эйлера 10

1.3.5. Примеры на безусловный экстремум с закреплёнными границами. Применение уравнения Эйлера 12

1.4. Функционалы, зависящие от нескольких функций 16

1.5. Функционалы, зависящие от старших производных 17

1.6. Вариационные задачи на условный экстремум 19

1.6.1. Вариационные задачи на условный экстремум, когда связи представлены конечными равенствами 20

1.6.2. Вариационные задачи на условный экстремум, когда условия представлены дифференциальными уравнениями 20

1.6.3. Вариационные задачи на условный экстремум со связями в виде интегральных уравнений 21

1.7. Примеры на условный экстремум с закреплёнными границами. Применение системы уравнений Эйлера-Лагранжа 22

1.7.1. Связи заданы в виде дифференциальных уравнений 22

1.7.2. Связи заданы в виде интегральных уравнений 24

4