1.2.3. Достаточное условие локального экстремума
Теорема 1.3. Пусть функционал I(y) дважды дифференцируемый в области G и имеют место условия:
а) первая вариация функционала на кривой y0(x) равна нулю, т.е. δI(y0,h) ≡ 0;
б) вторая вариация на кривой y0(x) сильно положительна, т.е. δ2I(y0,h)≥k ׀׀h׀׀2 , где k>0 – некоторое число,
тогда функционал I(y) достигает на кривой минимума.
Доказательство теорем 1.1, 1.2 и 1.3 дано в [7].
1.3. Вариационная задача на безусловный экстремум с закреплёнными границами
Рассмотрим простейший функционал (1.3).
Подынтегральная
функция
должна быть
непрерывно-дифференцируема до второго
порядка по всем аргументам. Экстремум
функционала будем определять среди
функций y(x)
на интервале
[x1,x2]
и удовлетворяющим условиям: y(x1)
= y1
, y(x2)
= y2.
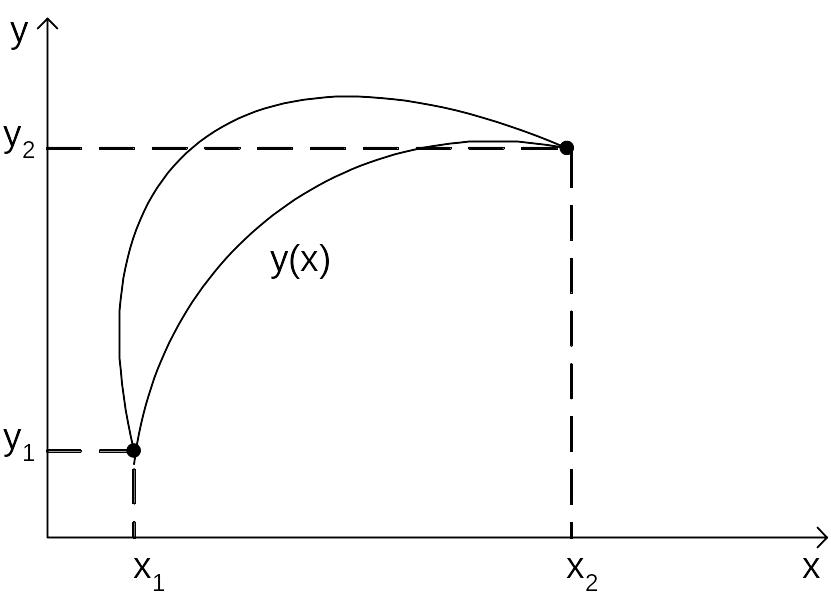
Рис. 1.2. Задача с закреплёнными границами для простейшего функционала.
При выполнении этих условий все рассматриваемые кривые y(x) будут проходить через две фиксированные точки (x1, y1) и (x2, y2). Такая задача является простейшей задачей вариационного исчисления и называется задачей с закреплёнными границами или двухточечной задачей.
1.3.1. Вывод первой и второй вариации интегрального типа для простейшего функционала
Вывод вариаций осуществляется в классе непрерывных гладких функций, т.е. функций не только непрерывных, но и имеющих непрерывную первую производную.
Постановка задачи. Дано:
функционал: 
; (1.5)
начальная точка (x1, y1) и конечная точка (x2, y2).
Далее предполагаем, что нашли кривую, которая минимизирует функционал.
После этого применяют приращение функции и получают вариацию функционала:
δI = Iв Iи , (1.6)
где
(1.7)
варьируемый
функционал за счёт приращений функций
и
;
функционал
(1.8)
исходный функционал.
Подставим (1.7) и (1.8) в (1.6):
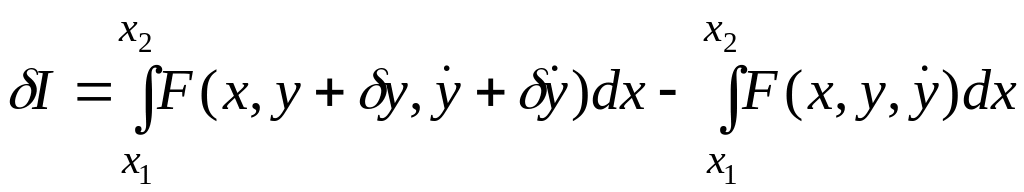(1.9)
Из выражения (1.9) можно вывести первую и вторую вариации. Для этого раскладываем варьируемую подынтегральную функцию в ряд Тейлора:
(1.10)
Выражение в квадратных скобках характеризует первую вариацию, выражение в фигурных скобках – вторую вариацию.
Теперь отбросим вторую вариацию и остаточный член Rn в выражении (1.10) и оставшуюся часть подставим в первый интеграл выражения (1.9), получаем первую вариацию интегрального типа:
(1.11)
Полученная первая вариация равна нулю согласно теореме 1.
Из выражения (1.11) можно найти кривую y(x), удовлетворяющую экстремуму функционала (1.5).
1.3.2. Вывод уравнения Эйлера
В выражении второе слагаемое можно упростить путём интегрирования по частям:
(1.12)
Первое слагаемое первой части выражения (1.12) равно нулю, т.к. кривые y(x) проходят через закреплённые границы.
Тогда первая вариация (1.11) принимает вид:
(1.13)
Теперь применим лемму Лагранжа, которая утверждает: если непрерывная функция М(х) обладает тем свойством, что
для
любой гладкой функции у(х),
то обязательно будем иметь М(х)=0
для всех х(
)
[10].
В соответствии с леммой Лагранжа равенство (1.13) будет справедливо при выполнении условия:
(1.14)
Полеченное уравнение (1.14) является уравнением Эйлера.
С помощью этого уравнения ищутся экстремали, то есть кривые y(x), которые обращают в нуль левую часть уравнения (1.14).
Уравнение Эйлера (1.14) является уравнением второго порядка. Оно легко решается в некоторых частных случаях, однако решения для общего случая не существует.
В вариационном исчислении, как правило, имеют дело только с первой вариацией. В связи с этим рассматриваемый метод даёт только необходимое условие экстремума (нельзя сразу ответить, какой экстремум найден: максимум или минимум).
Для получения ещё и достаточного условия надо исследовать вторую вариацию.
Второе необходимое условие экстремума функционала в простейшей задаче вариационного исчисления определяется с помощью второй вариации, выражение которой представлено в фигурных скобках выражения (1.10):
(1.15)
Интегрируем по частям второе слагаемое подынтегральной функции (1.15), получим:
Если δ2I ≥0, то получен минимум функционала (1.5), если δ2I ≤0, то – максимум функционала (1.5).
Кроме второй вариации существует ещё условие Лежандра для исследования экстремума функционала на минимум и максимум.