1.4. Функционалы, зависящие от нескольких функций

В более сложных задачах встречаются функционалы, зависящие от нескольких функций и их первых производных:

при заданных граничных условиях для всех функций.

Первая вариация экстремума функционала имеет вид:

Необходимым условием экстремума функционала является обращение в нуль его первой вариации. Учитывая независимость приращений h_i и, варьируя по очереди каждую из функций при фиксированных остальных, приходим к системе уравнений ЭйлераЛагранжа:

Второе необходимое условие минимума функционала имеет вид:

для любых допустимых приращений h_i, где ; ; ; .

1.5. Функционалы, зависящие от старших производных

Рассмотрим необходимые условия экстремума функционала:

Рассматриваются функционалы, где F – непрерывная функция, дифференцируемая n+2 раза по всем аргументам. В качестве допустимых используются функции y(x), дифференцируемые 2n раз, а в граничных точках задаются значения самой функции и её производных до (n-1) включительно, то есть:

.

С помощью рассуждений, аналогичных тем, которые были использованы при выводе уравнения Эйлера (равенство нулю первой вариации), можно получить необходимое условие экстремума функционала:

(1.41)

Уравнение (1.41) называется уравнением Эйлера-Пуассона. Это уравнение является дифференциальным уравнением порядка 2n. Его общее решение содержит 2n произвольных постоянных для использования, которых необходимо 2n граничных условий.

Рассмотрим пример применения уравнения Эйлера-Пуассона для определения оптимального процесса, при котором минимизируется расход энергии на управление.

Пример 1.4. Минимизировать расход энергии на управление астатическим объектом из двух интегрирующих звеньев:

(1.42)

Здесь x(t) – управляемая переменная, являющаяся искомой функцией, на которой функционал достигает экстремума; U(t) – управление (управляющее входное воздействие); T_u – постоянная интегрирования. Примем T_u=1.

Заданы граничные условия:

при времени t=0: ;

при конечном времени t=T: .

Требуется найти такую траекторию движения x(t) и закон управления U(t), при котором минимизируется функционал:

или с учётом (1.42):

(1.43)

Подынтегральная функция F зависит только от второй производной искомой функции x(t):

(1.44)

Для данного примера уравнение Эйлера-Пуассона примет вид:

(1.45)

С учётом (1.44) получим:

Подставим полученные выражения в (1.45) и дважды продифференцируем по аргументу времени t:

Интегрируя это выражение два раза, определяем оптимальный закон изменения управляющего воздействия:

(1.46)

Чтобы найти оптимальную траекторию движения x(t) проинтегрируем (1.46) ещё два раза. В результате получим:

Постоянные интегрирования С₁ С₄ определяются из граничных условий.

Проверяем выполнение условия Лежандра:

.

Следовательно, на найденной экстремали x(t) реализуется минимум функционала (1.43).

Для рассмотренного объекта второго порядка оптимальный закон управления (1.46) получается линейным (рис. 1.6).

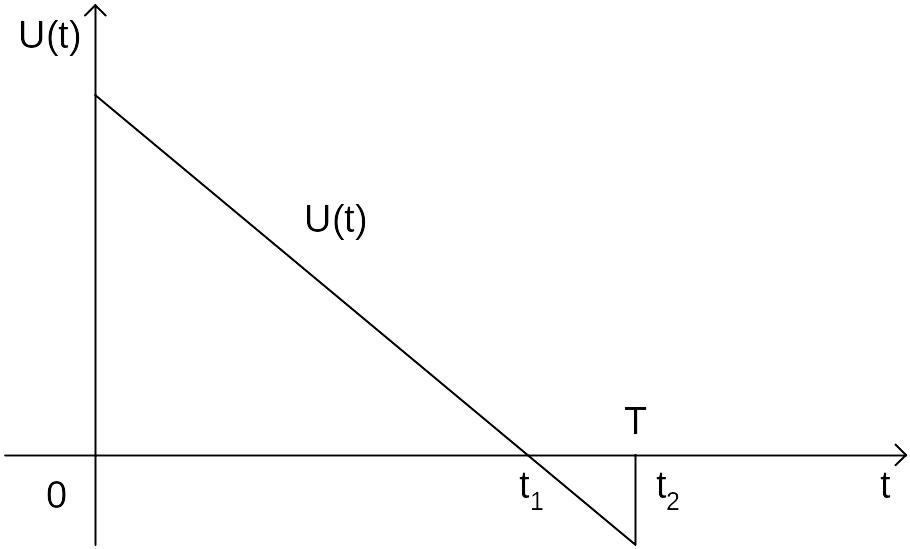
Рис. 1.6. Геометрическая трактовка найденного закона управления, минимизирующий расход энергии.