2В) Проверить распределение на нормальность можно путем расчета показателей асимметрии первого, второго и третьего порядков и показатель эксцесса.
Исследуем близко ли распределение факторного признака к нормальному.
Таблица 3. Расчетные величины.
№ |
Х |
|
(Хi-Xср) |
(Хi-Xср)^2 |
(Хi-Xср)^3 |
(Хi-Xср)^4 |
|||||
28 |
10,127 |
|
-5,00998341 |
25,09993379 |
-125,750252 |
630,006676 |
|||||
29 |
16,61 |
|
1,47273659 |
2,168953058 |
3,194296527 |
4,70435737 |
|||||
30 |
20,325 |
|
5,18712659 |
26,90628224 |
139,566292 |
723,948024 |
|||||
31 |
11,483 |
|
-3,65438341 |
13,35451812 |
-48,8025295 |
178,343154 |
|||||
32 |
20,23 |
|
5,09256659 |
25,93423446 |
132,0718159 |
672,584517 |
|||||
36 |
13,493 |
|
-1,64454341 |
2,704523033 |
-4,44770554 |
7,31444484 |
|||||
39 |
21,697 |
|
6,55974659 |
43,0302753 |
282,2677016 |
1851,60459 |
|||||
40 |
16,208 |
|
1,07073659 |
1,146476841 |
1,227574702 |
1,31440915 |
|||||
42 |
20,944 |
|
5,80638659 |
33,71412521 |
195,7572445 |
1136,64224 |
|||||
43 |
15,406 |
|
0,26850659 |
0,072095788 |
0,019358194 |
0,0051978 |
|||||
44 |
11,607 |
|
-3,52995341 |
12,46057109 |
-43,9852354 |
155,265832 |
|||||
45 |
11,52 |
|
-3,61743341 |
13,08582449 |
-47,3370987 |
171,238803 |
|||||
46 |
6,9318 |
|
-8,20561541 |
67,33212429 |
-552,501517 |
4533,61496 |
|||||
48 |
11,314 |
|
-3,82370341 |
14,62070778 |
-55,9052502 |
213,765096 |
|||||
49 |
17,321 |
|
2,18346659 |
4,767526342 |
10,40973448 |
22,7293074 |
|||||
50 |
15,479 |
|
0,34160659 |
0,116695061 |
0,039863802 |
0,01361774 |
|||||
51 |
16,64 |
|
1,50273659 |
2,258217254 |
3,393505691 |
5,09954516 |
|||||
Итого |
257,34 |
|
5,3291E-15 |
288,7730841 |
-110,782201 |
10308,1948 |
|||||
Ср.знач |
15,137 |
|
Х |
Х |
Х |
х |
|||||
Рассчитаем показатели медианы, ассиметрии и эксцесса:
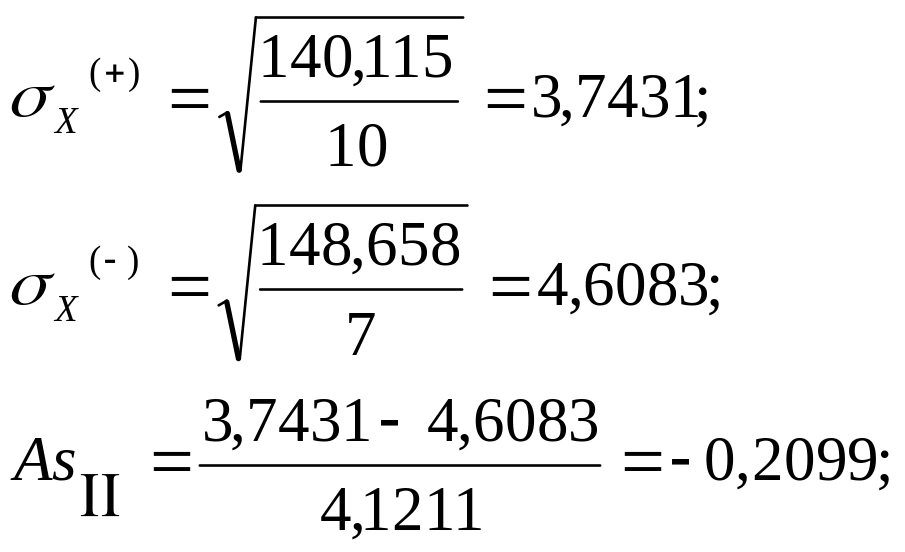
Рассчитаем асимметрию третьего порядка:
Найдем значение эксцесса:
Теперь проверим, подчиняется ли распределение результативного признака нормальному закону.
Таблица 4. Расчетные величины
№ |
У |
(Уi-Уср) |
(Уi-Уср)^2 |
(Уi-Уср)^3 |
(Уi-Уср)^4 |
28 |
253,6498 |
-50,34906 |
2535,027843 |
-127636,269 |
6426366,16 |
29 |
413,3492 |
109,35034 |
11957,49686 |
1307556,347 |
142981731 |
30 |
435,9925 |
131,99364 |
17422,321 |
2299635,566 |
303537269 |
31 |
289,801 |
-14,19786 |
201,5792286 |
-2861,99367 |
40634,1854 |
32 |
317,7906 |
13,79174 |
190,2120922 |
2623,355721 |
36180,64 |
36 |
462,2961 |
158,29724 |
25058,01619 |
3966614,803 |
627904175 |
39 |
479,7696 |
175,77074 |
30895,35304 |
5430499,066 |
954522839 |
40 |
333,6026 |
29,60374 |
876,381422 |
25944,16776 |
768044,397 |
42 |
214,2828 |
-89,71606 |
8048,971422 |
-722122,003 |
64785941 |
43 |
324,5566 |
20,55774 |
422,6206739 |
8688,125933 |
178608,234 |
44 |
274,5077 |
-29,49116 |
869,7285181 |
-25649,3029 |
756427,695 |
45 |
239,3227 |
-64,67616 |
4183,005672 |
-270540,744 |
17497536,5 |
46 |
116,4529 |
-187,54596 |
35173,48711 |
-6596645,41 |
1237174196 |
48 |
296,1518 |
-7,84706 |
61,57635064 |
-483,193318 |
3791,64696 |
49 |
290,4255 |
-13,57336 |
184,2361017 |
-2500,70293 |
33942,9412 |
50 |
246,5045 |
-57,49436 |
3305,601432 |
-190053,439 |
10927000,8 |
51 |
179,5247 |
-124,47416 |
15493,81651 |
-1928579,79 |
240058350 |
Итого |
5167,9806 |
-2E-05 |
156879,4315 |
3174488,582 |
3607633035 |
Ср.знач |
303,99886 |
Х |
Х |
х |
х |
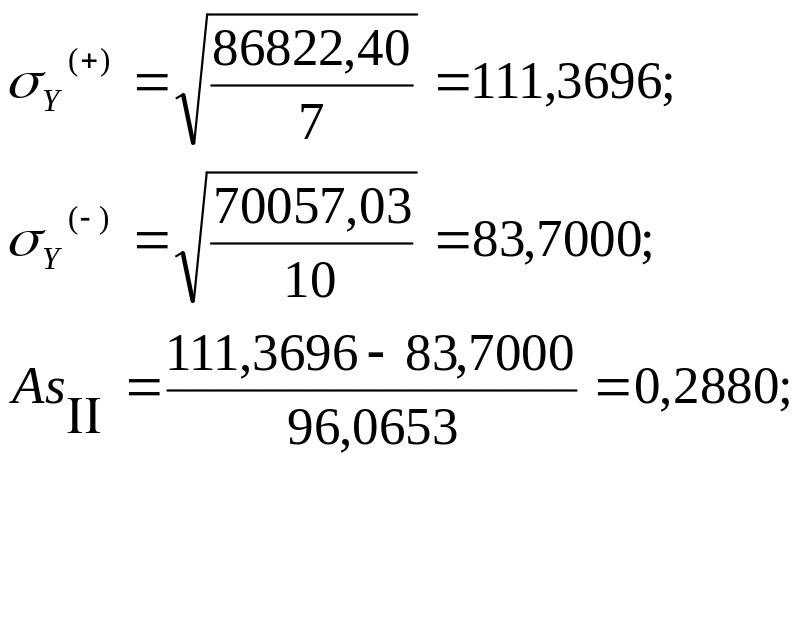
Рассчитаем асимметрию третьего порядка:
Найдем значение эксцесса:
Полученные данные позволяют сделать следующий вывод. Значения асимметрии первого, второго, третьего порядков и эксцесса достаточно малы, мода, медиана и среднее значение результативного признака приближенно равны, следовательно, совокупность подчиняется нормальному закону.
2г) Оценим модель через среднюю ошибку аппроксимации.
Средняя ошибка
аппроксимации – среднее отклонение
расчетных значений от фактических.
Допустимый предел значений
- не более 8 – 10%.
=
=
431,421/17=25,37%
В среднем расчетные значения отклоняются от фактических на 25,37%. Это значение значительно превышает допустимый предел, следовательно качество построенной модели невысокое. Это, а также небольшое значение коэффициента детерминации говорит о том, что линейный тип модели не достаточно хорошо отражает представленные эмпирические данные.
2д) Для оценки силы связи признаков у и х найдем средний коэффициент эластичности:
Средний коэффициент
эластичности
показывает, на сколько процентов в
среднем по совокупности изменится
результат y
от своей средней величины при изменении
фактора x
на 1% от своего среднего значения:
.=
=
=0,5690
Таким образом, в среднем на 0,5% по совокупности изменится валовая продукция от своей средней величины при изменении среднегодового заработка на 1%.
Бета-коэффициент:
показывает, что среднеквадратическое отклонение валовой продукции изменится в среднем на 49% от своего среднего значения при изменении среднегодового заработка на величину ее среднеквадратического отклонения.