
Вопрос 20
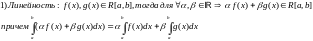



//


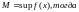


Теорема о достижимости верхней и нижней грани значений (45)
Теорема
Ф-ия , непрерывная на компакте, достигает на нем точную верхнюю и точную низнюю грани мн-ва своих значений
Пусть
 Предположим
противное :
Предположим
противное :

Рассмотрим ф-ию
 Тогда
по пред.теореме
Тогда
по пред.теореме
 -огр.на
мн-ве D. След-но , найдется
-огр.на
мн-ве D. След-но , найдется
 т.ч.
т.ч.

След-но,

Это противоречит
тому, что

Для точной нижней гране док-во аналогично
Вопрос № 9
Теорема (о замене переменной в неопределенном интеграле) :
Пусть дана ф-ия
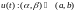
пусть
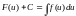
пусть
 ,
тогда :
,
тогда :
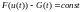
Достаточно доказать,
что
 (
из этого будет следовать, что
.
(
из этого будет следовать, что
.

Пример:

Теорема о множестве значений непрерывной (46)
Теорема :
Ф-ия , непрерывна на связном компакте принимает все свои промежуточные значения
По
пред.теореме
 т.ч.
т.ч.
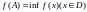 ;
;
т.к.D-
связное мн-во, то
непрерывная
кривая
 т.ч.
т.ч.
1)

2)

Р-м ф-ию
 -
фи-я одной переменной на
-
фи-я одной переменной на

Т.к.
 -непрерывна
то
-непрерывна
то

Следовательно принимает все свои промежуточные значения
*рисунок*
Вопрос 13
Опр: Выражение вида
 наз-ся простейшей дробью
наз-ся простейшей дробью
 -го
типа
-го
типа
Опр: Выражение вида
 наз-ся
простейшей дробью
наз-ся
простейшей дробью
 -го
типа
-го
типа
Опр: Выражение вида

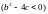 наз-ся
простейшей дробью
наз-ся
простейшей дробью
 -го
типа
-го
типа
Опр: Выражение вида
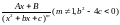 наз-ся
простейшей дробью
наз-ся
простейшей дробью
 -го
типа
-го
типа
Теорема :
Пусть многочлен
 разложен на
разложен на
 где
где
 и
и
 взаимно
простые многочлены . По док.теореме
взаимно
простые многочлены . По док.теореме

Многочлен
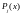 разложим
на степени :
разложим
на степени :
 .
Тогда дробь
.
Тогда дробь
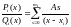 дробь
и
типов
для всех
дробь
и
типов
для всех
 .
Многочлен
.
Многочлен
 степни
степни
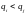 ,
разделим на
,
разделим на
 с
остатком
с
остатком
 ,
тогда
,
тогда

Вопрос 12
Опр: Многочлен
 делится
(нацело )на многочлен
,
если
многочлен
,
т.ч.
делится
(нацело )на многочлен
,
если
многочлен
,
т.ч.

Опр:Многочлен делиться на многочлен с остатком , если найдутся мн-ны и
1)

2)
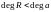 ,
где
-неполное
частное ,
,
где
-неполное
частное ,
 -остаток
-остаток
Опр: Пусть
даны многочлены
и
,
тогда многочлен
 наз-ся
их наибольшим общим делителем(НОД), если
наз-ся
их наибольшим общим делителем(НОД), если
1) делиться на
2) делиться на
3)Если -общ.делитель многочлена и , то делится на
Теорема :
ПУсть даны
многочлены
 и
,
пусть
и
,
пусть
 НОД
НОД ,
тогда сущ.многочлены
,
тогда сущ.многочлены
 и
и
 ,
т.ч.
=
*
+
*
,
т.ч.
=
*
+
*
Пусть
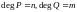
Без потери
общности

Разделим на с остатком
 причем
причем
 (1)
(1)
Разделим
на
 с
остатком
с
остатком
 причем
причем
 (2)
(2)
Разделим
на
 с
остатком
с
остатком
 причем
причем
 (3)
(3)
и т.д.


Поскольку
 ,
следовательно
,
следовательно
на каждом шаге степень остатка строго уменьшается . След-но, на некотором шаге остаток будет равен 0.
Тогда из
последнего равенства
 следует,
что
следует,
что

Подставляя
предыдущих равенств и приводя подобные
слагаемык при
и
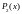 ,
приходим к равенству
,
приходим к равенству

Вопрос № 10
Теорема (Формулы интегрирования по частям)
Пусть даны
 ,тогда
,тогда
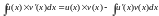


Замечание : формула интегрирования по частям записывают в дифференциальный формуле:

Примеры:
1)

2)

Теоремы сравнения для несобственных интегралов (37)
Теорема(Признаки сравнения) :
Пусть
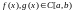 ,
пусть
,
пусть


1) Если
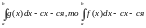
2) Если

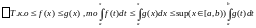

1)

2) Аналогично
Теорема (Предельный признак сравнения)
Пусть

Пусть
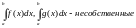



Пусть

Пусть

Вопрос № 4
Опр : Точка
наз-ся
точкой перегиба , если
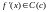 и явл-ся границей двух различных
интегралов выпуклости
и явл-ся границей двух различных
интегралов выпуклости
*дорисовать график*
Теорема (Необходимые условия перегиба)
Если
-
точка перегиба, то либо
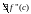 либо
либо

Если - то теорема доказана
Пусть
 -
сущ-ет и она
-
сущ-ет и она

Рассмотрим случай ,
когда


 -аналог
-аналог
, тогда по формуле Тейлора
Раз
 ,
то
,
то
 т.ч. для
будет
вып-но :
т.ч. для
будет
вып-но :
в точке ф-ия выпуклая вниз. Это противоречит тому , что в точке - точка перегиба . Значит наше предположение неверно
Формула замены переменной в определеном интервале (26)
Теорема :
Пусть дан
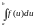 и
задана ф-ция
и
задана ф-ция
 ,
причем
,
причем
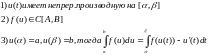
Пусть
 -некоторая
первообразная ф-ии
-некоторая
первообразная ф-ии
 на
.
Тогда по теореме о замене переменной в
неопред.интеграле :
на
.
Тогда по теореме о замене переменной в
неопред.интеграле :

Следовательно ,

Формула интегрирования по частям (26)
Пусть ф-ии
 и
и обладают
непрер-ой производной на
,
тогда
обладают
непрер-ой производной на
,
тогда

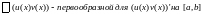 .
По формуле Н-л.:
.
По формуле Н-л.:
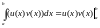
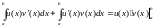
Пример :



1)

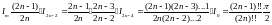
2)

