46.Метод Лагранжа. Вариации произвольных постоянных.

Пусть 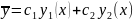– общее решение уравнения Y”+a₁(x)y’+a₂(x)y = 0. => y*=C₁(x)y₁(x)+C₂(x)y₂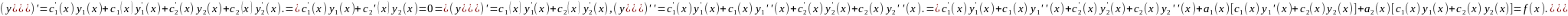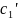(x) => => (x)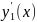 + 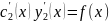. Таким образом, функция y*=C₁(x)y₁(x)+C₂(x)y₂(x) будет частным решение y* уравнения Y”+a₁(x)y’+a₂(x)y = 0, если функции c1(x) и c2(x) удовлетворяют системе уравнений 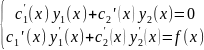. Система имеет единственное решение: 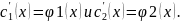Интегрируя эти функции, находим c1(x) и c2(x), а затем по формуле y*=C₁(x)y₁(x)+C₂(x)y₂(x) составляем частное решение уравнения.

47.Неоднородные ду 2ого порядка с правой частью специального вида.

ЛНДУ 2 порядка с постоянными коэффициентами: y’’+py’+qy = f(x). 1. Правая часть имеет вид f(x) = 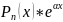, где 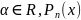– многочлен степени n. Уравнение запишется в виде: y’’+py’+qy = . В этом случае частное решение 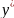ищем в виде: 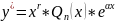, где r – число, равное кратности α как корня характеристического уравнения 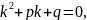а = 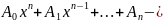многочлен степени n, записанный с неопределенными коэффициентами A_i (i=1,2,…,n). 2. 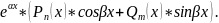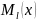Правая часть имеет вид f(x)= Уравнение запишется в виде: y’’+py’+qy = Частное решение уравнения следует искать в виде: где r – число, равное кратности α+βi как корня характеристического уравнения и 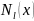- многочлены степени l с неопределенными коэффициентами, l – наивысшая степень многочленов и .
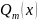