19. Необходимый признак сходимости.

Если ряд сходится, то его общий член u_n стремится к нулю, т.е.

20. Признаки сравнения знакоположительных рядов.

Теорема. Пусть даны два знакоположительных ряда и . Если для всех n выполняется неравенство 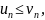то из сходимости ряда следует сходимость ряда , из расходимости первого ряда следует расходимость второго ряда. Теорема (предельный признак сравнения). Пусть даны два знакоположительных ряда и . Если существует конечный, отличный от 0, предел то ряды сходятся или расходятся одновременно.

21. Признак Даламбера и радикальный признак Коши.

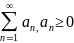
Даламбера:Пусть дан ряд 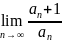=l. Тогда при l ряд раходится

Коши: Пусть дан ряд с положительными членами и существует конечный и бесконечный предел = . Тогда ряд сходится при

22.Интегральный признак Коши. Если f(n)=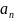 на промежутке [1;+ 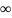), является неубывающей, тогда ряд и несобственный интеграл

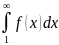
23.Функциональные ряды. Поточечная и равномерная сходимость. Ряд, членами которого являются функции от x, называется функциональным : 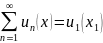+ Придавая x определенное значение 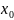, мы получим числовой ряд 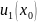+ 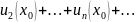, который может быть как сходящимся, так и расходящимся. Если мы зафиксируем x в к-либо точке , то получаем из функц. числовой ряд, он может сходится , а может расходиться. Если в т. X₀ – этот числовой ряд сход. то это точка сходимости.Множество всех точек сходимости ряда + называются областью сходимости этого ряда. Такая сходимость(по точкам) называется поточечной сходимостью. 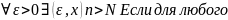малого сколь угодно 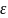сущ. │ 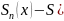x)│ Если в определении номер последовательности зависит только от и не зависит от x, то такая сходимость называется равномерной.

24.Признак Вейерштрасса. Пусть имеется функциональный ряд 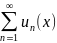с другой стороны имеется 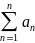, то выполняется условия: 1) │ (x)│ 2) сходится. Утверждает, что ряд сходится равномерно. Ряд называется мажорантным рядом(или просто мажорантой), а ряд - мажорируемый.

25. Свойства равномерно сходящихся рядов. 1)Если функциональный ряд сходится равномерно, то его сумма S(x)- есть функция непрерывная. 2)Для равномерного сх-ся рядов справедлив предельный переход .

26. Степенные ряды. Теорема Абеля. Степенные ряды – это ряды вида ² + … + ⁿ+ … x=0 – точка сходимости. Т.Абеля: Если степенной ряд сходится при x=x₀ 0, то он абсолютно сходится при всех значениях x, удовлетворяющих неравенству │x│<│x₀│. Следствие: если ряд расходится при x=x1, то он расходится и при всех x, удовлетворяющих неравенству │x│>│x₁│.

27. Радиус и интервал сходимости степенного ряда. Из теоремы Абеля следует, что если x₀ 0 есть точка сходимости степенного ряда, то интервал (-│ │;│ │) весь состоит из точек сходимости данного ряда; при всех значениях x вне этого интервала ряд расходится. Интервал (-│ │;│ │) и называют интервалом сходимости степенного ряда. Положив │ │=R, интервал сходимости можно записать в виде (-R;R). Число R называют радиусом сходимости степенного ряда, т.е. R>0 – это такое число, что при всех x, для которых│x│<R, ряд абсолютно сходится, а при │x│>R ряд расходится.

28. Нахождение коэффициентов тригонометрического ряда по формулам Фурье. Тригонометрическим рядом называется функциональный ряд вида , где действительные числа , называются коэффициентами ряда. Числа , , определяемые по формулам = , называются коэффициентами Фурье функции f(x), а тригонометрический ряд с таким коэффициентами – рядом Фурье функции f(x).

29.Ряд Фурье для четных и нечётеных функций. Для четных функций ряд Фурье имеет вид :

f(x) =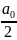 + 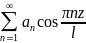, где а₀ = 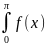dx ;a_n = dx ; b_n = 0

для нечетных функций: f(x) = 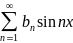, где b_n = ;a₀=0,a_n = 0

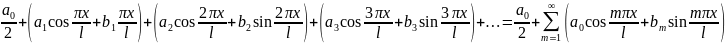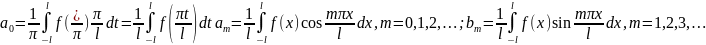30.Ряд Фурье на интервале (- ). Рядом Фурье для функции f(x) в интервале [–l, l] называется тригонометрический ряд вида с коэффициентами ряда a_m, b_m, вычисленными по формулам Фурье: Достаточные условия разложимости функции в ряд Фурье сформулированы в теореме Дирихле.Т е о р е м а. Если в интервале [–l, l] функция f (x) имеет конечное число точек разрыва первого рода (или непрерывна) и конечное число точек экстремума (или не имеет их вовсе), то ее ряд Фурье сходится, т.е. имеет сумму S (x) во всех точках указанного интервала.При этом:а) в точках непрерывности функции f (x) ряд сходится к самой функции: S (x) = f (x); b) в каждой точке разрыва xk функции f(x) ряд сходится к полусумме односторонних пределов функции слева и справа