36. Линейные ду первого порядка и уравнение Бернулли.

Дифференциальное уравнение первого порядка называется линейным, если его можно записать в виде: y’ + p(x)*y = g(x). Метод интегрирования: 1) метод Бернулли: Решение уравнения ищется в виде произведения двух других функций, т.е. с помощью подстановки y=uv, где u=u(x) и v=v(x). Тогда y’=u’v+uv’. Подставляем в уравнение: u’v+uv’+p(x)uv = g(x) => v’+p(x)v = 0 => dv/v=-p(x)dx => => ln|v| = - => => , U(x) = F(x) + C. Уравнение Бернулли:

37. Уравнение в полных дифференциалах.

Уравнение P(x;y)dx+Q(x;y)dy = 0 называется уравнением в полных дифференциалах, если его левая часть есть полный дифференциал некоторой функции u(x;y), т.е. P(x;y)dx+Q(x;y)dy = du(x;y). ДУ можно записать в виде du(x;y) = 0, а его общий интеграл будет: u(x;y) = c. Требования: Если все сделано верно, то все выражения, содержащие x слева и справа, сократятся, останется выражение, содержащее y: . Таким образом, при решении ДУ вида P(x;y)dx+Q(x;y)dy = 0 сначала проверяем выполнения условия . Затем, используя равенства и , находим функцию u(x;y). Решение записываем в виде u(x;y)=c.

38. Задача Коши для уравнения 1-ого порядка.

Задача отыскания решения ДУ первого порядка, удовлетворяющего заданному начальному условию, называется задачей Коши. Теорема (существования и единственности решения задачи Коши). Если в уравнении y’=f(x;y) функция f(x;y) и ее частная производная непрерывны в некоторой области D, содержащей точку (x₀;y₀), то существует единственное решение этого уравнения, удовлетворяющее начальному условию

39. Ду второго порядка. Свойства решений линейных ду.

ДУ второго порядка в общем случае записывается в виде F(x;y;y’;y’’)=0 или в виде, разрешенном относительно старшей производной: y’’=f(x;y;y’). Решением ДУ называется всякая функция , которая при подстановке в уравнение обращает его в тождество. Общим решением ДУ называется функция , где с1 и с2 – не зависящие от x произвольные постоянные, удовлетворяющие условиям: 1) является решением ДУ для каждого фиксированного значения с1 и с2. 2) Каковы бы ни были начальные условия существуют единственные значения постоянных такие, что функция является решением уравнения и удовлетворяет начальным условиям. ЛОДУ второго порядка: Свойства решений: Теорема. Если функции являются частными решениями уравнения то решением этого уравнения является также функция произвольные постоянные. Теорема (структура общего решения ЛОДУ 2 порядка). Если два частных решения ЛОДУ образуют на интервале (a;b) фундаментальную систему, то общим решением это уравнения является функция произвольные постоянные.

40. Линейная независимость функций. Определитель Вронского.

Теорема. Если дифференцируемые функции линейно зависимы на (a;b), то определитель Вронского на этом интервале тождественно равен нулю. Теорема. Если функции - линейно независимые решения уравнения на (a;b), то определитель Вронского на этом интервале нигде не обращается в нуль.

41.Линейные ДУ 2-го порядка. Характеристическое уравнение. Дано 2ого порядка:y’’+py’+qy=0,где p и q постоянны. Будем искать частные решения уравнения в виде y=e^kx, где k – некоторое число(предложено Л.Эйлером). Дифференцируя эту функцию два раза и подставляя выражения для y,y’,y” в уравнение y’’+py’+qy=0, получаем: k²e^kx+pke^kx+qe^kx=0, т.е. e^kx(k²+pk+q)=0, или k²+pk+q=0(e^kx≠0). Уравнение e^kx(k²+pk+q)=0, или k²+pk+q=0(e^kx≠0). называется характеристическим уравнением ДУ y’’+py’+qy=0(его составления достаточно в уравнении y’’+py’+qy=0 заменить y”,y’ и y соответственно k²,k и 1)

42.Линейные ДУ 2ого порядка. ₁ ≠𝜆 ₂ . Если b²-4ac>0, то 𝜆₁ и 𝜆₂ –действительные не равные друг другу числа( ₁ ≠𝜆 ₂). В этом случае частными решениями будут функции x₁ = , . Они линейно независимы, так как = = Следовательно, общее решение ax”+bx”+cx=0 имеет вид y= .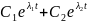

43. Линейные ДУ 2ого порядка. ₁ =𝜆 _2. Если b²-4ac=0, то 𝜆₁ и 𝜆₂ –равные действительные числа ( ₁ =𝜆 ₂). В этом случае пока известно одно частное решение ax”+bx”+cx=0 x₁= , где ₁= 𝜆 ₂ = . Итак, если ₁= 𝜆 ₂ , то общее решение ax”+bx”+cx=0 имеет вид

44. Линейные ДУ 2ого порядка. = если λ₁ и λ₂ – комплексные недействительные числа:

, то общее решение линейных однородных дифференциальных уравнений равно:

45.Неоднородные ДУ 2ого порядка. Структура общего решения. Y”+a₁(x)y’+a₂(x)y=f(x) Общее решение этого уравнения есть сумма y= +y*, где - общее решение соотв.однородного ур-я(без правой части, когда f(x)=0), y* - частное решение уравнения.