
- •15. Несобственные интегралы II рода (интеграл от разрывной функции).
- •16. Определение двойного интеграла.
- •17. Основные свойства, геометрический смысл двойного интеграла.
- •18. Числовые ряды. Основные понятия.
- •19. Необходимый признак сходимости.
- •20. Признаки сравнения знакоположительных рядов.
- •21. Признак Даламбера и радикальный признак Коши.
- •31. Разложение непериодических функций.
- •32. Ряды Тейлора и Маклорена.
- •33. Ду. Основные понятия.
- •34. Уравнения с разделяющимися переменными.
- •35. Однородные ду 1-ого порядка
- •36. Линейные ду первого порядка и уравнение Бернулли.
- •37. Уравнение в полных дифференциалах.
- •38. Задача Коши для уравнения 1-ого порядка.
- •39. Ду второго порядка. Свойства решений линейных ду.
- •40. Линейная независимость функций. Определитель Вронского.
- •46.Метод Лагранжа. Вариации произвольных постоянных.
- •47.Неоднородные ду 2ого порядка с правой частью специального вида.
1.Универсальная
тригонометрическая подстановка.Вычисление
неопределнных интегралов типа
R(sinx,cosx)dx
сводитмя к вычислению интегралов от
рациональной функции подстановкой
tg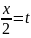 ,
которая называется универсальной.sinx=
,
которая называется универсальной.sinx=
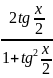 =
=
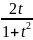 ,
cosx
=
,
cosx
=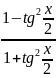 =
=
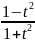 ,
x=2arctgt,
dx=
,
x=2arctgt,
dx=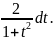 Поэтому R(sinx;cosx)dx
= R(
Поэтому R(sinx;cosx)dx
= R(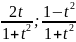 )
)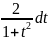 =
R1(t)dt
, где R1(t)
– рациональная функция от t.
Обычно этот способ весьма громоздкий,
зато он всегда приводит к результату.
=
R1(t)dt
, где R1(t)
– рациональная функция от t.
Обычно этот способ весьма громоздкий,
зато он всегда приводит к результату.
2.Интегралы
вида sinnxcosmxdx
( m,n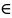 ;m≥0,n≥0
). Для
нахождения таких интегралов используются
следующие приемы: 1.подстановка sinx=t
если n-целое
положительное нечетное число 2.Подстановка
cosx=t
если m-
целое положительное нечетное число 3.
Формулы понижения порядка:cos2x=
;m≥0,n≥0
). Для
нахождения таких интегралов используются
следующие приемы: 1.подстановка sinx=t
если n-целое
положительное нечетное число 2.Подстановка
cosx=t
если m-
целое положительное нечетное число 3.
Формулы понижения порядка:cos2x=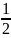 (1+cos2x),
sin2x=
(1-cos2x),
sinxcosx=
sin2x
,если m
и n
- целые неотрицательные четные числа
4. Подстановка tgx=t,
если m+n
– есть четное отрицательное целое
число.
(1+cos2x),
sin2x=
(1-cos2x),
sinxcosx=
sin2x
,если m
и n
- целые неотрицательные четные числа
4. Подстановка tgx=t,
если m+n
– есть четное отрицательное целое
число.
3.Интегралы
вида
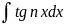 ,
,
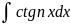 (n
(n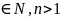 ).
Для
нахождения этих интегралов примен.
ф-лы, с пом. кот. помлед-но понижается
степень m.
tg2x
= (1/cos2x)
- 1, ctg2x
= (1/sin2x)
– 1 1/cosx
= secx,
1/sinx
= cosecx
tg2x
= sec2x
- 1, ctg2x
= cosec2x
– 1 Замечание. Если m-степень частная,
то удобно делать подст. tg x = t., тогда x =
arctg t. dx = dt/ (1+t2) и интеграл сводится к
интегралу от непр. рацион. дроби.
).
Для
нахождения этих интегралов примен.
ф-лы, с пом. кот. помлед-но понижается
степень m.
tg2x
= (1/cos2x)
- 1, ctg2x
= (1/sin2x)
– 1 1/cosx
= secx,
1/sinx
= cosecx
tg2x
= sec2x
- 1, ctg2x
= cosec2x
– 1 Замечание. Если m-степень частная,
то удобно делать подст. tg x = t., тогда x =
arctg t. dx = dt/ (1+t2) и интеграл сводится к
интегралу от непр. рацион. дроби.
4.Интегралы вида sinmxcosnxdx, cosmxcosmxdx, sinmxsinnxdx (m,n ) В этом случае примен. след. тригон. функции: sin mx * cos nx = ½ (sin (m+n) + sin (m-n))
cos mx * cos nx = ½ (cos (m+n) +cos (m-n))
sin mx * sin nx = ½ (cos (m-n) – cos (m+n)) Эти формулы дают нам произведение предс. в виде суммы.
5.
Интегрирование иррациональных функций.
Интегралы
типа
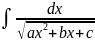 ,
,
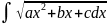 ,
,
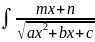 dx
называют неопределенными интегралами
от квалратичных иррациональностей. Их
можно найти следующим образом: под
радикалом выделить полный квадрат и
сделать подстановку x+
dx
называют неопределенными интегралами
от квалратичных иррациональностей. Их
можно найти следующим образом: под
радикалом выделить полный квадрат и
сделать подстановку x+
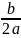 =t.
При этом первые два интеграла приводятся
к табличным, а третий – к сумме двух
табличных интегралов. ТО ЧТО В КОНСПЕКТЕ:
1.
=t.
При этом первые два интеграла приводятся
к табличным, а третий – к сумме двух
табличных интегралов. ТО ЧТО В КОНСПЕКТЕ:
1.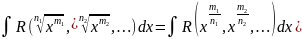 x=ts,
где s
– это общий знаменатель дробей
x=ts,
где s
– это общий знаменатель дробей
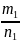 ,
,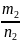 ,…
,…
2.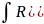 )dx
=
ax+b=ts
,
где s
– это общий знаменатель дробей
,
,…
)dx
=
ax+b=ts
,
где s
– это общий знаменатель дробей
,
,…
3.
,
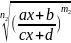 ) dx
=
dx
) dx
=
dx
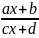 =ts,
где s
– это общий знаменатель дробей
,
,…
=ts,
где s
– это общий знаменатель дробей
,
,…
6.
Интеграл от дифференциального бинома.
Интегралы типа xm(a+bxn)pdx
(называемые интегралами от дифференциального
бинома), где a,b
– действительные числа; m,n,p
– рациональные числа, берутся, как
показал Чебышев П.А., лишь в случае,
когдахотя бы одно из чисел p,
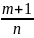 или
+
p
является целым. Рационализация интеграла
в этих случаях осуществляется следующими
подстановками: 1. Если p
– целое число, то подстановка x=tk,
где k
– наименьшее общее кратное знаменателей
дробей m
и n;
2. Если
– целое число, то подстановка a+bxn=ts,
где s
- знаменатель дроби p;
3. Если
+
p
– целое число, то подстановка a+bxn
= xnts,
где s
– знаменатель дроби p.
или
+
p
является целым. Рационализация интеграла
в этих случаях осуществляется следующими
подстановками: 1. Если p
– целое число, то подстановка x=tk,
где k
– наименьшее общее кратное знаменателей
дробей m
и n;
2. Если
– целое число, то подстановка a+bxn=ts,
где s
- знаменатель дроби p;
3. Если
+
p
– целое число, то подстановка a+bxn
= xnts,
где s
– знаменатель дроби p.
7.
Неберущиеся интегралы. В
том случае, когда первообразная некоторой
элементарной функции f(x)
является также элементарной функцией,
говорят, что f(x)dx
«берется», т.е.
интеграл выражается через элементарные
функции(или интеграл вычисляется). Если
же интеграл не выражается через
элементарные функции, то говорят, что
интеграл «не
берется»
(или «его найти нельзя»). Примеры
«неберущихся» интегралов: 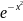 dx
–
интегралл Пуассона(теория вероятностей);
dx
–
интегралл Пуассона(теория вероятностей);
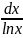 – интегральный логарифм(теория чисел);
cosx2dx,
sinx2dx
–
интегралы Френеля(физика);
– интегральный логарифм(теория чисел);
cosx2dx,
sinx2dx
–
интегралы Френеля(физика); 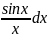 ,
,
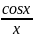 dx
- интегральные
синус и косинус;
dx
- интегральные
синус и косинус; 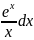 – интегральная
показательная Для любого функция.
– интегральная
показательная Для любого функция.
8.
Определенный интеграл. Определение
Геометрический смысл.
Сумма вида называется интегральной
суммой функции y=f(x)
на отрезке [a;b].
Если интегральная сумма Sn
имеет предел I,который
не зависит ни от способа разбиения
отрезка [a;b]
на частичные отрезки , ни от выбора
точек в них, то число I
называется определенным интегралом
от функции y
= f(x)
на отрезке [a;b]
и обозначается
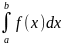 .
Таким
образом,
=
.
Таким
образом,
=
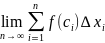 Геом.смысл: Определенный
интеграл от неотрицательной функции
численно равен площади криволинейной
трапеции.
Геом.смысл: Определенный
интеграл от неотрицательной функции
численно равен площади криволинейной
трапеции.
9.
Свойства определенного интеграла 1.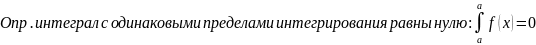 2. Для
любого действительного числа с :
2. Для
любого действительного числа с :
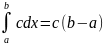 3.
3.
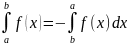 4.
4.
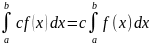
5.
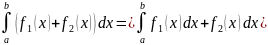 6.Аддитивность:
если есть a<c<b,
то
6.Аддитивность:
если есть a<c<b,
то
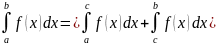 7.
f(x)≥0
→
≥0
8.
Монотонность: f(x)≥g(x)
7.
f(x)≥0
→
≥0
8.
Монотонность: f(x)≥g(x)
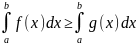 9.
Об оценке определенного интегралы:m
Пусть на интервале [a,b],
ф-ция f(x)
принимает свое наименьшее m
и наибольшее M
значение. m(b-a)≤
9.
Об оценке определенного интегралы:m
Пусть на интервале [a,b],
ф-ция f(x)
принимает свое наименьшее m
и наибольшее M
значение. m(b-a)≤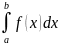 ≤M(b-a)
≤M(b-a)
10.
Теорема о среднем: при f(x)≥0
имеет простой геометрический смысл:
значение определенного интеграла
равно, при некотором площади c
ϵ(a,b)
прямоугольника с высотой f(c)
и основанием.b-a.
Число f(c)=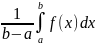 называется средним значением функции
f(x)
на отрезке [a;b].
называется средним значением функции
f(x)
на отрезке [a;b].
10. Определенный интеграл с переменным верхним пределом.
Производная
определенного интеграла по переменному
верхнему пределу равна подынтегральной
функции, в которой переменная
интегрирования заменена этим пределом,
т.е.
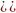 По формуле Ньютона-Лейбница имеем:
По формуле Ньютона-Лейбница имеем:
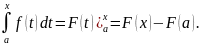 Следовательно,
Это означает, что определенный интеграл
с переменным верхним пределом есть
одна из первообразных подынтегральной
функции.
Следовательно,
Это означает, что определенный интеграл
с переменным верхним пределом есть
одна из первообразных подынтегральной
функции.
11. Формула Ньютона-Лейбница.
Простым
и удобным методом вычисления определенного
интеграла
от непрерывной функции является формула
Ньютона-Лейбница:
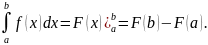 Применяется этот метод во всех случаях,
когда может быть найдена первообразная
функции F(x)
для подынтегральной функции f(x).
Применяется этот метод во всех случаях,
когда может быть найдена первообразная
функции F(x)
для подынтегральной функции f(x).
12. Замена переменной в определенном интеграле.
Пусть
для вычисления интеграла
от непрерывной функции сделана
подстановка x= Теорема: Если: 1) функция x=
Теорема: Если: 1) функция x=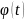 и ее производная x’
=
и ее производная x’
=
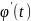 непрерывны при t
€ [α;β]; 2) множеством значений функции
x=
при t
€ [α;β] является отрезок [a;b];
3)
непрерывны при t
€ [α;β]; 2) множеством значений функции
x=
при t
€ [α;β] является отрезок [a;b];
3)
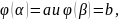 то
то
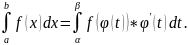 – формула замены переменной в определенном
интеграле.
– формула замены переменной в определенном
интеграле.
13. Интегрирование по частям в определенном интеграле.
Если
функции u
= u(x)
и v
= v(x)
имеют непрерывные производные на
отрезке [a;b],
то имеет место формула
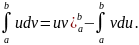 – формула интегрирования по частям
для определенного интеграла.
– формула интегрирования по частям
для определенного интеграла.
14. Несобственные интегралы I рода (интеграл с бесконечным промежутком интегрирования).
Пусть
функция f(x)
непрерывна на промежутке [a;+∞].
Если существует конечный предел
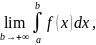 то
его называют несобственным интегралом
первого рода и обозначают
то
его называют несобственным интегралом
первого рода и обозначают
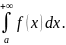 Таким образом,
Таким образом,
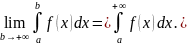 В этом случае говорят, что несобственный
интеграл
В этом случае говорят, что несобственный
интеграл
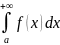 сходится.
Если же указанный предел не существует
или он бесконечен, то говорят, что
интеграл расходится. Аналогично
определяется несобственный интеграл
на промежутке ( -∞;b].
сходится.
Если же указанный предел не существует
или он бесконечен, то говорят, что
интеграл расходится. Аналогично
определяется несобственный интеграл
на промежутке ( -∞;b].
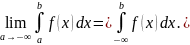 Несобственный интеграл с двумя
бесконечными пределами определяется
формулой:
Несобственный интеграл с двумя
бесконечными пределами определяется
формулой:
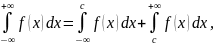 где c
– произвольное число. В этом случае
интеграл слева сходится лишь тогда,
когда сходятся оба интеграла справа.
где c
– произвольное число. В этом случае
интеграл слева сходится лишь тогда,
когда сходятся оба интеграла справа.
15. Несобственные интегралы II рода (интеграл от разрывной функции).
Пусть
функция f(x)
непрерывна на промежутке [a;b]
и имеет бесконечный разрыв при x
= b.
Если существует конечный предел
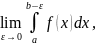 то его называют несобственным интегралом
второго рода и обозначают
.
Таким образом,
то его называют несобственным интегралом
второго рода и обозначают
.
Таким образом,
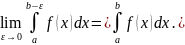 Если предел в правой части существует,
то несобственный интеграл
сходится. Если же предел не существует
или бесконечен, то говорят, что интеграл
расходится. Аналогично, если функция
f(x)
терпит бесконечный разрыв в точке x
= a,
то полагают
Если предел в правой части существует,
то несобственный интеграл
сходится. Если же предел не существует
или бесконечен, то говорят, что интеграл
расходится. Аналогично, если функция
f(x)
терпит бесконечный разрыв в точке x
= a,
то полагают
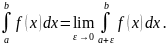 Если функция f(x)
терпит разрыв во внутренней точке c
отрезка [a;b],
то несобственный интеграл второго рода
определяется формулой
Если функция f(x)
терпит разрыв во внутренней точке c
отрезка [a;b],
то несобственный интеграл второго рода
определяется формулой
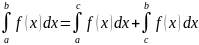 .
В этом случае интеграл слева называется
сходящимся, если оба несобственных
интеграла, стоящих справа, сходятся.
.
В этом случае интеграл слева называется
сходящимся, если оба несобственных
интеграла, стоящих справа, сходятся.
16. Определение двойного интеграла.
Пусть
в замкнутой области D
плоскости Oxy
задана непрерывная функция z=f(x;y).
Разобьем область D
на n
«элементарных областей» Di
, площади которых обозначим через ∆Si
, а диаметры через di.
В каждой области Di
выберем
произвольную точку Mi(xi;yi),
умножим значение f(xi;yi)
функции в этой точке на ∆Si
и
составим сумму всех таких произведений:
f(x1;y1)
*∆S1
+
f(x2;y2)*
∆S2+….+
f(xn;yn)
*∆Sn
=
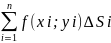 . Эта сумма называется интегральной
суммой функции f(x;y)
в области D.
Рассмотрим предел интегральной суммы,
когда n
стремится к бесконечности таким образом,
что maxdi→0.
Если этот предел существует и не зависит
ни от способа разбиения области D
на части, ни от выбора точек в них, то
он называется двойным интегралом от
функции f(x;y)
по области D
и обозначается
. Эта сумма называется интегральной
суммой функции f(x;y)
в области D.
Рассмотрим предел интегральной суммы,
когда n
стремится к бесконечности таким образом,
что maxdi→0.
Если этот предел существует и не зависит
ни от способа разбиения области D
на части, ни от выбора точек в них, то
он называется двойным интегралом от
функции f(x;y)
по области D
и обозначается
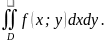 Таким образом:
Таким образом:
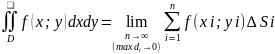 .
.
17. Основные свойства, геометрический смысл двойного интеграла.
1)
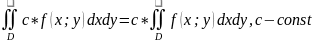 ,
2)
,
2)
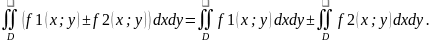 3) Если область D
разбить линией на две области D1
и D2
такие, что D1
3) Если область D
разбить линией на две области D1
и D2
такие, что D1
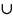 D2
= D,
а пересечение D1
и D2
состоит лишь из линии, их разделяющей,
то:
D2
= D,
а пересечение D1
и D2
состоит лишь из линии, их разделяющей,
то:
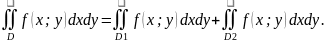 4) Если в области D
имеет место неравенство f(x;y)
≥ 0, то и
4) Если в области D
имеет место неравенство f(x;y)
≥ 0, то и
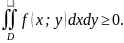 Если в области D
функции f(x;y)
и g(x;y)
удовлетворяют неравенству f(x;y)
≥ g(x;y),
то и
Если в области D
функции f(x;y)
и g(x;y)
удовлетворяют неравенству f(x;y)
≥ g(x;y),
то и
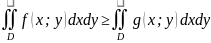 .
5)
.
5)
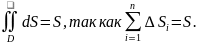 6) Если функция f(x;y)
непрерывна в замкнутой области D,
площадь которой S,
то mS
≤
6) Если функция f(x;y)
непрерывна в замкнутой области D,
площадь которой S,
то mS
≤
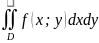 ≤ MS,
где m
и M
– соответственно наименьшее и наибольшее
значения подынтегральной функции в
области D.
7) Если функция f(x;y)
непрерывна в замкнутой области D,
площадь которой S,
то в этой области существует такая
точка (x0;y0),
что
≤ MS,
где m
и M
– соответственно наименьшее и наибольшее
значения подынтегральной функции в
области D.
7) Если функция f(x;y)
непрерывна в замкнутой области D,
площадь которой S,
то в этой области существует такая
точка (x0;y0),
что
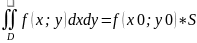 .
Геометрический
смысл:
Величина двойного интеграла от
неотрицательной функции равна объему
цилиндрического тела. (
.
Геометрический
смысл:
Величина двойного интеграла от
неотрицательной функции равна объему
цилиндрического тела. (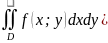
18. Числовые ряды. Основные понятия.
Числовым
рядом называется выражение вида:
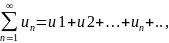 где u1,u2,…,un,…
- действительные или комплексные числа,
называемые членами ряда, un
– общим членом ряда. Ряд считается
заданным, если известен общий член
ряда, выраженный как функция его номера
n:
un
= f(n).
Сумма первых n
членов ряда называется n-ой
частичной суммой ряда и обозначается
через Sn.
Если
существует конечный предел S
=
где u1,u2,…,un,…
- действительные или комплексные числа,
называемые членами ряда, un
– общим членом ряда. Ряд считается
заданным, если известен общий член
ряда, выраженный как функция его номера
n:
un
= f(n).
Сумма первых n
членов ряда называется n-ой
частичной суммой ряда и обозначается
через Sn.
Если
существует конечный предел S
=
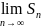 последовательности частичных сумм
ряда, то этот предел называют суммой
ряда и говорят, что ряд сходится.
Записывается:
последовательности частичных сумм
ряда, то этот предел называют суммой
ряда и говорят, что ряд сходится.
Записывается:
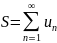 .
Если
не существует или
.
Если
не существует или
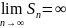 ,
то ряд называют расходящимся. Такой
ряд суммы не имеет. Свойство 1. Если ряд
сходится и его сумма равна S,
то ряд
,
то ряд называют расходящимся. Такой
ряд суммы не имеет. Свойство 1. Если ряд
сходится и его сумма равна S,
то ряд
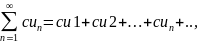 где с – произвольное число, также
сходится и его сумма равна cS.
Если же ряд расходится и с ≠ 0, то и ряд
расходится. Свойство 2. Если сходится
ряд
где с – произвольное число, также
сходится и его сумма равна cS.
Если же ряд расходится и с ≠ 0, то и ряд
расходится. Свойство 2. Если сходится
ряд
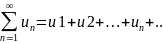 и сходится ряд
и сходится ряд
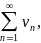 а их суммы равны S1
и S2
соответственно, то сходятся и ряды
а их суммы равны S1
и S2
соответственно, то сходятся и ряды
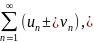 причем сумма каждого равна соответственно
S1
± S2.
Свойство 3. Если к ряду прибавить (или
отбросить) конечное число членов, то
полученный ряд и ряд сходятся или
расходятся одновременно.
причем сумма каждого равна соответственно
S1
± S2.
Свойство 3. Если к ряду прибавить (или
отбросить) конечное число членов, то
полученный ряд и ряд сходятся или
расходятся одновременно.
