
Министерство образования Республики Беларусь Белорусская Государственная политехническая Академия
Кафедра технической физики
МЕТОДИЧЕСКОЕ ПОСОБИЕ
к выполнению лабораторной работы № 111
«Определение отношения теплоемкостей газа методом адиабатического расширения.»
Минск 2000
УДК 539.19 (076.5)
Методическое пособие к выполнению лабораторной работы «Определение отношения теплоемкостей газа методом адиабатического расширения.», Авсиевич О.И., Качан П.Н. - Мн. :2000. -14с.
В методическом пособии изложены необходимые сведения из теории теплопроводности в соответствии с программой курса физики для ВТУЗов. Дано описание теплотехнического стенда, оборудования для определение коэффициента теплопроводности сравнительным методом в условиях стационарного режима и руководство к выполнению лабораторной работы.
Методическое пособие рассчитано на студентов энергетического, машиностроительного и механико-технологического профиля БГПА.
Составители: Авсиевич О.И., Качан П.Н.
Цель работы.
Изучить первое начало термодинамики.
Изучить теорию теплоемкостей.
Изучить адиабатический процесс в газе.
Освоить метод определения отношения теплоемкостей, и получить численное значение этого отношения.
Теоретическая часть.
Описание установки и вывод рабочей формулы.
Приборы и принадлежности
Микроманометр ММН-(5)-1.0
Насос ручной
Труба стеклянная запаянная
Схема установки
К-кран
М-манометр
Н-насос
Б-стеклянный баллон
Теплоемкость идеальных газов.
К идеальным относят газы, у которых потенциальной энергией взаимодействия молекул можно пренебречь в сравнении с кинетической энергией их хаотического движения. Так, газы, составляющие атмосферу, при температурах, близких к обычным комнатным, могут считаться идеальными вплоть до давлений в несколько десятков атмосфер. Состояние этих газов описывается уравнением Менделеева - Клапейрона
![]() , (1)
, (1)
где P-давление, V-объем, m-масса, M-молярная масса данного газа, R-универсальная газовая постоянная, T-термодинамическая температура.
Внутренняя энергия идеального газа U складывается из кинетических энергий хаотического движения молекул.
![]() (2)
(2)
здесь N –число молекул, к - средняя кинетическая энергия одной молекулы.
Молекулярно-кинетическая теория связывает среднюю кинетическую энергию молекулы Е с температурой и числом степеней свободы i соотношением
![]()

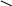

 (3)
(3)
где k - постоянная Больцмана.
Число степеней свободы – это число независимых координат, с помощью которых можно однозначно задать положение частицы в пространстве. Молекулы одноатомных газов могут рассматриваться как точечные объекты. Эти молекулы имеют 3 степени свободы i=3, определяющие их поступательное движение вдоль осей X, Y, Z.
Двухатомная молекула имеет 5 степеней свободы: 3 – поступательного и 2 – вращательного движения. Этими свойствами обладают молекулы N2, O2, H2 при температурах, близких к комнатным. Трех- и более атомная молекула имеет число степеней свободы, зависящие от строения и температуры газа. Жесткая трехатомная молекула CO2 имеет 6 степеней свободы (i=6) при комнатной температуре.
На каждую степень свободы приходится энергия, равная kT/2 – это закон равномерного распределения энергии хаотического движения молекул по степеням свободы.
Полное число молекул газа можно найти по формуле
![]() (4)
(4)
где N0 – число Авогадро, m/M – число молей.
Учтя (3) и (4) и подставив значение их в (2), выразим внутреннюю энергию газа

![]() (5)
(5)
так как N0K=R, выражение (5) примет вид
![]() (6)
(6)
Подставив в (6) значение mRT/M из уравнения Менделеева - Клапейрона, получим
![]() (61)
(61)
Изменение параметров состояния P, V, T называется термодинамическим процессом. Термодинамический процесс может быть описан количественно на основе закона сохранения энергии (первого начала термодинамики)
dQ=dU+dA. (7)
Этот закон можно сформулировать так: Теплота dQ, полученная газом, идет на увеличение внутренней энергии dU и на работу dA, совершенную газом против внешних сил.
Так как работа dA=PdV , где dV – увеличение объема газа, то уравнение первого начала термодинамики можно записать:
dQ=dU+PdV (8)
Теплоту dQ можно выразить через удельную теплоемкость С:
dQ=cmdT (9)
Подставив (9) в (8) и выполнив преобразования, получим формулу для определения удельной теплоемкости идеальных газов:
![]() (10)
(10)
И
 з
(10) следует, что удельная теплоемкость
газа зависит от вида процесса. Выделяют
две теплоемкости: при постоянном объеме
Cv и
при постоянном давлении Cp.
Удельная теплоемкость при постоянном
объеме Cv
определяется из условия V=const.
При этом dA=PdV=0,
и вся теплота dQ, полученная
газом, идет на увеличение его внутренней
энергии dU. Из (6) следует,
что dU=imRdT/2M.
Подставив это значение в (10), после
сокращения получим выражение
з
(10) следует, что удельная теплоемкость
газа зависит от вида процесса. Выделяют
две теплоемкости: при постоянном объеме
Cv и
при постоянном давлении Cp.
Удельная теплоемкость при постоянном
объеме Cv
определяется из условия V=const.
При этом dA=PdV=0,
и вся теплота dQ, полученная
газом, идет на увеличение его внутренней
энергии dU. Из (6) следует,
что dU=imRdT/2M.
Подставив это значение в (10), после
сокращения получим выражение
![]() (11)
(11)
Молярная теплоемкость газа при этих условиях определяется соотношением
![]() (12)
(12)
Удельная теплоемкость газа при постоянном давлении Cp определяется уравнением (10) с учетом (11) и соотношения, полученного из уравнения Менделеева-Клапейрона (1):
![]() (13)
(13)
После сокращений получим выражение:
![]() (14)
(14)
Молярная теплоемкость при постоянном давлении может быть выражена соотношением Cp=cpμ. Следовательно,
![]() (15)
(15)
С учетом (12) данное выражение можно записать:
Cp=Cv+R (16)
Уравнение (16) называется уравнением Майера. Из этого уравнения видно, что Cp больше Cv. Обусловлено это тем, что часть тепла при изобарическом процессе расходуется на работу расширения газа.
Экспериментальные измерения теплоемкостей газов затруднены, так как эти теплоемкости много меньше теплоемкостей сосудов, в которых находятся газы. Сравнительно легко можно найти отношение . Подставив в это отношение значения Cv и Cp из (12) и (15), найдем
![]() (17)
(17)
Зная γ, можно определить строение молекул, число их степеней свободы и вычислить внутреннюю энергию газа. Для определения γ применяют адиабатный процесс.
