
115
.pdfБелорусский Национальный Технический Университет
Кафедра «Техническая физика»
Лаборатория механики и молекулярной физики
Лабораторная работа № 115
Определение коэффициентов вязкости жидкости методом Стокса
Составители: Андрюшкевич А.А., Русакевич Д.А.
Минск 2004
2 |
Определение коэффициентов вязкости жидкости |
1.Цель работы.
1.Ознакомиться с некоторыми особенностями жидкого состояния.
2.Изучить явление внутреннего трения.
3.Определить динамический и кинематический коэффициенты вязкости жидкости методом Стокса.
2.Список литературы.
1.И. В. Савельев. Курс общей физики. М.: «Наука», 1982, том 1.
2.Б. М. Яворский, А. А. Детлаф. Справочникпофизике. М.: «Наука», 1985.
3.И.. И. Н а р к е в и ч, Э. И. В о л м я н с к и й, С. И. Л о б к о. Физика для ВТУЗов. Механика. Молекулярнаяфизика. Мн.: «Вышэйшаяшкола»,1992.
4.Т. А. Зисман, О. М. Тодес. Курсобщейфизики. Киев: «Днiпро»,1994
3.Порядок теоретической подготовки и выполнения работы.
Изучить и законспектировать в тетрадь следующие вопросы:
1.Особенности жидкого состояния.
2.Вязкость (внутреннее трение) в жидкости.
3.Суть метода Стокса по определению коэффициентов вязкости жидкости.
4.Вывод рабочей формулы.
4.Вопросы к зачету.
1.Чем обусловлено внутреннее трение в жидкости?
2.От чего зависит величина силы внутреннего трения в жидкости?
3.Что называется динамическим коэффициентом вязкости, от чего он зависит?
4.В каких единицах измеряются коэффициенты вязкости?
5.В чем состоит метод Стокса определения коэффициента вязкости жидкости?
6.Вывод расчетной формулы.
7.В чем трудность определения коэффициента вязкости непосредственно по формуле Стокса?
8.Почему в работе используются шарики малых размеров? Можно ли использовать для опыта не стальные шарики, а пластмассовые, деревянные и т.д. Ответ обосновать
9.Почему определяется время движения шарика только на некотором участке, а не вдоль всей трубы?
5.Указание по технике безопасности
1.Соблюдать осторожность при работе со стеклянными сосудами.
Лабораторная работа № 115. |
3 |
6. Теоретическая часть.
Жидкости занимают промежуточное положение между газообразным и твердым состояниями. Жидкости, как и твердые тела, относятся к конденсированным средам: их молекулы находятся в непосредственной близости друг к другу. В то же время, плотная упаковка молекул не мешает жидкости принимать любую форму, в какую бы ее не поместили. Как твердое тело, жидкость почти несжимаема и очень прочна на разрыв при всестороннем расширении, но как газ – передает давление по всем направлениям одинаково, без характерной для кристалла анизотропии.
Столь противоречивые свойства жидкости можно объяснить лишь тем, что агрегатное состояние жидкости реализуется в таком температурном интервале, когда энергия теплового движения молекул достаточна для разрушения кристаллической структуры, но еще мала для полного разрыва связей, удерживающих молекулы в пределах конечного объема. Рентгеноструктурные исследования показывают, что в жидкости существует так называемый ближний порядок в расположении молекул и отсутствует дальний.
Средние расстояния r между молекулами в жидкости близки к расстоянию, соответствующему минимальному значению энергии взаимодействия, т.е. равновновесию. Молекулы большую часть времени колеблются около своих положений равновесия. В силу хаотичности теплового движения скорости и амплитуды колебаний соседних молекул различны, и время от времени соседние молекулы перескакивают и «застревают» в новых положениях равновесия и начинают колебаться около них. С ростом температуры растет средняя энергия теплового движения, а с ней и амплитуда колебаний и частота перескоков молекул из одного положения равновесия в соседние.
Наиболее ярким свойством жидкости является ее вязкость. Вязкостью или внутренним трением называется появление сил трения между слоями жидкости или газа, движущимися относительно друг друга параллельно и с разными скоростями.
Причиной вязкости является наложение упорядоченного движения слоев с различными скоростями v и теплового хаотического движения молекул со скоростями, зависящими от температуры.
Предположим, что жидкость течет так, что вектор скорости течения vr имеет постоянное направление, а величина скорости v меняется только вдоль одного направления, перпендикулярного направлению вектора скорости. Выберем его в качестве оси X, тогда скорость будет являться функцией x, т.е. v=f(x)
Для характеристики быстроты изменения v в направлении x вводится понятие
V
dS |
|
|
I |
II |
|
Vr(x) |
|
|
Рисунок 1 |
X |
|
|
||
градиента скорости dvdx в направлении оси x.
Между поверхностью твердого тела и всякой реальной жидкостью существуют силы молекулярного сцепления, приводящие к тому что непосредственно прилегающий к стенке слой полностью «прилипает» к ней, т.е. скорость пристеночного слоя равна нулю. Так как молекулы жидкости большую часть времени находятся около положения равновесия, то движущаяся масса жидкости увлекает соседние слои в основном за счет сил сцепления и в меньшей степени за счет

4 |
Определение коэффициентов вязкости жидкости |
перехода молекул из одного слоя в другой. По мере удаления от стенки скорость слоев увеличивается и возникает поток импульса по направлению от жидкости к стенке. Импульс dP, переносимый за время dt через площадку dS, расположенную параллельно вектору скорости, выражается формулой:
dP = −η dvdx dSdt .
С другой стороны, по второму закону Ньютона F = dPdt , поэтому
F = −η dvdx dS
Сила Fr называется силой внутреннего трения.
Коэффициент η называется динамическим коэффициентом вязкости или
коэффициентом внутреннего трения. Динамический коэффициент численно равен силе внутреннего трения, действующей на единицу поверхности взаимодействующих слоев при градиенте скорости, равном единице.
В СИ единицей измерения динамического коэффициента вязкости является
1Па с = Нм2с = мкгс .
Динамический коэффициент вязкости, зависящий от плотности среды, определяет быстроту передачи импульса от слоя к слою. Быстрота выравнивания скорости потока определяется
величиной ν = ηρ , называемой кинематической вязкостью, которая не зависит от плотности
жидкости. Единицей измерения ν в системе СИ является 1 м2/с.
При нагревании жидкость «разрыхляется» за счет увеличения амплитуды колебаний и частоты перехода молекул из одного положения равновесия в другое.
Коэффициент внутреннего трения жидкости зависит от температуры жидкости
W
η = Aρe kT ,
где A- коэффициент, зависящий от рода жидкости, ρ - плотность жидкости,
k - постоянная Больцмана,
W - энергия вязкостной активации – энергия, которую нужно сообщить молекуле, чтобы она могла перескочить из одного положения равновесия в соседнее.
С ростом температуры вязкость жидкости быстро падает. При понижении температуры вязкость большинства жидкостей быстро возрастает. Примером исключения является гелий. При приближении к абсолютному нулю температуры гелий не только не

Лабораторная работа № 115. |
|
|
|
5 |
увеличивает своей вязкости, но и переходит в «сверхтекучее» состояние, характеризуемое |
||||
полным отсутствием вязкости. |
|
|
|
|
|
|
7. |
Вывод рабочей формулы. |
|
r |
|
Метод основан на исследовании движения |
||
FC |
шарика в вязкой смачивающей жидкости. На |
|||
r |
падающий в жидкости шарик действуют силы (рис.2): |
|||
FA |
|
|
|
|
l |
1. |
Сила тяжести |
|
|
mgr |
|
P = mg = 4 πr3 ρш g |
|
|
|
|
, (7-1) |
||
|
|
|
3 |
|
Y |
где |
ρш - плотность материала шарика, g- ускорение |
||
Рисунок 2 |
свободного падения, r- радиус шарика. |
|||
|
|
|
|
|
2.Выталкивающая сила (Архимеда):
FA = |
4 |
πr3 ρж g , |
(7-2) |
|
3 |
||||
|
|
|
где ρж -плотность жидкости.
3.Сила сопротивления среды, обусловленная вязкостью, определяемая по формуле Стокса
F = 6πηrv , |
(7-3) |
где η - динамический коэффициент вязкости, v- скорость движения шарика.
Согласно II закону Ньютона:
FrA + FrC + mgr = mar |
(7-4) |
Проецируя на ось Y, получим:
|
mg-FA-FC=ma |
(7-5) |
|
4 |
πr 3 (ρш − ρж )g − 6πηrv = ma |
.(7-6) |
|
3 |
|||
|
|
В начале движения, пока скорость падающего шарика мала, он движется ускоренно. Довольно быстро, уже через несколько сантиметров от начала движения, скорость достигнет такого значения v0, при котором равнодействующая этих сил обратится в нуль и движения станет равномерным. Тогда:
4 |
πr3 (ρ |
ш |
− ρ |
ж |
)g = 6πηrv |
.(7-7) |
|
||||||
3 |
|
|
0 |
|
||
|
|
|
|
|
|
6 |
|
|
Определение коэффициентов вязкости жидкости |
||
|
Определив опытным путем скорость v0 = |
l |
, где l- расстояние между двумя метками, |
||
|
t |
||||
|
|
|
|
|
|
|
пройденное шариками за время t. Зная ρж и ρш , можно определить η : |
||||
|
η = |
2r 2 |
(ρш − ρж )gt |
.(7-8) |
|
|
|
9l |
|||
|
|
|
|
||
Так как на опыте удобнее определять не радиус r , а диаметр шарика D=2r, то формула принимает окончательный вид:
η = |
D2 |
(ρш |
− ρж )gt |
.(7-9) |
|
18l |
|||
|
|
|
||
Это равенство справедливо лишь в том случае, когда шарик падает в безграничной среде. Если же он падает вдоль оси трубки радиуса R, то приходится учитывать влияние боковых стенок. Поправки в формуле Стокса в таком случае обосновал Ладенбург. С учетом этих поправок (7-9) принимает вид:
η = |
D2 |
(ρш − ρж )gt |
.(7-10) |
|||
18l(1+ 2.4 |
r |
) |
||||
|
|
|||||
|
R |
|
||||
|
|
|
|
|
||
Если в опыте r<<R, то можно пользоваться формулой (7-9).
8.Описание установки.
8.1.Приборы и принадлежности :
1.сосуд с исследуемой жидкостью;
2.стальные шарики;
3.штангенциркуль;
4.линейка;
5.пинцет
9.Порядок проведения эксперимента (для Лаборатории № 315).
1. При помощи миллиметровой линейки измерить расстояние между метками на цилиндре с исследуемой жидкостью.
2.Измерить диаметр шарика.
3.При помощи пинцета осторожно опустить шарик в жидкость как можно ближе к оси цилиндра.
4.Измерить время t прохождения шариком расстояния между метками.
5.Опыт повторить 3-5 раз с различными шариками.
6.Результаты всех измерений занести в таблицу.
Лабораторная работа № 115. |
|
|
|
|
|
7 |
||||
|
|
|
|
|
|
|
Таблица 1 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
№ |
l |
D |
∆D |
t |
∆t |
η |
ν |
||
|
(м) |
(м) |
(м) |
(c) |
(c) |
(Па*с) |
(м2/с) |
|
|
|
|
|
|
||||||||
|
1 |
|
|
|
|
|
- |
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
- |
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
- |
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ср. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7.Согласно данным полученным в таблице 1 , используя формулы ( 10-2 ) и (10-3) рассчитать значения динамической вязкости и кинематической вязкости
8.Выведя формулы для учета погрешности ( 10-4)-(10-7), рассчитать погрешностиεη , ∆η,εν , ∆ν
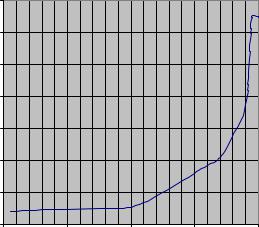
9.Используя график зависимости вязкости водного раствора от процентного содержания в нем воды определить содержание воды в исследуемом растворе.
|
Вязкость водного раствора глицерина |
||||
|
1 ,4 |
|
|
|
|
|
1 ,2 |
|
|
|
|
ть , |
1 |
|
|
|
|
0 ,8 |
|
|
|
|
|
зк о с |
|
|
|
|
|
0 ,6 |
|
|
|
|
|
В я |
0 ,4 |
|
|
|
|
|
|
|
|
|
|
|
0 ,2 |
|
|
|
|
|
0 |
|
|
|
|
|
6 0 |
7 0 |
8 0 |
9 0 |
1 00 |
|
|
Содержание глицерина, % |
|
||
10. Окончательный результат записать в виде:
η = (η ± ∆η)Па с |
ν = (ν ±∆ν )м2 / с |
Содержание воды в глицерине …%

8 |
Определение коэффициентов вязкости жидкости |
|
10. Структура и содержание отчета. |
1) Цель работы.
2)Приборы и принадлежности.
3)Схема установки (см. рисунок 2).
4)Физическая модель:
Вкачестве физической модели принято:
1. жидкость в сосуде вязкая, несжимаемая;
2.размеры и масса шарика и размер сосуда подбираются так, что жидкость можно считать простирающейся безгранично;
3.вязкость не зависит от температуры;
4.установившееся движение шарика в жидкости считать равномерным;
5.жидкость смачивающая.
5)Математическая модель:
Вкачестве математической модели принято выражение:
FrC + FrA + mgr = 0 |
(10-1) |
Формула для расчета динамической вязкости исследуемой жидкости:
η = |
D2 |
(ρш |
− ρж )gt |
(10-2) |
|
18l |
|||
|
|
|
||
Формула для расчета кинематической вязкости исследуемой жидкости:
ν = η ρж
Формулы для расчета погрешностей динамической вязкости
εη = |
∆η |
= 2 |
∆D |
+ |
∆g |
+ |
∆t |
+ |
∆l |
+ |
∆ρ |
ш + ∆ρ |
ж |
η |
D |
g |
t |
l |
ρш − ρж |
|
|||||||
|
|
|
|
|
|
|
|||||||
∆η = εηη
Формулы для расчета погрешностей кинематической вязкости
εν = ∆ν = ∆η + ∆ρж ν η ρж
∆ν = ενν
6) Результаты измерений.
Заполнить таблицу в соответствии с указаниями.
7) Результаты расчетов.
(10-3)
(10-4)
(10-5)
(10-6)
(10-7)
Для расчета необходимо взять: ρш = 7800 кг м3 , ρж = 1250 кг м3 ,
∆ρш = ∆ρж = 5 кг м3 , ∆l = 1 10−3 м, ∆g = 0,05 мс2 , D, ∆D,t, ∆t - из таблицы 1.
Лабораторная работа № 115. |
9 |
Порядок выполнения л/р №115 (ауд. 316)
“Определение коэффициентов вязкости жидкости методом Стокса”.
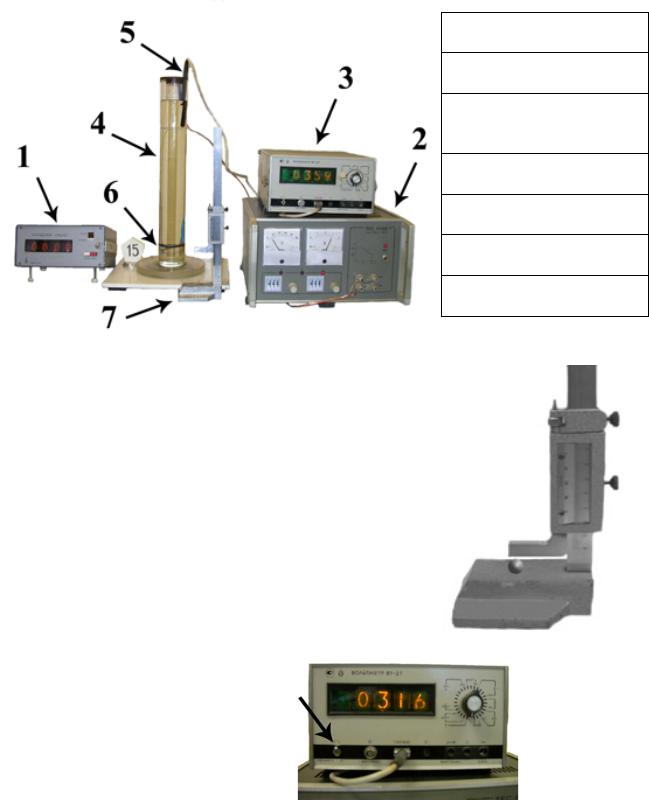
Общий вид установки
1. Измеритель времени (секундомер)
2. Источник нагревательного элемента
3. Вольтметр В7-27 (работ. в режиме
термометра)
4. Стеклянный сосуд
5. Датчик термометра
6. Элемент нагрева
7. Штангенциркуль
1. Подготовьте Таблицу 1
2.Измерьте диаметр шарика (D1) с помощью штангенциркуля, так как форма шарика не является идеально сферической,
необходимо произвести измерение еще дважды (D2, D3), всякий раз поворачивая шарик.
Данные запишите в таблицу 1
3. Включите термометр: (Вольтметр В7-27)

10 |
Определение коэффициентов вязкости жидкости |
4.Запишите в таблицу температуру жидкости.
5.Осторожно поднесите шарик к отверстию в крышке сосуда,
иотпустите.
6. Включите секундомер.
7. В момент, когда шарик будет на уровне верхней метки,
запустите секундомер, нажав кнопку «Отсчет», и удерживайте её.
