31. Разложение непериодических функций.

Непериодическая функция f(x) может быть представлена в виде ряда Фурье на любом конечном промежутке [a;b], на котором она удовлетворяет условиям Дирихле. Для этого можно поместить начало координат в середину отрезка [a;b] и построить функцию f₁(x) периода T=2l=|b-a| такую, что f1(x)=f(x) при –l ≤ x ≤ l. Пусть теперь непериодическую функцию f(x) требуется разложить в ряд Фурье на отрезке [0;l]. Такую функцию можно произвольным образом доопределить на отрезке [-l;0], а затем осуществить ее периодическое продолжение с периодом T=2l. Разложив в ряд Фурье на отрезке [-l;l] полученную таким образом периодическую функцию f₁(x), получим искомый ряд для функции f(x) при x € [0;l]. В частности, функцию f(x) можно доопределить на отрезке [-l;0] четным образом (т.е. чтобы при –l ≤ x ≤ 0 было f(x)=f(-x)). В этом случае функция f(x) разлагается в ряд Фурье, который содержит только косинусы. Если же функцию продолжить на отрезок [-l;0] нечетным образом, то она разлагается в ряд, состоящий только из синусов.

32. Ряды Тейлора и Маклорена.

Если функция f(x) имеет производные любых порядков (т.е. бесконечно дифференцируема) в окрестности точки x₀ и остаточный член R_n(x) стремится к нулю при n→ ∞ ( ), то из формулы Тейлора получается разложение функции f(x) по степеням (x-x₀), называемое рядом Тейлора: 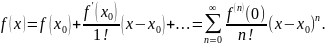Если в ряде Тейлора x₀ = 0, то получим разложение функции по степеням x в так называемый ряд Маклорена: 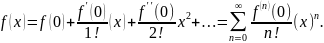Для того, чтобы ряд Тейлора сходился именно к той функции, для которой он записан, необходимо и достаточно, чтобы: 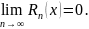Теорема. Если в интервале сходимости от –R до R, любая производная ограничена одной и той же константой M, то f(x) разлагается в ряд Тейлора.

33. Ду. Основные понятия.

Уравнения, связывающие независимую переменную, искомую функцию и ее производные, называются дифференциальными. Решением дифференциального уравнения называется функция, которая при подстановке в уравнение обращает его в тождество. Так, решением уравнения y’ = f(x) является функция y = F(X0) – первообразная для функции f(x). Если искомая функция зависит от одной переменной, то ДУ называют обыкновенным; в противном случае – ДУ в частных производных. Наивысший порядок производной, входящей в ДУ, называется порядком этого уравнения. Процесс отыскания решения ДУ называется его интегрированием, а график решения ДУ – интегральной кривой.

34. Уравнения с разделяющимися переменными.

Уравнения с разделяющимися переменными имеют вид: 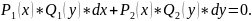Это уравнение легко сводится к уравнению путем почленного деления его на Q₁(y)*P₂(x)≠0. Получаем: 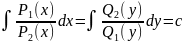- общий интеграл.

35. Однородные ду 1-ого порядка

Функция f(x) называется однородной функцией n-ого порядка, если при умножении каждого ее аргумента на произвольный множитель λ вся функция умножается на λⁿ, т.е. f(λx;λy)= λⁿf(x;y). Дифференциальное уравнение y’=f(x;y) называется однородным, если функция f(x;y) есть однородная функция нулевого порядка. Однородное уравнение можно записать в виде: 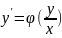. Однородное уравнение преобразуется в уравнение с разделяющимися переменными при помощи замены переменной (подстановки) . 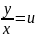Найдя его общее решение, следует заменить в нем u на y/x. Получим общее решение (интеграл) исходного уравнения.