
- •1.Двумерные алгоритмы. Преобразование координат: сдвиг, поворот.
- •2.Двумерные алгоритмы. Окна и Области вывода. Отсечение линий (общее представление, простой алгоритм). Автоматический подбор размеров и позиций.
- •3.Двумерные алгоритмы Понятие о рекурсии. Понятие о фракталах. Сглаживание кривых.
- •4.Векторы. Скалярное и векторное произведения векторов.
- •5.Однородные координаты.
- •6.Перенос и повороты в трехмерном пространстве.
- •7.Видовое преобразование
- •8.Перспективное преобразование
- •9.Алгоритм определения невидимых линий.
- •10.Удаление невидимых линий и поверхностей. Алгоритмы плавающего горизонта и Робертса.
- •11.Алгоритм Варнока.
- •12.Алгоритмы построения криволинейных поверхностей.
- •13. Типы графических устройств: графические дисплеи на запоминающей трубке, векторные графические дисплеи с регенерацией изображения, растровые графические дисплеи с регенерацией изображения.
- •14. Устройство электронно-лучевой трубки, устройство цветной растровой элт.
- •16.Алгоритм брезенхема для генерации окружности
- •17.Заполнение многоугольников
- •19. Построение реалистических изображений. Простая модель освещенности. Определение нормали к поверхности. Определение вектора отражения.
- •20. Построение реалистических изображений. Закраска методами Гуро и Фонга.
- •22.Тени.
4.Векторы. Скалярное и векторное произведения векторов.
Скалярное произведение двух векторов a и b определяется как
a·b=|a|* |b|* cos γ если a≠0 и b≠0
a·b=0 если a=0 или b=0
где γ угол между a и b
Применяя это правило к единичным векторам i, j, kнаходим
i·i = j·j =k·k = 1
i·j =j·i = i·k = k·i =j·k=k·j = 0
Приравнивая a=b,
получаем a·a = |a|^2 ,так что |a|=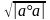
Важные свойства скалярного произведения:
1)c(ku·v) =ck(u·v)
2)(cu + kv) · w = cu·w + kv·w
3)u·v = v·u
4)u·u = 0 только если u = 0
Скалярное произведение векторов u = [u1 u2 u3 ] v = [v1 v2 v3] может быть вычислено как
u·v=u1v1 + u2v2 + u3v3
Векторное произведение двух векторов а и b обозначается
a
 b
b
и равно вектору v, который обладает дующими свойствами.
Если а = сb для некоторого скаляра с, то v=0. В противном случае длина вектора v равна
| v | = |a| |b| sin γ
где γ – угол между векторами а и b, а направление вектора v перпендикулярно обоим векторам а и b и таково, что a, b, v именно в таком порядке образуют правостороннюю тройку. Последнее означает, что, если вектор а поворачивается на угол γ < 180 в направлении к вектору b, то вектор v имеет направление перемещения винта с правой резьбой, поворачиваемого в том же направлении. Из этого определения можно вывести следующие свойства векторного произведения
(k*a) b = k*(a b) для любого вещественного числа k;
a (b + c) = a b + a c
a b = -b a
В общем случае a (b c) (a b) c.
Используя правую ортогональную систему координат с единичными векторами i, j, kб будем иметь
i i = j j = k k =0
i j=k, j i=i; k 1 = j; j i=-k; k*j=-i; i k=-j;
Используя эти значения векторных произведений в расширенной записи векторного произведения
a b = (a1i + a2j + a3k) (b1i + b2j + b3k)
получим
a b = (a2 b3 – a3 b2) i + (a3 b1 – a1 b3) j
что может быть записано в виде
a
b = i +
i +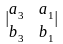 j +
j +
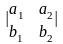 k
k
или в форме более удобной для запоминания
a
b =
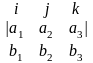
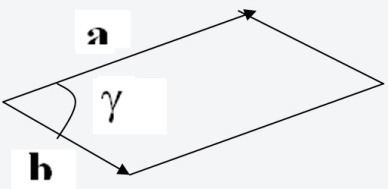
Если через векторы а и b обозначены соседние стороны параллелограмма, то площадь этого параллелограмма равна длине вектора a b
Смешанное и векторное произведения векторов в координатной форме.
Теорема. Пусть ![]() ,
, ![]() ,
, ![]() .
Тогда:
.
Тогда:
1)![]()
![]()
2) 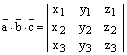
Векторное произведение часто записывают в форме определителя:
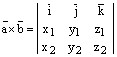 .
.
Разумеется это не определитель, а лишь форма записи векторного произведения. Она компактна и удобна для запоминания.
Следствие. Определитель не изменяется при круговой перестановке строк (столбцов) определителя. При транспозиции двух строк (столбцов) определитель меняет знак.
5.Однородные координаты.
Запись [x y 1] для обозначения матрицы, состоящей только из одной строки, называется вектором-строкой. Такая запись может рассматриваться как частный случай записи [x y w], где числа x, y, w называются однородными координатами. Эти три числа однородных координат применяются для обозначения точки в двумерном пространстве.

На рисунке имеем ось х и ось w, так что точка задается парой координат (x,w). Любая точка Р (x,y), не лежащая на оси х, имеет свою центральную проекцию Р’(X,1), определяемую как точка пересечения прямой линии ОР с прямой линией l, описываемой уравнением w=1.Точка начала координат является центром проекции. Отрезок прямой линии РО может рассматриваться как луч света из объекта Р в глаз, расположенный в точке О. Для точек Q(0, w) и Q’(0,1) получим два подобных треугольника OPQ и OP’Q’, так что
![]()
Х=
Все точки (x,w) со свойством x=wX лежат на линии ОР и имеют одну и ту же проекцию P’ Если интересоваться только проекциями на прямую линию l, а не фактическими значениями x и w, то имеет значение только их отношение. Вполне естественно учитывать только одну координату Х вместо пары (Х, 1), если учитывать только точки на прямой l. Если же все-таки требуется использовать координатную пару, то подойдет любая пара чисел (x,w), удовлетворяющая условию x/w=X. В геометрическом смысле координатная пара (wX, w) любой точки Р, отличной от О, на прямой ОР’ может служить обозначением точки P'. Это и реализуется в случае применения однородных координат.
