5.4.МетодМонте-Карло(методстатистическихиспытаний).

Данныйметодродилсяв1949годублагодаряусилиямамериканскихученыхДж.НейманаиСтиваУланавгородеМонте-Карло(княжествоМонако).

МетодМонте-Карло–численныйметодрешенияматематическихзадачприпомощимоделированияслучайныхчисел.

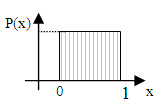
Сутьметодасостоитвтом,чтопосредствамспециальнойпрограммынаЭВМвырабатываетсяпоследовательностьпсевдослучайныхчиселсравномернымзакономраспределенияот0до1.Затемданныечисласпомощьюспециальныхпрограммпреобразуютсявчисла,распределенныепозаконуЭрланга,Пуассона,Релеяит.д.

Полученныетакимобразомслучайныечислаиспользуютсявкачествевходныхпараметровэкономическихсистем:

Примногократноммоделированиислучайныхчисел,которыемыиспользуемвкачествевходныхпараметровсистемы(модели),определяемматематическоеожиданиефункцииM(Q)и,придостижениисреднимзначениемфункцииQуравненияненижезаданного,прекращаеммоделирование.

Статистическиеиспытания(методМонте-Карло)характеризуютсяосновнымипараметрами:

D-заданнаяточностьмоделирования;

P–вероятностьдостижениязаданнойточности;

N–количествонеобходимыхиспытанийдляполучениязаданнойточностисзаданнойвероятностью.

ОпределимнеобходимоечислореализацийN,тогда

(1-D)будетвероятностьтого,чтоприодномиспытаниирезультатнедостигаетзаданнойточностиD;

(1-D)N–вероятностьтого,чтоприNиспытанияхмынеполучимзаданнойточностиD.

ТогдавероятностьполучениязаданнойточностиприNиспытанияхможнонайтипоформуле

(19)

Формула(19)позволяетопределитьзаданноечислоиспытанийдлядостижениязаданнойточностиDсзаданнойвероятностьюР.

D	ЗначениеР
	0,80	0,20	0,95	0,99
0,100,050,0250,01250,006	16 32 64 161 322	22 45 91 230 460	29 59 116 299 598	44 90 182 459 919

СлучайныечислаполучаютсявЭВМспомощьюспециальныхматематическихпрограммилиспомощьюфизическихдатчиков.ОднимизпринциповполученияслучайныхчиселявляетсяалгоритмНеймана,когдаизодногослучайногочислапоследовательновыбираетсясерединаквадрата

g₀=0,9876g₀²=0,97531376

g₁=0,5313g₁²=0,28654609

g₂=0,6546g₂²=0,42850116ит.д.

Крометогоданныечислапроверяютсянаслучайностьиполученныечислазаносятсявбазуданных.

Физическиедатчикиразрабатываютсянаэлектронныхсхемахипредставляютсобойгенераторыбелого(нормального)шума,тоестькогдавспектральномсоставешумаимеютсягармоничныесоставляющиесчастотойF®¥.Изданногобелогошумаметодомпреобразованияполучаютсяслучайныечисла.

32.МетодМаксимальногоправдоподобия.

Методмаксимальногоправдоподобия

Оценкоймаксимальногоправдоподобиянеизвестногопараметрапогруппированнымнаблюдениямназываетсятакоезначениепараметра,прикоторомфункцияправдоподобия

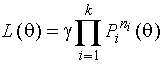,(1.2.1)

где -некотораяконстантаи -вероятностьпопаданияна­­блю­денияв -ыйинтервалзначений,достигаетмаксимуманамножествевозможныхзна­ченийпараметра.Здесьпредполагается,чтодлявсех .ДлявычисленияОМПдифференцируютфунк­циюправдоподобияпо и,приравниваяпроизводныенулю,получаютсистемууравненийправдоподобия

,

где -размерностьвекторапараметров .

Функцияправдоподобиядлячастичногруппированнойвыборкиимеетвид

,

системауравненийправдоподобия

,

где -функцияплотностислучайнойвеличины,(1)и(2)означают,чтосуммированиеиумножениеосуществляютсяпоинтерваламсгруппированнымиинегруппированнымиданнымисоответственно.

Вслучаедостаточнобольших приопределенныхусловияхрегулярностидляфункцииплотностиОМПсуществуетпрактическивсегда,состоятельнаиасимптотическиэффективна.Условиясуществования,асимптотическойэффек­тив­ностиисостоятельностипогруппированнымицензурированнымвыборкамрассматривалисьвработахГ.КуллдорфаиН.А.Бодина.Г.Г.ЗачепойбылиполученыусловиясуществованияОМПосновныхпараметровраспределенияВейбуллаигамма-рас­пре­де­ления.Внашихработахполученыусловиясущест­вованияиединственностиОМПдляпараметровряданепрерывныхзаконовраспределенияслучайныхвеличин.

Вообщеговоря,методмаксимальногоправдоподобиятребуетзначительногообъемавычислений.Авслучаегруппированныхиличастичногруппированныхданныхвозникаетнеобходимостьврешениизадаччисленногоинтегрирования,втомчисле,ивычислениянесобственныхинтегралов.Именнотрудностивычисли­тельногохарактера,особенновситуациигруппированныхичастичногруппиро­ванныхданных,ограничивалииспользованиеметодамаксимальногоправдоподобия.

Существуетбольшоечислоработ,вкоторыхрассматриваетсявычислениеприближенныхоценокмаксимальногоправдоподобия.Вэтомслучаеисходнаягруппированнаявыборказаменяетсянегруппированной,вкоторойиндивидуальнымзначениямприсваиваютсязначенияцентровинтерваловгруппированияприихравнойдлине.Далеевычисляютсяоценки,азатемвыводятсявыражениядляпоправоккполученнымоценкам.

Описанныевданномразделеметодывычисленияоценокпараметровраспределенийдалеконепредставляютсобойполныйпереченьвсехвозможныхметодов,даэтацельинепреследовалась.

33.Методнаименьшихквадратов.

Методнаименьшихквадратов(МНК,OLS,OrdinaryLeastSquares)—одинизбазовыхметодоврегрессионногоанализадляоценкинеизвестныхпараметроврегрессионныхмоделейповыборочнымданным.Методоснованнаминимизациисуммыквадратовостатковрегрессии.

Необходимоотметить,чтособственнометодомнаименьшихквадратовможноназватьметодрешениязадачивлюбойобласти,еслирешениезаключаетсяилиудовлетворяетнекоторомукритериюминимизациисуммыквадратовнекоторыхфункцийотискомыхпеременных.Поэтомуметоднаименьшихквадратовможетприменятьсятакжедляприближённогопредставления(аппроксимации)заданнойфункциидругими(болеепростыми)функциями,принахождениисовокупностивеличин,удовлетворяющихуравнениямилиограничениям,количествокоторыхпревышаетколичествоэтихвеличинит.д.

Сутьметоданаименьшихквадратов(МНК). Задачазаключаетсявнахождениикоэффициентовлинейнойзависимости,прикоторыхфункциядвухпеременныхаиb принимаетнаименьшеезначение.Тоесть,приданныхаиbсуммаквадратовотклоненийэкспериментальныхданныхотнайденнойпрямойбудетнаименьшей.Вэтомвсясутьметоданаименьшихквадратов. Такимобразом,решениепримерасводитсякнахождениюэкстремумафункциидвухпеременных. Выводформулдлянахождениякоэффициентов. Составляетсяирешаетсясистемаиздвухуравненийсдвумянеизвестными.Находимчастныепроизводныефункции попеременнымаиb,приравниваемэтипроизводныекнулю. Решаемполученнуюсистемууравненийлюбымметодом(напримерметодомподстановкиилиметодомКрамера)иполучаемформулыдлянахождениякоэффициентовпометодунаименьшихквадратов(МНК). Приданныхаиbфункция принимаетнаименьшеезначение.Доказательствоэтогофактаприведенонижепотекстувконцестраницы. Вотивесьметоднаименьшихквадратов.Формуладлянахожденияпараметраaсодержитсуммы , , , ипараметрn-количествоэкспериментальныхданных.Значенияэтихсуммрекомендуемвычислятьотдельно.Коэффициентbнаходитсяпослевычисленияa.

34.ДвухшаговыйМ.Н.К.

Двухшаговыйметоднаименьшихквадратов(ДМНК)используетследующуюцентральнуюидею:наосновеприведеннойформымоделиполучаютдлясверхидентифицируемогоуравнениятеоретическиезначенияэндогенныхпеременных,содержащихсявправойчастиуравнения.ЗатемониподставляютсявместофактическихзначенийиприменяютобычныйМНКкструктурнойформесверхидентифицируемогоуравнения.Всвоюочередь,сверхидентифицируемаяструктурнаямодельможетбытьдвухтипов:либовсеуравнениясистемысверхидентифицируемы,либожесистемасодержитнарядусосверхидентифицируемымииточноидентифицируемыеуравнения.Впервомслучае,есливсеуравнениясистемысверхидентифицируемые,дляоценкиструктурныхкоэффициентовкаждогоуравненияиспользуетсяДМНК.Есливсистемеестьточноидентифицируемыеуравнения,тоструктурныекоэффициентыпонимнаходятсяизсистемыприведенныхуравнений.

Структурнаямодель—этосистемасовместныхуравнений,каждоеизкоторыхнужнопроверятьнаидентификацию.Всямодельсчитаетсяидентифицируемой,еслиидентифицируемокаждоеуравнениесистемы.Еслинеидентифицируемохотябыодноизуравненийсистемы,товсясистеманеидентифицируема.Сверхидентифицируемаямодельдолжнасодержатьхотябыодносверхидентифицируемоеуравнение.Чтобыуравнениебылоидентифицируемо,необходимо,чтобычислопредопределенныхпеременных,отсутствующихвданномуравнении,ноприсутствующихвовсейсистемевцелом,равнялосьчислуэндогенныхпеременныхвданномуравнениибезодного.

Необходимоеусловиеидентификации—этовыполнениесчетногоправила.Есличислопредопределенныхпеременных,отсутствующихвуравнении,ноприсутствующихвсистеме,увеличенноенаединицу,равночислуэндогенныхпеременныхвуравнении,тоуравнениеидентифицируемо.Еслименьше—неидентифицируемо,еслибольше—сверхидентифицируемо.

Этопростоеусловиеявляетсявсеголишьнеобходимым.Ононедостаточно.Достаточнымявляетсяболеесложноеусловиеидентификации,котороенакладываетопределенныеусловиянакоэффициентыматрицпараметровструктурноймодели.Уравнениеидентифицируемо,еслиопределительматрицы,составленнойизкоэффициентовприпеременных,которыеотсутствуютвисследуемомуравнении,ноналичествуютвдругихуравненияхсистемы,неравеннулюиприэтомрангэтойматрицынеменеечислаэндогенныхпеременныхсистемыбезединицы.

Помимоуравнений,параметрыкоторыхнеобходимооценить,вэконометрическихмоделяхиспользуютибалансовыетождествапеременных,коэффициентыприкоторыхравныпомодулюединице.Понятно,чтосамотождествоненужнопроверятьнаидентификацию,т.к.коэффициентывтождествеизвестны.Новпроверкесамихструктурныхуравненийсистемытождестваучаствуют.Наконец,ограничениямогутнакладыватьсятакженадисперсиииковариацииостаточныхвеличин

Алгоритмдвухшаговогометоданаименьшихквадратовреализуетсявчетыреэтапа:

1)наосновеструктурнойформысистемыодновременныхуравненийсоставляетсяеёприведённаяформа;

2)оценкинеизвестныхкоэффициентовприведённойформысистемыодновременныхуравненийрассчитываютсяспомощьютрадиционногометоданаименьшихквадратов;

3)рассчитываютсязначенияэндогенныхпеременных,выступающихвкачествефакторныхвсверхидентифицированномуравнении;

4)всеструктурныекоэффициентыуравненийсистемырассчитываютсятрадиционнымметодомнаименьшихквадратовчерезпредопределённыепеременные,входящиевэтоуравнениевкачествефакторов,изначенияэндогенныхпеременных,полученныхнапредыдущемшаге.

Каквидноизописанияданногоалгоритма,традиционныйметоднаименьшихквадратовприменяетсядвараза(дляопределенияоценокэндогенныхпеременныхприведённойформыидляопределенияоценокструктурныхпараметровуравненийсистемы),поэтомуиполучилназваниедвухшагового.

35.Оптимизационнаямодельформированияинвестиционногопортфеля.

3.3Нахождениеоптимальногопортфеля

ВтеорииМарковицаинвесторыстремятсясформироватьпортфельценныхбумаг,чтобымаксимизироватьполучаемуюполезность.Инымисловами,каждыйинвесторжелаеттакимобразомсформироватьпортфель,чтобысочетаниеожидаемойдоходностиE(r)иуровнярискаσпортфеляприносилобыемумаксимальноеудовлетворениепотребностейиминимизировалорискприжелаемойдоходности.РазныеинвесторыимеютотличныедруготдругамненияобоптимальностисочетанияE(r)иσ,посколькуотношениеодногоинвесторакрискунепохоженажеланиерисковатьдругогоинвестора.Поэтому,говоряобоптимальномпортфеле,надоиметьввиду,чтоэтакатегориясугубоиндивидуальна,иоптимальныепортфелиразныхинвесторовтеоретическиотличаютсядруготдруга.Темнеменеекаждыйоптимальныйпортфельнепременноявляетсяэффективным,тоестьинвесторывыбираютудовлетворяющийих(оптимальный)портфельизэффективныхпортфелей.

апрактикеконкретныйинвестор,построивграницуэффективныхпортфелей,должензадатьсебевопрос–какуюдоходностьоножидаетотпортфеля?Послеэтогопокривойграницыэффективныхонопределяетуровеньσтакогопортфеля.Затеминвестордолженоценить,удовлетворяетлиеготакойуровеньриска.Еслиинвесторготовкболеевысокомууровнюриска,тоемуцелесообразновыбратьпортфельсболеевысокойE(r).Тотпортфель,которыйприустановленнойинвесторомдоходностиE(r)дастнаилучшеесочетаниеE(r)иσ,будетоптимальным,дляданногоинвестора.

4.ОптимизацияинвестиционногопортфеляпометодуШарпа

В1963г.американскийэкономистУ.Шарп(WilliamSharpe)предложилновыйметодпостроенияграницыэффективныхпортфелей,позволяющийсущественносократитьобъемынеобходимыхвычислений.ВдальнейшемэтотметодмодифицировалсяивнастоящеевремяизвестенкакодноиндекснаямодельШарпа(Sharpesingle-indexmodel).

ВосновемоделиШарпалежитметодлинейногорегрессионногоанализа,позволяющийсвязатьдвепеременныевеличины-независимуюХизависимуюYлинейнымвыражениемтипаY=а+рХ.ВмоделиШарпанезависимойсчитаетсявеличинакакого-торыночногоиндекса.Таковымимогутбыть,например,темпыроставаловоговнутреннегопродукта,уровеньинфляции,индексценпотребительскихтоваровит.п.СамШарпвкачественезависимойпеременнойрассматривалнормуотдачиr_m,вычисленнуюнаосновеиндексаStandartandPoors(S&P500).Вкачествезависимойпеременнойберетсяотдачаr_iкакой-тоi-ойценнойбумаги.ПосколькузачастуюиндексS&P500рассматриваетсякакиндекс,характеризующийрынокценныхбумагвцелом,тообычномодельШарпаназываютрыночноймоделью(MarketModel),анормуотдачиr_m-рыночнойнормойотдачи.

Пустьнормаотдачиr_mпринимаетслучайныезначенияивтечениеNшаговрасчетанаблюдалисьвеличиныr_m1,r_m2,...,r_mN.Приэтомдоходностьr_iкакой-тоi-ойценнойбумагиимелазначенияr_i1,r_i2,...,r_iN.Втакомслучаелинейнаярегрессионнаямодельпозволяетпредставитьвзаимосвязьмеждувеличинамиr_mиr_iвлюбойнаблюдаемыймоментвремениввиде:

r_i,t=а_i+р_ir_m,t+8_i,t(12)

где:r_it-доходностьi-ойценнойбумагивмоментвремениt;

а_i-параметр,постояннаясоставляющаялинейнойрегрессии,показывающая,какаячастьдоходностиi-ойценнойбумагинесвязанасизменениямидоходностирынкаценныхбумагr_m;

Pi-параметрлинейнойрегрессии,называемыйбета,показывающийчувствительностьдоходностиi-ойценнойбумагикизменениямрыночнойдоходности;

r_mt-доходностьрыночногопортфелявмоментt;

е_i,t-случайнаяошибка,свидетельствующаяотом,чтореальные,действующиезначенияr_itиr_mtпороюотклоняютсяотлинейнойзависимости.

Особоезначениенеобходимоуделитьпараметрур_i,посколькуонопределяетчувствительностьдоходностиi-ойценнойбумагикизменениямрыночнойдоходности.

Вобщемслучае,если$>1,тодоходностьданнойценнойбумагиболеечувствительная,подверженабольшимколебаниям,чемрыночнаядоходностьr_m.Соответственно,приfr<1ценнаябумагаимеетменьшийразмахотклоненийдоходности_hотсреднейарифметической(ожидаемой)величиныE(r)_j,чемрыночнаянормаотдачи.Вэтойсвязиценныебумагискоэффициентомр>1классифицируютсякакболеерискованные,чемрыноквцелом,аср<1-менеерискованными.

Какпоказываютисследования,длябольшинстваценныхбумагр>0,хотямогутвстретитьсяценныебумагиисотрицательнойвеличиной

Р.

4.1Определениеожидаемойдоходностиидисперсиипортфеля

Ожидаемаядоходностьпортфеля,состоящегоизnценныхбумаг,вычисляетсяпоформуле

E(r_n)=УW_iE(r_i)(13)

i=1

гдеWi-вескаждойценнойбумагивпортфеле.Подставимвэту

формулувыражениедляr_iизформулы(12):

E(r_n)=n;W_iE(а_i+р_ir_m+б_i)=n;W_i(а_i+б_i)+n;W_i-р_гE(r_m)(14)

i=1i=1i=1

Дляприданияэтойформулекомпактности,Шарппредложилсчитатьрыночныйиндекскакхарактеристикуусловной(n+1)-ойценнойбумагивпортфеле.Втакомслучае,второеслагаемоеуравнения(14)можнопредставитьввиде:

nW_iP_iE(r_m)=W_n+1E(a_n+1+s_n+1)(15)i=1

где:W_n+1=nW_iД_i;(15a)

i=1

an+1+sn+1=rm.

приэтомсчитается,чтодисперсия(n+1)-ойошибкиравнадисперсиирыночнойдоходности:^_n+1=с£.Выражение(15a)

представляетсобойсуммувзвешенныхвеличин“беты”ф_i)каждойценнойбумаги(гдевесомслужатW_i)иназываетсяпортфельнойбетой(Р_n).Сучетомвыражений(14)и(15)формулу(13)можнозаписатьтак:

E(r_n)=хW_iE(а_i+_еi)(16)

i=1

апосколькуE(_Si)=0,тоокончательноимеем:

E(r_n)=yW_ia_i(17)

i=1Итак,ожидаемуюдоходностьпортфеляE(r_n)можнопредставитьсостоящейиздвухчастей:

а)суммывзвешенныхпараметрова_iкаждойценнойбумаги- W_1tt1+W₂a₂+....+W_na_n,чтоотражаетвкладвE(r_n)самихценных бумаг,и

б)компонентыW_n+1a_n+1=nW_iAE(r_m),тоестьпроизведения

i=1портфельнойбетыиожидаемойрыночнойдоходности,чтоотражаетвзаимосвязьрынкасценнымибумагамипортфеля.

36. Модель Марковица

Основные концепции современной теории портфеля изложены в монографии, написанной доктором Гарри Марковицем. Первоначально Марковиц предположил, что управление портфелем является проблемой структурного, а не индивидуального выбора акций, что обычно практикуется. Марковиц доказывал, что диверсификация эффективна только тогда, когда корреляция между включенными в портфель рынками имеет отрицательное значение. Если у нас есть портфель, составленный из одного вида акций, то наилучшая диверсификация достигается в том случае, если мы выберем другой вид акций, которые имеют минимально возможную корреляцию с ценой первой акции. В результате этого, портфель в целом (если он состоит из этих двух видов акций с отрицательной корреляцией) будет иметь меньшую дисперсию, чем любой вид акций, взятый отдельно. Марковиц предположил, что инвесторы действуют рациональным способои и при наличии выбора предпочитают портфель с меньшим риском при равном уровне прибыльности или выбирают портфель с большей прибылью, при одинаковом риске. Далее Марковиц утверждает, что для данного уровня риска есть оптимальный портфель с наивысшей доходностью, и таким же образом для данного уровня доходности есть оптимальный портфель с наименьшим риском. Портфель, доходность которого может быть увеличена без сопутствующего увеличения риска или портфель, риск которого можно уменьшить без сопутствующего уменьшения доходности, согласно Марковицу, неэффективны. Рисунок 1-7 показывает все имеющиеся портфели, рассматриваемые в данном примере. Если у вас портфель С, то лучше заменить его на портфель А, где прибыль такая же, но с меньшим риском, или на портфель В, где вы получите большую прибыль при том же риске. Описывая эту ситуацию, Марковиц ввел понятие «эффективная граница» (efficient frontier). Это набор портфелей, которые находятся в верхней левой части графика, то есть портфели, прибыль которых больше не может быть увеличена без увеличения риска, и риск которых не может быть уменьшен без уменьшения прибыли. Портфели, находящиеся на эффективной границе, называются эффективными портфелями (см. Рисунок 1-8).

Портфели, которые находятся вверху справа и внизу слева, в целом недостаточно диверсифицированы по сравнению с другими портфелями. Те же портфели, которые находятся в середине эффективной границы, обычно очень хорошо диверсифицированы. Выбор портфеля инвестором зависит от степени неприятия риска инвестором — иначе говоря, от желания взять на себя риск. В модели Марковица любой портфель, который находится на эффективной границе, является хорошим выбором, но какой именно портфель выберет инвестор — это вопрос личного предпочтения (позднее мы увидим, что есть точное оптимальное расположение портфеля на эффективной границе для всех инвесторов).

Модель Марковица первоначально была представлена для портфеля акций, который инвестор будет держать достаточно долго. Поэтому основными входными данными были ожидаемые доходы по акциям (определяется как ожидаемый прирост цены акции плюс дивиденды), ожидаемые дисперсии этих доходов и корреляции доходов между различными акциями. Если бы мы перенесли эту концепцию на фьючерсы, то было бы разумным (так как по фьючерсам не выплачивают дивидендов) измерять ожидаемое повышение цены, дисперсию и корреляции различных фьючерсов. Возникает вопрос: «Если мы измеряем корреляцию цен, то что произойдет при включении в портфель двух систем с отрицательной корреляцией, работающих на одном и том же рынке?»