
- •Содержание
- •1. Функция. Основные определения. Последовательность. Предел последовательности
- •2. Предел функции непрерывного аргумента
- •3. Вычисление пределов функций. Основные приёмы
- •4. Замечательные пределы
- •5. Применение эквивалентных бесконечно малых к нахождению пределов функции. Сравнение бесконечно малых
- •6. Непрерывность функций. Точки разрывa.
- •Список литературы
- •Введение в математический анализ. Пределы
- •443086 Самара, Московское шоссе,34.
- •443086 Самара, Московское шоссе,34.
Государственное образовательное учреждение
Высшего профессионального образования
«Самарский Государственный аэрокосмический
университет имени академика С.П. Королева»
(национальный исследовательский университет)
Введение в математический анализ. Пределы
Утверждено Редакционно-издательским советом в качестве методических указаний
Самара
Издательство СГАУ
2010
УДК СГАУ:519.24(075)
ББК22.1
Составитель: Кузнецова С.И.
Рецензент: к.т.н., доцент Шопин Г.П.
Введение в математический анализ. Пределы: метод. указания/сост. Кузнецова С.И. – Самара: изд-во Самар. гос. аэрокосм. ун-та, 2010.-36с.
Методические указания составлены в соответствии с действующей программой по курсу высшей математики для инженерно-технических специальностей Самарского государственного аэрокосмического университета. Указания обеспечивают полную теоретическую и методическую поддержку практических занятий по темe « Введение в математический анализ. Пределы».
Методические указания могут быть рекомендованы студентам для самостоятельной работы и подготовки к экзаменам.
УДК СГАУ:519.24(075)
ББК22.1
©Самарский государственный
аэрокосмический университет, 2010
Содержание
1. Функция. Основные определения. Последовательность. Предел последовательности 4
2. Предел функции непрерывного аргумента 17
3. Вычисление пределов функций. Основные приёмы 27
4. Замечательные пределы 34
5. Применение эквивалентных бесконечно малых к нахождению пределов функции. 39
Сравнение бесконечно малых 39
6. Непрерывность функций. Точки разрывa. 49
Список литературы 56
1. Функция. Основные определения. Последовательность. Предел последовательности
Если
каждому значению переменной х,
принадлежащему некоторой области,
соответствует одно определенное значение
другой переменной у,
то у
есть функция от х,
 .
.
Переменная
х
называется независимой переменной или
аргументом. Зависимость переменных х
и у
-функциональная зависимость. Совокупность
значений х,
для которых определяются значения у
в силу
 называется областью определения функции
(или областью существования). Совокупность
всех значений, принимаемых переменнойу,
называется областью значений функции.
называется областью определения функции
(или областью существования). Совокупность
всех значений, принимаемых переменнойу,
называется областью значений функции.
Основные свойства функций:
1.
Четность и нечетность. Функция
 называется четной, если для любого
значенияx
из области определения
называется четной, если для любого
значенияx
из области определения и нечетной, еcли
для любого значения x
из области определения
и нечетной, еcли
для любого значения x
из области определения
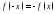 .
.
Например,
 - четная функция, потому что
- четная функция, потому что ,
график ее в декартовой системе координат
симметричен относительно оси ФОУ;
,
график ее в декартовой системе координат
симметричен относительно оси ФОУ;
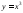 - нечетная функция,
потому что
- нечетная функция,
потому что ,
график ее в декартовой системе координат
симметричен относительно точки О(0;0);
,
график ее в декартовой системе координат
симметричен относительно точки О(0;0);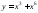 - не является четной или нечетной,
- не является четной или нечетной,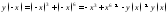 .
.
2.
Монотонность функции. Функция
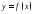 называется возрастающей, если большему
значению аргумента соответствует
большее значение функции. Функция
называется возрастающей, если большему
значению аргумента соответствует
большее значение функции. Функция называется убывающей, если большему
значению аргумента соответствует
меньшее значение функции. Возрастающие
или убывающие функции называются
монотонными.
называется убывающей, если большему
значению аргумента соответствует
меньшее значение функции. Возрастающие
или убывающие функции называются
монотонными.
Для
любой монотонной функции
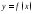 существует обратная функция
существует обратная функция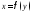 .
Значения функции
.
Значения функции для обратной к ней становятся значениями
аргумента, а значения аргумента функции
для обратной к ней становятся значениями
аргумента, а значения аргумента функции для обратной к ней становятся значениями
функции. График обратной функции в
декартовой системе координат симметричен
графику данной функции относительно
биссектрисы первого координатного
угла. Например,
для обратной к ней становятся значениями
функции. График обратной функции в
декартовой системе координат симметричен
графику данной функции относительно
биссектрисы первого координатного
угла. Например,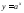 и
и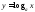 .
.
3.
Ограниченность. Функция
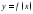 называется ограниченной сверху на
отрезке
называется ограниченной сверху на
отрезке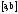 ,
если существует такое числоA,
что для всех
,
если существует такое числоA,
что для всех


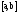 будет выполняться неравенство
будет выполняться неравенство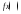 <A.
Функция
<A.
Функция
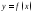 называется ограниченной снизу на отрезке
называется ограниченной снизу на отрезке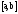 ,
если существует такое числоA,
что для всех
,
если существует такое числоA,
что для всех


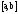 будет выполняться неравенство
будет выполняться неравенство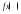 >A.
Функция
>A.
Функция
 называется ограниченной на отрезке
называется ограниченной на отрезке ,
если существует такое положительное
числоA>0,
что для всех
,
если существует такое положительное
числоA>0,
что для всех


 будет выполняться неравенство |
будет выполняться неравенство |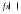 |<A.
|<A.
4.
Периодичность. Функция
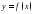 называется периодической, если существует
такое число
называется периодической, если существует
такое число
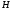 ,
что для любого значения
,
что для любого значения из области определения выполняется
равенство
из области определения выполняется
равенство .
Период
.
Период -
наименьшее положительное число
-
наименьшее положительное число
 .
.
5. Сложная функция. Пусть у является функцией от u, а u в свою очередь зависит от х, тогда у является функцией от функции или сложной функцией.
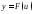 ,
,
 .
.

Например,
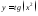 .
.
Элементарной
функцией называется функция, которая
может быть задана одной формулой вида
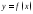 ,
где справа стоящее выражение составлено
из основных элементарных функций и
постоянных при помощи конечного числа
операций сложения, вычитания, умножения,
деления и взятия функции от функции.
Основными элементарными функциями
являются следующие: степенная,
показательная, логарифмическая,
тригонометрическая, обратная
тригонометрическая.
,
где справа стоящее выражение составлено
из основных элементарных функций и
постоянных при помощи конечного числа
операций сложения, вычитания, умножения,
деления и взятия функции от функции.
Основными элементарными функциями
являются следующие: степенная,
показательная, логарифмическая,
тригонометрическая, обратная
тригонометрическая.
Пример
1.
Дана
функция
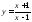 ,
найти
,
найти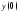 ,
,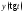 :
:
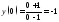 ;
;
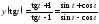
Пример
2.
Дана
функция:
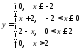
Найти y(-1); y(3).
На рис.1 изображен график заданной функции:

Рис 1.
y(-1)=1; y(3)=0
Пример
3.
Записать
в виде цепочки основных элементарных
функций
 :
:
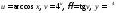 .
.
Пример
4.
Найти
область определения функции
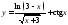 :
:
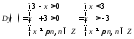
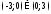 .
.
Пример
5.
Перечислить
свойства функции
 :
:
четная,
 ;
;
ограниченная,
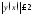 ;
;
периодическая,
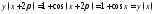 ,
,
 ,
,
 -наименьший
период.
-наименьший
период.
Последовательность. Предел последовательности
Последовательностью
действительных чисел называется функция,
определенная на множестве всех натуральных
чисел. Число
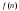 называетсяn-м
членом последовательности и обозначается
символом
называетсяn-м
членом последовательности и обозначается
символом
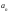 ,
а формула
,
а формула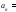
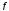 (n)
называется формулой общего члена
последовательности
(n)
называется формулой общего члена
последовательности
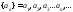
Если
для любого n
будет выполняться условие
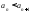 ,
то последовательность возрастающая;
если
,
то последовательность возрастающая;
если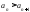 ,
то убывающая.
,
то убывающая.
Рассмотрим
последовательность, заданную
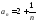

Каждый последующий член этой последовательности меньше предыдущего, это убывающая последовательность.
Число
А называется пределом числовой
последовательности
 ,
если для любого сколь угодно малого
числа
,
если для любого сколь угодно малого
числа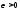 найдется такой номерN,
что для всех членов последовательности
с номерами n>N
справедливо неравенство
найдется такой номерN,
что для всех членов последовательности
с номерами n>N
справедливо неравенство
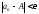 ,
,

Если последовательность имеет предел, она называется сходящейся, если не имеет – расходящейся.
Пример
6.
Написать
первые шесть членов последовательности
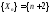
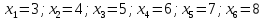
это возрастающая неограниченная последовательность (рис.2).

Рис.2
Пример 7. Написать формулу общего члена последовательности:
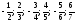 .
.
Ответ:
 .
.
Пример
8.
Используя
определение, доказать, что последовательность,
заданная формулой
 имеет предел, равный
имеет предел, равный .
.
Чтобы
показать, что
 ,
надо в соответствии с определением по
произвольному
,
надо в соответствии с определением по
произвольному >0
суметь найти такой номерN=N(
>0
суметь найти такой номерN=N( ),
чтобы для всехn>N
выполнялось неравенство
),
чтобы для всехn>N
выполнялось неравенство
| |<
|< (1)
,
(1)
,
преобразуем
| |
<
|
< .
.
Так
как n-натуральное
число, то
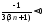 ,
следовательно
,
следовательно
|
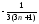 |=
|=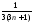 .
.
Таким образом, получаем
 <
< ,
,
3n+1>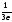 ,
,
3n>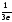 -1,
-1,
n>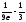 .
.
Следовательно,
если положить N( )=[
)=[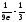 ]
([ ]-целая часть), то при всехn>N
неравенство (1) будет выполняться. Таким
образом, по произвольно заданному числу
]
([ ]-целая часть), то при всехn>N
неравенство (1) будет выполняться. Таким
образом, по произвольно заданному числу
 >0
мы можем найти такой номерN=N(
>0
мы можем найти такой номерN=N( )
(а именно,N=
)
(а именно,N=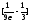 ),
что при всехn>N
будет выполняться неравенство |
),
что при всехn>N
будет выполняться неравенство | |<
|< ,
следовательно, по определению предела
,
следовательно, по определению предела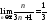 ,
что и требовалось доказать.
,
что и требовалось доказать.
Пример
9.
Показать,
что при
 последовательность с общим членом
последовательность с общим членом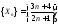 имеет пределом число 3/2.
имеет пределом число 3/2.
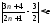 ;
;
 ;
;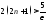 ;
; .
.
Итак,
если
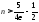 ,
то
,
то ,
т.е.
,
т.е.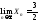
Полагая
 ,
заключаем, что неравенство
,
заключаем, что неравенство выполняется при
выполняется при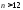 (например, при
(например, при ).
Аналогично, неравенство
).
Аналогично, неравенство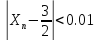 выполняется при
выполняется при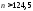 (п=125), а неравенство
(п=125), а неравенство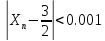 - при
- при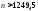 (п=1250).
(п=1250).
Задания для самостоятельной работы.
№1.
Дана функция
 .
Найти а)
.
Найти а)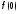 ;
б)
;
б)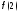 ;
в)
;
в)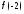 ;
г)
;
г)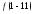 .
.
№2.
Дана функция
 .
Найти а)
.
Найти а)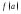 ;
б)
;
б) ;
в)
;
в) ;
г)
;
г) .
.
№3.
Дана функция
 .
.
Найти: а)y(4); б)y(0); в)y(-4).
№4.
Записать в виде цепочки основных
элементарных функций
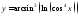 .
.
№5.
Записать в виде одной функции цепочку
функций
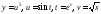 .
.
№6. Найти область определения функций:
а)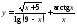 ; б)
; б)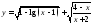 ;
;
в) ; г)
; г) .
.
№7. Перечислить свойства функций:
а)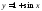 ; б)
; б)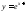 ;
;
в) ; г)
; г) .
.
№8. Написать первые шесть членов последовательностей, изобразить их на чертеже:
а)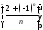 ;
б)
;
б) ;
в)
;
в) ;
г)
;
г)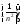 .
.
№9. Написать формулу общего члена последовательности:
а)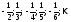 ;
б)
;
б) ;
в)
;
в)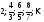
№10.
С помощью определения предела
последовательности доказать, что
последовательность с общим членом
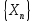 имеет предел а. Найти
имеет предел а. Найти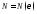 ,
взяв
,
взяв 0,1;
0,01; 0,001; 0,0001, результаты записать в
таблицу:
0,1;
0,01; 0,001; 0,0001, результаты записать в
таблицу:
|
|
0,1 |
0,01 |
0,001 |
0,0001 |
|
|
|
|
|
|
а)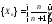 ,
а=1.
,
а=1.
б) ,
а=2;
,
а=2;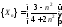 ,
а
,
а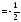 .
.


