5. Применение эквивалентных бесконечно малых к нахождению пределов функции. Сравнение бесконечно малых

Определение. Функция называется бесконечно малой приили, еслиили.

Например, бесконечно малая при;- бесконечно малая при.

Функция 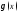называется бесконечно большой величиной приили, если для нее выполняются условияили.

Например, при;при.

Пусть и- бесконечно малые при.

1. Если , тоявляется бесконечно малой высшего порядка по сравнению с,.

2. Если , гдеm – число, отличное от нуля, то и- бесконечно малые одного порядка. В частности, если, тои- эквивалентные бесконечно малые,~.

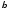3. Бесконечно малая называется бесконечно малойk- го порядка относительно бесконечно малой ,еслии- бесконечно малые одного порядка, т. е. если=А0.

Таблица эквивалентных бесконечно малых:

1)~,→0;

2) ~,→0;

3)~,→0;

4) ~,→0;

5) ~,→ 0;

6)~,→0;

7) ~α, →0;

8) ~,→0;

9)~,→0.

Пример 1. Найти

= =

Пример 2. Найти

Так как х → 0, то 3→ 0, (- 2) → 0, поэтому

Пример 3. Найти

Воспользуемся теоремами:

1) Алгебраическая сумма конечного числа бесконечно малых величин эквивалентна сумме части слагаемых, имеющих низший порядок малости.

2) Предел частного двух бесконечно малых величин равен пределу частного двух соответственно эквивалентных бесконечно малых величин.

1 - cos ~ ;ln(l + З) ~З;sin² ~ ²; -1 ~ tg² ~ ²

.

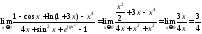Пример 4. Сравнить бесконечно малые величины =sin² и = 2sin при→0,

Таким образом, α=0(β), α является бесконечно малой высшего порядка по сравнению с β.

Пример 5. Сравнить ипри

.

Существует конкретное число k, когда

при k=2, ,, следовательно,- бесконечно малая величина второго порядка по сравнению с.

Пример 6. Доказать, что при →1 бесконечно малые величины α() = (1-) и β()=1-будут одного порядка малости.

α() и β() будут одного порядка малости, если тогдатогда

Следовательно, α() и β() одного порядка малости.

Пример 7. Сравнить бесконечно малые величины ипри→0.

, т. к. при→0;

;

.

Таким образом, , следовательно, α() и β() – эквивалентны.

Пример 8. Сравнить бесконечно малую величину с бесконечно малой()=при→0.

Тогда,

Таким образом, α=0(β), α является бесконечно малой высшего порядка по сравнению с β.

Задания для самостоятельной работы.

Вычислить пределы, пользуясь эквивалентными бесконечно малыми величинами:

1) 2)

3)

4)

5)

Сравнить бесконечно малые величины при →0:

6) sin+tg2и 3;7) tg2+3² и +²;

8) ln(l + ²) и arcsin () ; 9)-1 и хlna;

10) Сравнить ипри;

11) При каких х функции будут бесконечно малыми?

a) ; б); в); г);

12) При каких х функции будут бесконечно большими?

a) 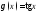; б);

в) ; г).

6. Непрерывность функций. Точки разрывa.

Функция называется непрерывной в точкеа, если

1) эта функция определена в некоторой окрестности точки а;

2) существует предел ;

3) этот предел равен значению функции в точке а, т.е. .

Обозначая -а =Δx и f(x)- f(a) =Δy, условие непрерывности можно записать так: Δy = 0.

Если функция непрерывна в каждой точке некоторой области, то она непрерывна в этой области.

Точка а, принадлежащая области определения функции или являющаяся граничной для этой области, называется точкой разрыва, если в этой точке нарушается условие непрерывности функции.

Если существуют конечные пределы и, причем не все три числаf(a), f(a - 0), f(a + 0), равны между собой, то а называется точкой разрыва I рода.

Точки разрыва I рода подразделяются на точки устранимого разрыва (когда f(a-0) = f(a + 0)≠ f (a )) и точки скачка (когда f(a - 0) ≠ f(a + 0)), f(a + 0)-f(a-0)) - скачок функции в точке а. Точки разрыва, не являющиеся точками разрыва I рода, называются точками разрыва II рода. В точках разрыва II рода не существует хотя бы один из односторонних пределов.

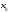Пример 1. Доказать, что функция = З-4 непрерывна в точке=2.

Область определения нашей функции D(f) = (-;+) , следовательно функция определена в точке x₀ и в окрестности точки .

f(2) = 2,

Условие выполнено, следовательно, данная функция непрерывна в точке =2.

Пример 2. Доказать, что функция = 7² -3 непрерывна на интервале (-;+).

Для доказательства непрерывности функции на (-;+) надо доказать непрерывность ее в произвольной точке х (-;+), надо доказать Δy = 0.

Область определения нашей функции - вся числовая ось.

Δf= f(x + Δх)- f(x) = (7(+ Δ)² -3)-(7² - 3) = 7х² + 14хΔх +

+ 7 Δ² - 3 - 7х² + 3 = 14Δ+ 7Δ² = 7Δ(2+ Δх)

Δy =7Δ(2+ Δх) = 0

Следовательно, f(x)=7x²-3 непрерывна в любой точке интервала и тогда непрерывна на всем интервале.

Пример 3. Исследовать на непрерывность функцию

Рис. 7

Всякая элементарная функция непрерывна в своей области определения. Данная функция задается различными формулами на разных участках, следовательно, не является элементарной.

Однако, если разбить область определения D(f)= на отдельные интервалыD₁(f) =; .D₂(f) =;D ₃(f)= ,то на каждом из этих интервалов функцияf(x) окажется элементарной и, следовательно, непрерывной.

Таким образом, осталось исследовать граничные точки.

1. x₁ =0, f(x₁)= f(x₂)=0

Таким образом, в точке х₁, функция непрерывна.

2)_{= 1}

Пределы слева и справа в точке ₂ не равны между собой, таким образом, точка ₂ - точка разрыва 1 рода.

=5-2=3- скачок функции в точке ₂ .

Пример 4. Найти и классифицировать точки разрыва функции y=

В точках =1 и =5 функция не определена.

1) = 1

2) =5

Обе точки =1 и =5 - точки разрываII рода.

Пример 5. Показать, что при х=3 функция у = имеет устранимый разрыв.

В точке , =3 функция не определена. В других точках дробь можно сократить на-3≠0, следовательно,у = х + 3 во всех точках х≠З,

Функция в точке =3 имеет устраняемый разрыв.

Он будет устранен, если условиться, что при =3 значение функции равно 6.

Задания для самостоятельной работы.

1. Исследовать на непрерывность f(x)= точке₀=2;

2. Доказать непрерывность функции f(x) = +ln(l + х) в области (-1;+оо);

3. Исследовать на непрерывность функцию:

3. Исследовать характер точки разрыва функции

;

5)Найти точки разрыва: а)б).