13. Аналитическое выражение первого начала термодинамики

Значения удельных внутренней энергии и энтальпии простого тела однозначно определяются двумя независимыми переменными и могут быть представлены следующим образом:

;

Изменения внутренней энергии и энтальпии простого тела, как функций состояния, в элементарных процессах являются полными дифференциалами и определяются соотношениями

;

Д ля изохорного процесса ( ) частная производная внутренней энергии по температуре равна истинной изохорной теплоемкости а для изобарного процесса ( ) частная производная энтальпии по температуре равна истинной изобарной теплоемкости

В результате подстановки выражение (1) и (2) в уравнение и разделения переменных

Аналитической форме.

Выражения в квадратных скобках в литературе часто называют калорическими коэффициентами,

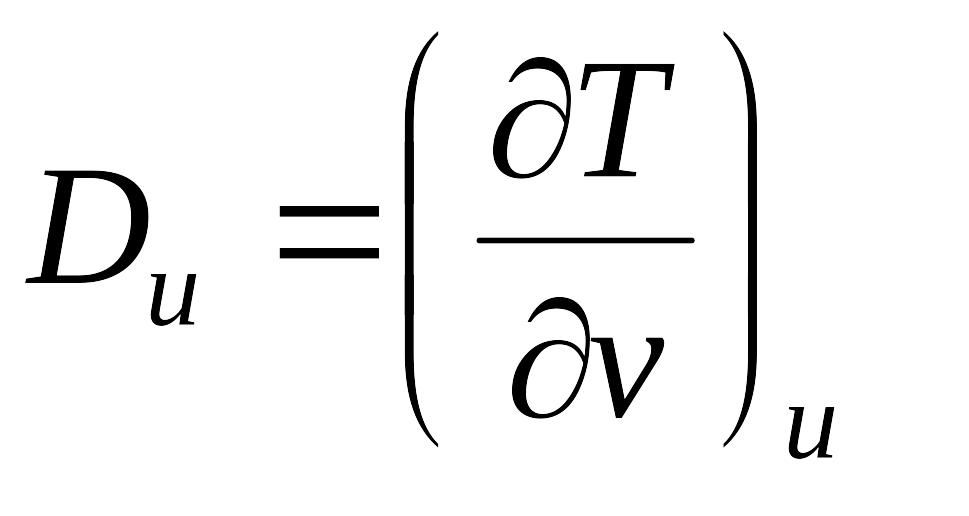
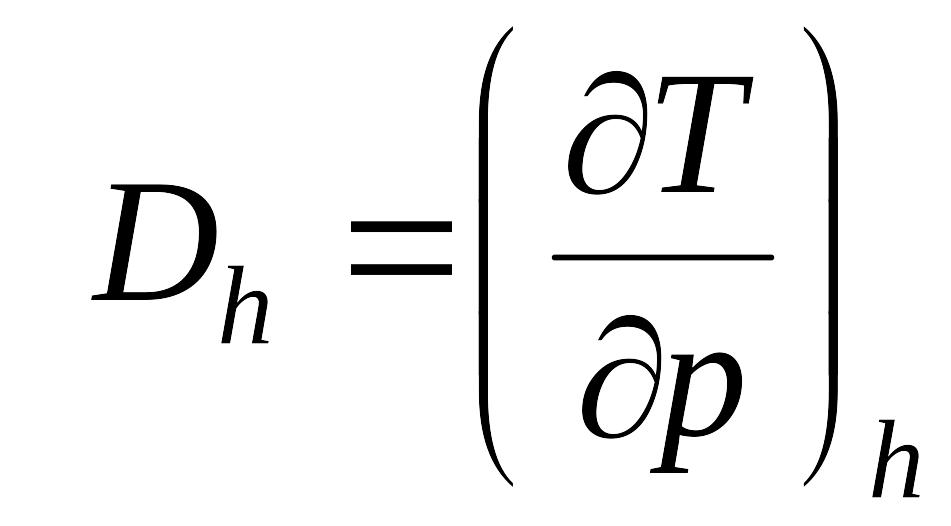
Коэффициент Джоуля - Гей Люссака коэффициент Джоуля-Томсона

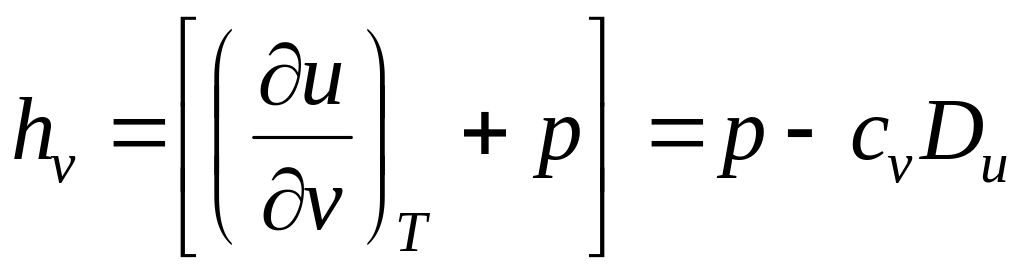
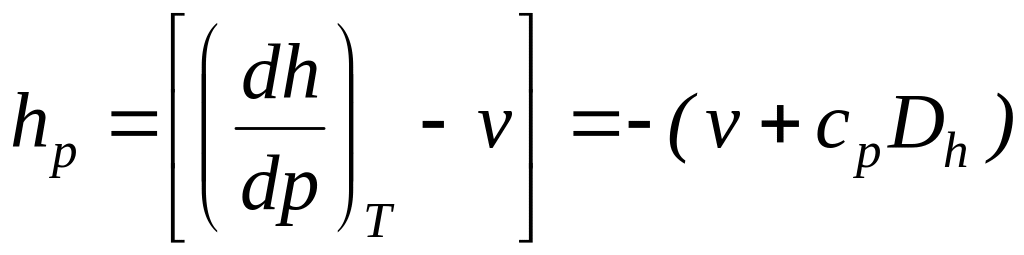
14. Первое начало термодинамики для идеального газа.

Идеальный газ – система, которая подчиняется уравнению Менделеева-Клаперона: и внутренняя энергия системы зависит только от температуры .

Первое начало термодинамики для простого тела: . Для идеального газа: , , , . Получим:

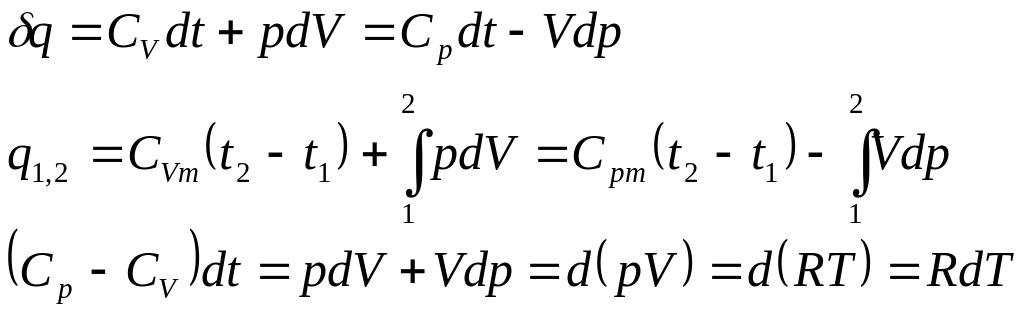Получили закон Майера: .

Универсальная газовая постоянная .

1 5. Принцип существования энтропии идеального газа.

Энтропия , . Удельная энтропия ,

Принципом существования энтропии идеального газа

Энтропия всё время возрастает. В изолированной системе энтропия может оставаться постоянной.

При и температуре удельная энтр .

, где - вторая средняя теплоёмкость или logарифмет. теплоёмкость.

Так как , то если энтропия растёт, то есть , то тепло подводится, то есть .

Уравнение, определяющее энтропию (полученное)

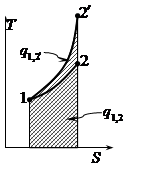
Термодинамические процессы изменения состояния простого тела

Название и уравнение процесса	Показатель Политропы	Графическое изображение	Работа	Количество теплоты	Координаты T-S
1	2	3	4	5
Политропный pvn = idem	-  n  +, n =		l1,2 = , w1,2 = n , 1,2 = = = = =	q1,2 = u1,2 + l1,2 = = h1,2 + w1,2 , q1,2 =
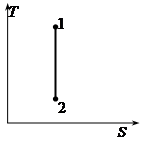
Изобарный p = idem, dp = 0	n = 0		l1,2 = p(v2 - v1), w1,2 = 0, 1,2 = =	q1,2 = u1,2 + l1,2 = = h1,2	1-2 – изобарный процесс

1	2	3	4		1-2’ – изохорный процесс
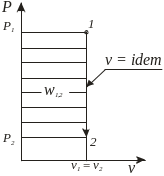
Изохорный v = idem, dv = 0	n = ± ∞		l1,2 = 0, w1,2 = v(p1 - p2), 1,2 = =	q1,2 = u1,2 = h1,2 + w1,2
Изопотенциаль-ный pv = idem	n = 1		l1,2 = w1,2 = = pvln = pvln , 1,2 = 1	q1,2 = u1,2 + l1,2 = = h1,2 + w1,2
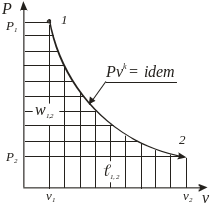
Адиабатный δq = 0, pvk = idem	n = k = ns =		l1,2 = , w1,2 = k , 1,2 = = = = =	q1,2 = 0

27-30. Политропа с постоянным показателем.

Политропным процессом с постоянным показателем называется обратимый термодинамический процесс изменения состояния простого тела.

Уравнение политропного процесса с постоянным политропным показателем:

где - политропный показатель, являющий в рассматриваемом процессе постоянной (-  n  +). Физический смысл показателя политропы п определяется после дифференцирования выражения

Тогда:

Следовательно постоянный показатель политропы определяется соотношением потенциальной и термодинамической работ в элементарном или конечном процессах.

Показателем политропного процесса является линейная зависимость от , то есть: .

1. 2. -истинный

показатель политропы. - второй средний показатель политропы. - первый средний показатель политропы.

П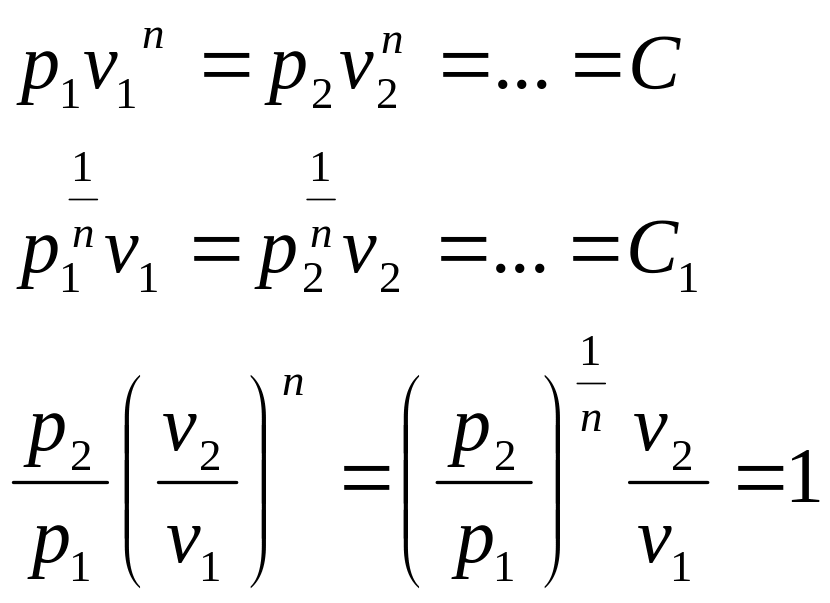 ри этом политропный показатель может принимать значения в пределах от минус бесконечности до плюс бесконечности и оставаться постоянным в течение процесса. Если , то , следовательно , то есть процесс изохорический. Если , то , следовательно , то есть процесс изобарический. Если , то , следовательно . Так как для идеального газа , то .

Если уравнением процесса является уравнение , то в этом процессе , следовательно , то есть процесс изоэнергетический.

Для идеального газа , следовательно , то есть процесс изоэнтальпийный.

, - показатель адиабаты, - политропы, изоэнергетического процесса.

Для адиабатического процесса .

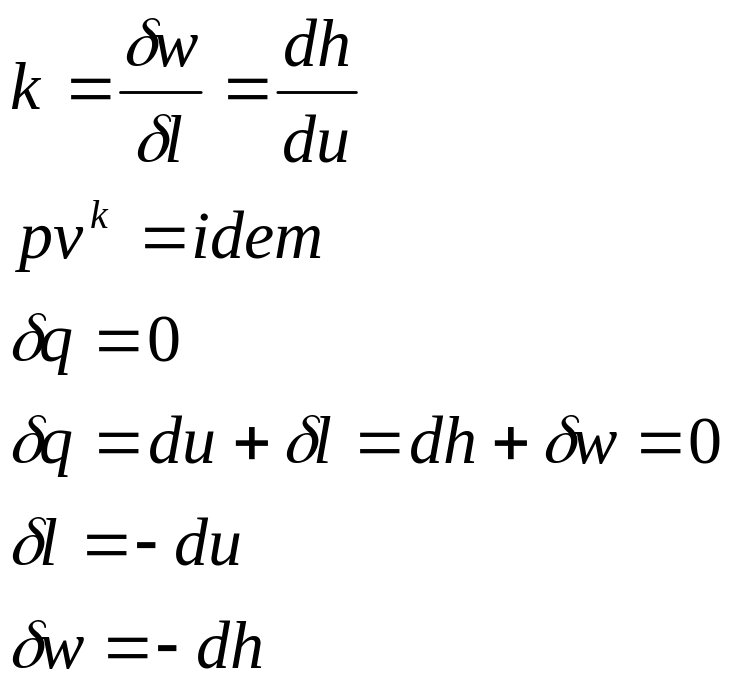
Все уравнения для политропного процесса остаются справедливы и для адиабатического процесса, только вместо политропного показателя используют адиабатический показатель.

Для идеального газа и

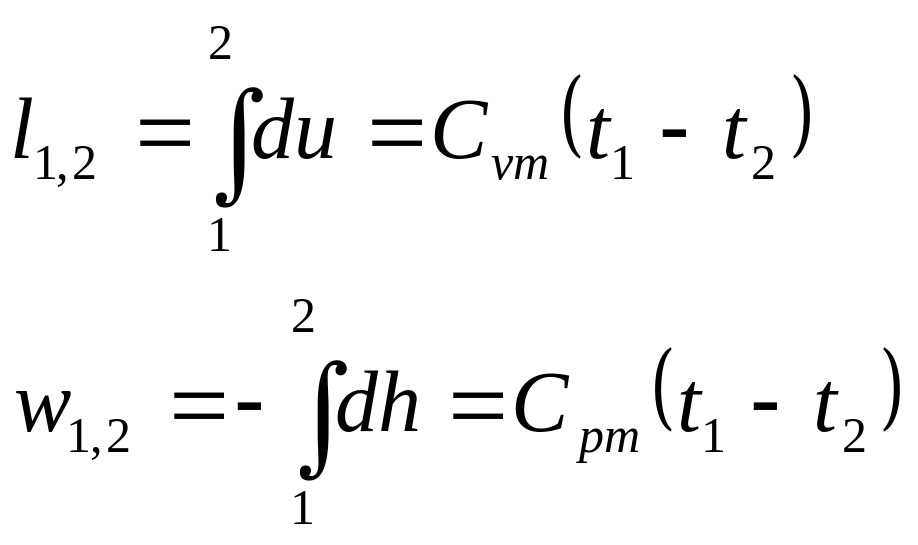
Характеристика растяжения (сжатия).

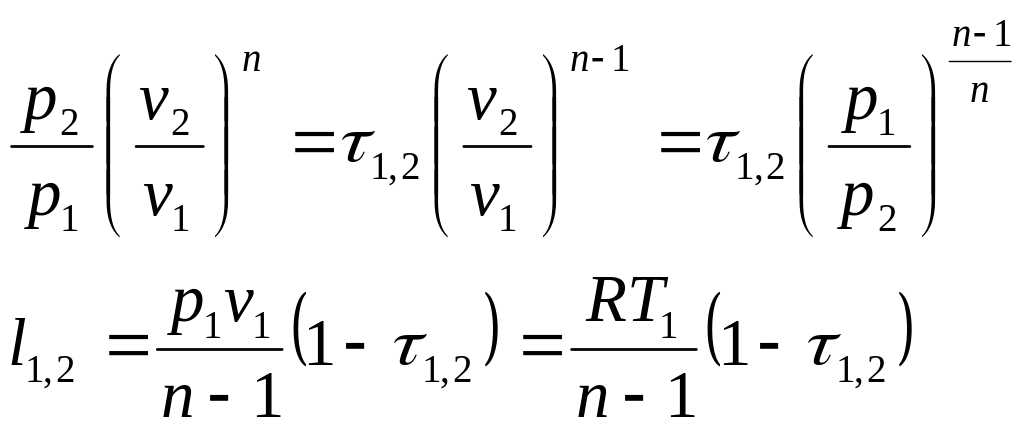
- для идеального газа.

Выражения конечных (интегральных) величин термодинамической и потенциальных работ в политропных процессах можно получить при сопоставлении их элементарных значений: ; .

После подстановки выражения для показателя политропы

, или \ .

Интегрируя последнее выражение с учетом того, что процесс подчиняется уравнению политропы с постоянным показателем (n=idem), получаем следующее соотношение для определения удельной термодинамической работы в конечном процессе (1-2)

.

Выражения конечных (интегральных) величин термодинамической и потенциальных работ в политропных процессах рассчитываются по следующим соотношениям

. (1.102)

, (1.103)

где – характеристика процесса расширения или сжатия.

Соотношение для определения характеристики расширения или сжатия в рассматриваемом процессе определяется с учетом зависимостей (1.101а) и имеет следующий вид:

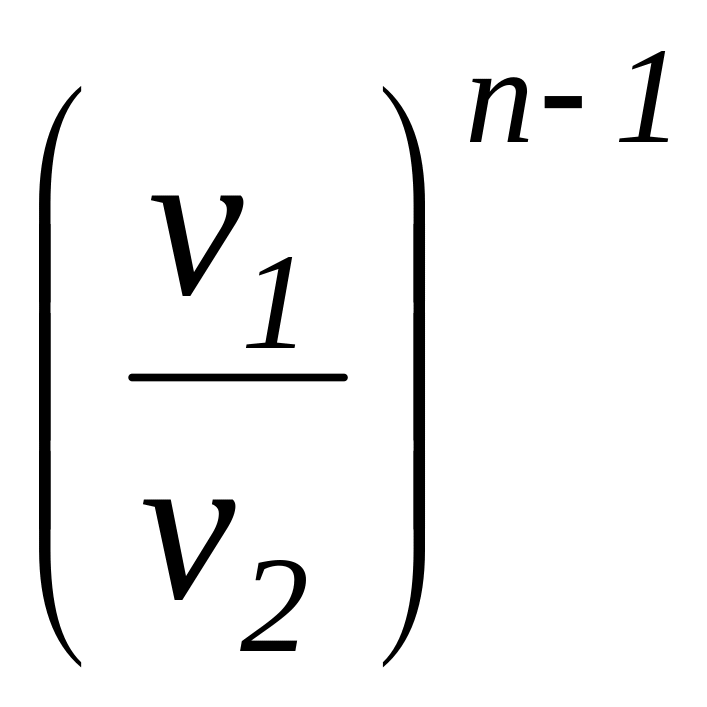= = . (1.104)

Расчетное выражения теплообмена для простых тел выводится на основе рассмотрения выражения первого начала термодинамики и имеет следующий вид

. ,

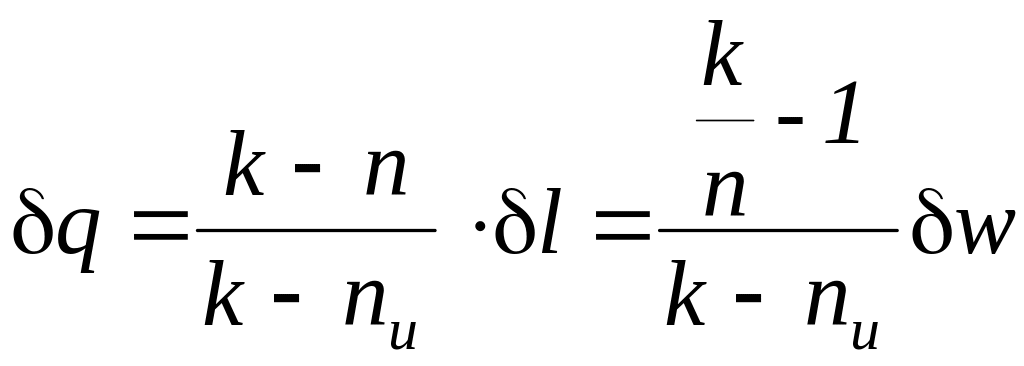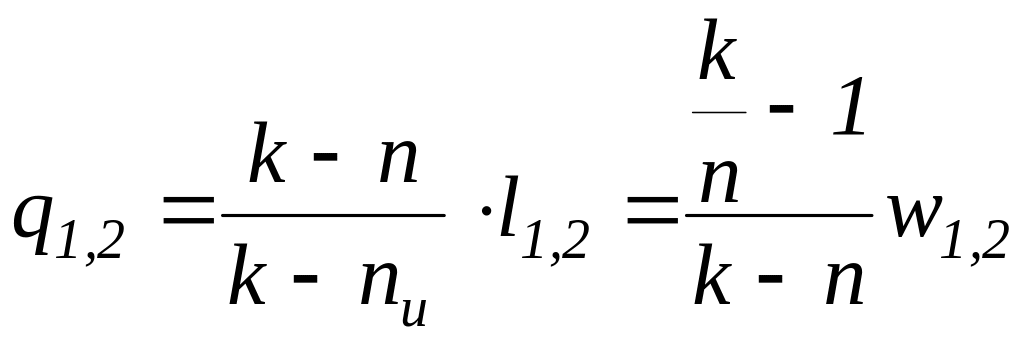где k – показатель адиабаты, n – показатель политропы, n_u – показатель изоэнергетического процесса.
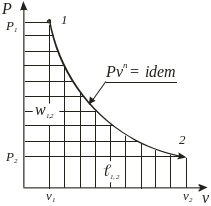
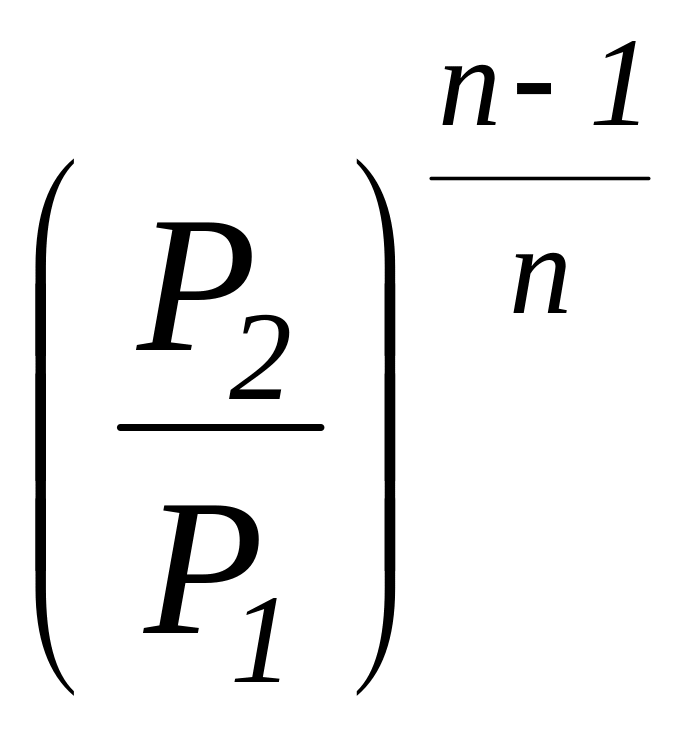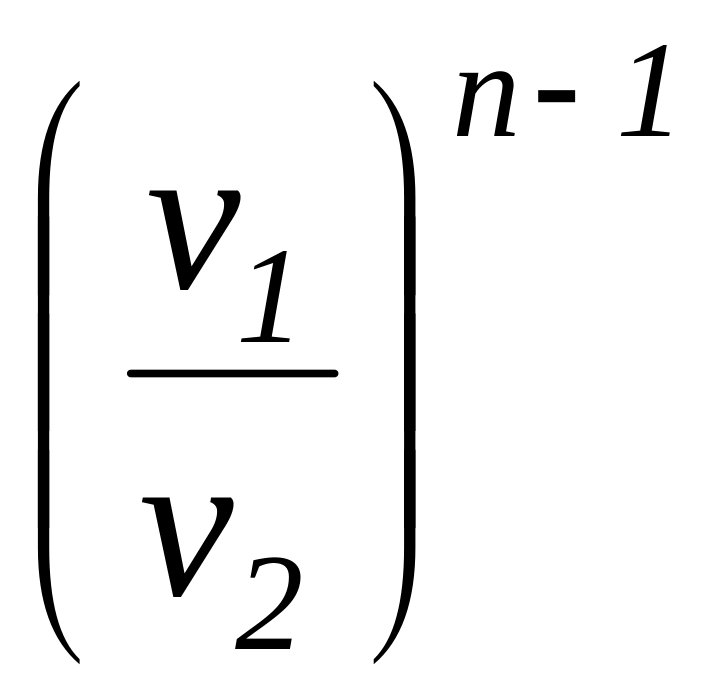
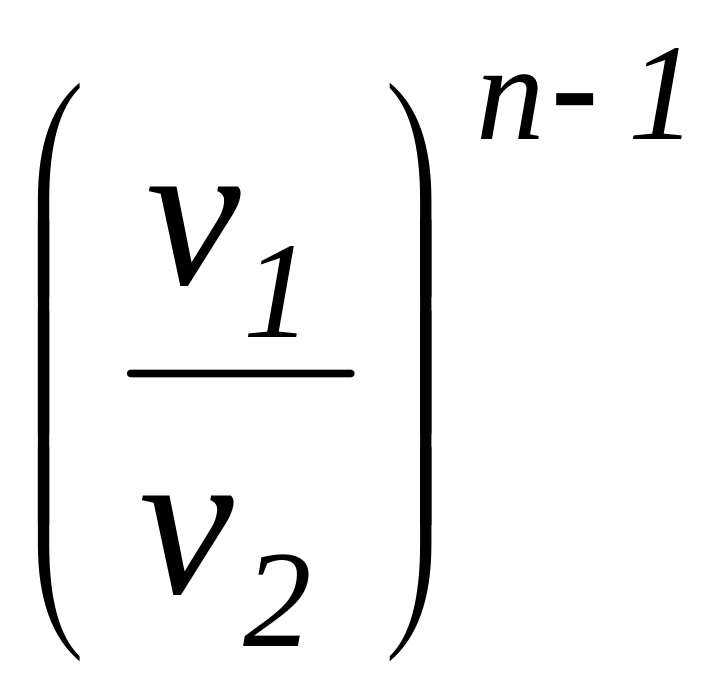
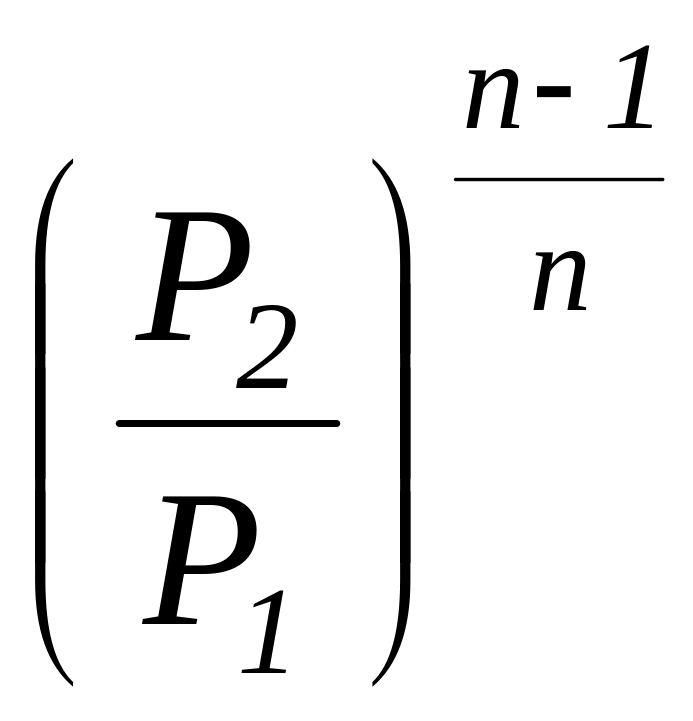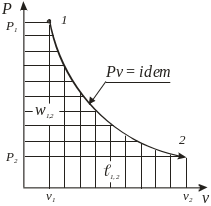
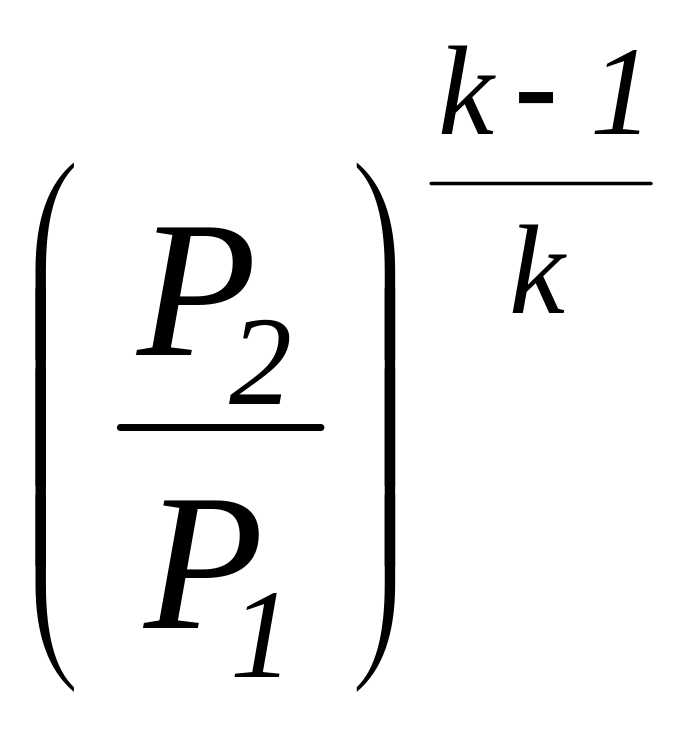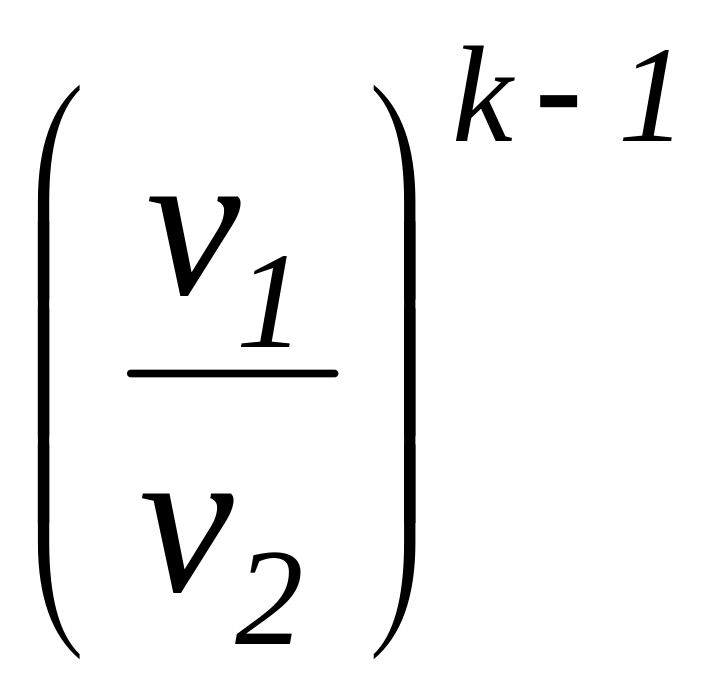