Вопрос 11. Теория соответственных состояний. Коэффициент сжимаемости.
В инженерных расчетах часто пользуются уравнением состояния идеального газа с введением в него поправочного коэффициента (z), называемого коэффициентом сжимаемости
.
Коэффициент сжимаемости (z) учитывает различие между идеальным и реальными газами (для идеального газа z = 1).
Коэффициент сжимаемости является функцией давления, температуры и зависит от природы газа.
Для обобщения данных по коэффициентам сжимаемости различных газов был использован принцип «соответственных» состояний, сформулированный Ван-дер-Ваальсом. Принцип «соответственных» состояний утверждает, что критическое состояние действительно является одинаковым для всех веществ.
В
критической точке для всех веществ r
= 0,
,
,
.
Вещества находятся в соответственных
состояниях при одинаковом удалении от
критической точки.
Степень удаления от критической точки определяется с помощью приведенных параметров:
приведенного
давления
;
приведенной температуры
;
приведенного
объема
.
Уравнение
состояния, записанное в виде F
(
)
= 0, называется приведенным
уравнением состояния.
Оно не содержит индивидуальных констант
вещества.
Состояния
вещества, в которых они имеют одинаковые
и
называются соответственными. Зная
параметры
и
по данным рис. 1.4 определяется коэффициент
сжимаемости z.
12. Математическое выражение 1го начала термодинамики (+баланс рабочего тела).
Первое начало термодинамики – это количественное выражение закона сохранения и превращения энергии.
Закон сохранения и превращения энергии является универсальным законом природы и применим ко всем явлениям. Он гласит: «запас энергии изолированной системы остается неизменным при любых происходящих в системе процессах; энергия не уничтожается и не создается, а только переходит из одного вида в другой».
Это утверждение и принимается в качестве постулата первого начала термодинамики
Первое начало термодинамики как математическое выражение закона сохранения и превращения энергии:
Внутренняя энергия
изолированной системы сохраняет своё
постоянное значение при всех изменениях,
протекающих внутри системы, то есть
.
Изменение внутренней энергии
неизолированной системы складывается
из подведённой (отведённой) теплоты и
подведённой (отведённой) работы, то есть
.
в интегральной форме:
-
эффективная работа;
-
внешний теплообмен
Полученные уравнения учитывают только внешние эффекты и справедливы только для обратимых процессов.
У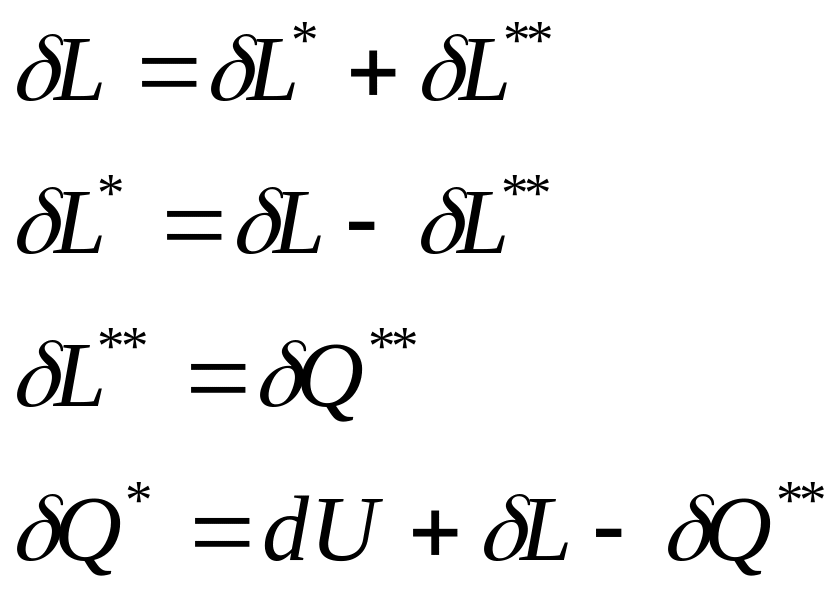
равнения
являются математическим выражением
первого начала термодинамики по внешнему
балансу теплоты и работы и гласят:
количество теплоты, подведенное извне,
идет на изменение внутренней энергии
системы и совершение работы.
В термодинамике приняты следущие знаки при определении работы и теплоты в уравнениях первого начала термодинамики: если работа выполняется телом, то она положительная; если работа подводится к телу, то она отрицательная. Если теплота сообщается телу, она имеет положительное значение; если теплота отводится от тела, она имеет отрицательное значение.
=
+
Первого начала термодинамики по
внешнему балансу.
Работа
необратимых потерь
,
связанная с затратами энергии на
преодоление сил трения, удары и завихрения,
превращается в теплоту внутреннего
теплообмена (
)
=
.
Полное
количество теплоты
,
полученное
телом, равно сумме теплоты, подведенной
извне
,
и теплоты
внутреннего теплообмена
.
;
.
Уравнения (1.55) и (1.56) называются уравнениями первого начала термодинамики по балансу рабочего тела, и справедливы для реальных процессов.
Первое начало термодинамики
по балансу рабочего тела:
,
где
- полный или приведённый теплообмен.
Полное количество теплоты , полученное телом, равно сумме теплоты, подведенной извне , и теплоты внутреннего теплообмена
Первое начало термодинамики по балансу рабочего тела справедливо для любых процессов протекающих в системе.
В условиях обратимого
процесса, то есть
,
первое начало термодинамики по балансу
рабочего тела переходит в первое начало
термодинамики по внешнему балансу. Для
использования этого уравнения нужно
уметь его интегрировать. При интегрировании
получится:
для необратимых процессов и
для обратимых процессов.